一類益于捕食者的捕獲系統模型建立及定性分析

華極鑫,馮維龍,姜玉秋

(吉林師范大學 數學學院,吉林 四平 136000)

1 引言

1838年P.F.Verhulst[1]提出震撼生物數學界的Logistic方程后，引起了人們對生物種群數量和結構的變化探索的高潮，隨后刻畫種群間的相互作用的模型也不斷涌現.1963年 Rosenzweig和MacArthur提出反映捕食者捕獲能力強弱的功能性反應函數是雙曲線的Rosenzweig-MacArthur[2]模型，更加貼近了生態種群相互作用的真實狀態.但是前人在建立模型時沒有將捕食者種群的自身密度限制體現出來，直到1974年，Bazykin參考Rosenzweig-MacArthur模型，在此基礎上添加了密度制約項，建立了Bazykin模型[2]：

(1)

Bazykin模型更好了描述了捕食者種群的自身密度制約[3]，更好的完善了種群間相互作用模型.其中N(t)和P(t)分別為tt時刻食餌和捕食者種群的數量；r為食餌在自然狀態下的內稟增長率；K為環境能容納此種群個體的最大數量；c為捕食者對食餌的搜尋相遇的幾率；χ為捕食者吃掉食餌后的能量轉化率；δ'0代表沒有食餌情況下捕食者的死亡率；δ'1代表捕食者自我密度制約的系數；d為度量捕食者對食餌需求程度的標準，體現出捕食者對食餌的需求程度，捕食者對食餌需求越大，d反而越小.

如果在捕食者食餌生存的小生境D中產生對捕食者有利的因素，增大了捕食者與食餌的相遇幾率[4]和捕獲食餌的幾率(例如，人們大量砍伐森林，讓食餌沒有躲藏之處，捕食者更容易的發現捕獲食餌)等，捕食者的死亡率和密度制約系數也都隨之改變，假設模型在沒有食餌情況下捕食者的死亡率和自我密度制約的系數比值不變，據此建立模型：

(2)

系統(2)中e為對捕食者有利程度的系數；δ0為捕食者有利情況下沒有食餌時死亡率；δ1為捕食者有利情況下的密度制約系數.加上對捕食者有利的因素后捕食者在平衡點的數量就會大于不加有利因素時捕食者的數量，這樣也保證了捕食者在不能預計和不能克服的自然狀況下不至于滅絕.下面本文將對系統(2)的穩定性態詳細分析.

2 系統分析

為下文方便，我們用下列記號：

(i)考慮到實際生物學意義，我們在D={(N，P)|N≥0,p≥0}上研究系統(2).

令

(3)

定理1 系統(2)在區域D上沒有閉軌線.

證明 選取Dulac函數B(N,P)=N-1P-1,由計算得

由Dulac判據知，系統(2)在區域D內不存在閉軌線.

定理2 系統(2)的平衡點ο(0,0)是鞍點.

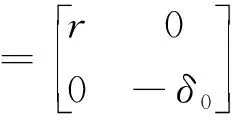
定理3KN0時，E(K,0)是鞍點.

.

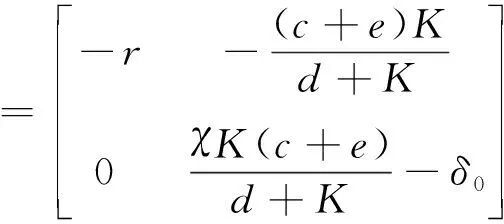
當K0,β>0，故E(K,0)是穩定結點；當K>N0時，有β<0，故E(K,0)是鞍點.

定理4K>N0時，系統(2)存在唯一的正平衡點E'(N*,P*)，并且是局部穩定的.

證明 先證明E'(N*,P*)的存在性和唯一性.即f1(N,P)=0和f2(N,P)=0有交點.

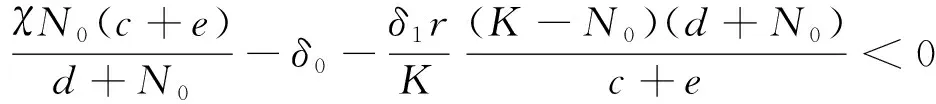
由零點定理知存在N0≤N*≤K,使F(N*)=0,即存在正平衡點E'(N*,P*).因h(N)是關于N的遞增函數，故在[N0-1,K+1]上存在唯一的N*,從而E'(N*,P*)唯一.

下證E'(N*,P*)是局部穩定的.

有

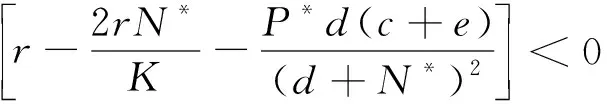
故有α>0，β>0,因此E'(N*,P*)是局部漸近穩定的.

3 生物意義

根據系統(2)，在有利于捕食者捕獲食餌的情況下，捕食者在平衡點的數量P*會比不加有利因素時的捕食者數量大.對于瀕臨滅絕[5]危機的捕食者種群來說，我們可以人工進行輔助，給予捕食者有利的生存條件，增加捕食者與食餌的相遇機會和捕獲機會，這樣能保證捕食者在有其它突發自然狀況下不至于滅絕，而且能使稀珍品種的捕食者繁殖壯大，有害無益的食餌繁殖得到控制，直到捕食者和食餌數量分別達到P*，N*時，兩種群相互作用達到平衡狀態.系統(2)的建立，可以指導人們解決和緩解在實際生態中種群滅絕的問題，從而達到保護珍稀物種，抑制那些大量繁殖而又對人們無益處的種群的目的，實現生態平衡穩定.

參考文獻：

[1]馬知恩.種群生態學的數學建模與研究[M].合肥:安徽教育出版社,1996.

[2]Peter Turchin.Complex population dynamics:Generalized Lotka-Volterra Models[J].Princeton university press,2003:94-99.

[3]馬知恩,周義倉.常微分方程定性與穩定性理論[M].北京:科學出版社,2001.

[4]姜玉秋.Turchin-Batzli捕食者-食餌系統的定性分析[J].東北師大學報,2006,38(4):17-21.

[5]尚玉昌.普通生態學[M].北京:北京大學出版社,2002.