微積分習題課的范例教學法

吳世玕，杜紅霞

(1.江西理工大學 理學院，江西 贛州 341000；2.江西理工大學 機電學院，江西 贛州 341000)

1 范例教學法概述

“范例教學”，又稱“示范方式教學”.瓦根舍因認為，范例就是“隱含著本質因素、根本因素、基礎因素的典型事例”[1-2].范例教學主張，在有限的教學時間內，組織學生進行“教養性學習”，讓學習者從選擇出來的有限的例子中主動地獲得一般的、本質的、結構性的、原創性的、典型的以及規律性的跨學科的東西.

范例教學的目標就是要達到四個統一：教學和訓育的統一，問題解決學習與系統學習的統一，掌握知識與培養能力的統一，主體與客體的統一.

范例教學認為，為了培養學生獨立性，教學必須以學生為方向，從學生實際出發，牢牢地把學生的興趣與關心的問題緊扣在一起.要幫助學生去發現，去追求新知識、新技能.

在教學內容上，選擇教學材料，要注意“基本性”，“基礎性”和“范例性”.在教學過程方面，主張通過對典型個例的學習，抓住事物的本質.將個別抽象為類型，用范例理解類型的規律，范例性地獲得有關經驗.在教學方法上，范例教學模式與發現教學模式[3]、研究式教學模式[4]相結合，效果會更好.

2 選擇例題要注意“基礎性”

習題課是為了讓學生在教師的引導下，復習課本上的基本理論、基本方法.關鍵在于引導，而不是題海戰術.精選一些有代表性的問題，通過一題多解的方法，培養學生發散思維，將學生所學的知識、方法串聯起來.所選例題，要能從多方面反映所學知識和方法，而且有推廣的價值.還要讓學生來評論，什么方法更簡捷，更精彩，以達到從眾多解法當中，尋找最優解法，培養學生集中思維和綜合分析能力.

比如，在高等數學上冊期末復習：求極限，求導數，求積分時，通過一些典型例題，來達到對這3方面的訓練.先讓學生回憶，在求極限方面，學過哪些方法，然后，通過典型例題，復習、訓練求極限的方法.

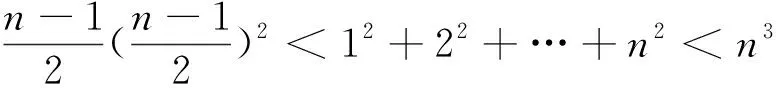
解法2 學生已經學習了數列極限的夾逼準則，教師在課堂上，啟發學生將這個數列適當放大、縮小，就可將極限求出.

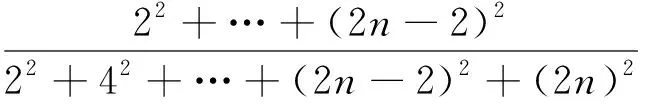
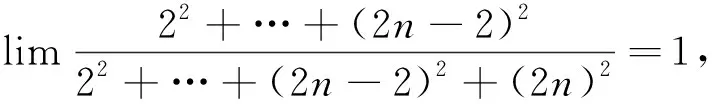
解法3 對于函數極限，學生已經學過羅必達法則.對于數列極限，是否也有類似的定理或法則，為了拓寬學生的知識面，可以分析這個數列，分母是單調遞增的正無窮大數列.同時向學生介紹施圖茲定理，用來求解這種極限，非常容易.

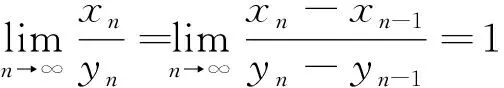
解法4 定積分是黎曼積分和的極限，在處理和的極限時，常想到定積分.本例分子、分母都是和的形式，可否將分子、分母化成黎曼積分和的形式？黎曼積分和中都有f(ξi)Δxi的形式.本例如何找f(ξi)和Δxi.

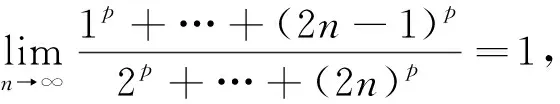
綜上，我們通過這個典型例題，培養了學生觀察問題的能力，由p=2時的極限等于1可知，p>0時，也可用定積分方法，得出極限為1的結論.

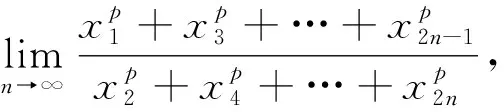
在微積分的學習中，有很多典型例題，教師要善于挖掘、利用.利用典型例題，進行數學思想、數學方法的教學，可以事半功倍.通過教師講解上述例題，引導學生復習了求極限的一些經典方法.

3 選擇例題要注意“基礎性”

在微積分的學習中，有很多經典問題處理方法相似.教師可以通過典型例題，精講其方法，并將其推廣到類似問題上，讓學生學會學習，舉一反三，觸類旁通.所選例題要能反映基礎知識、基本方法.

以多元函數的積分學為例，包括二重積分、三重積分、第一型曲線積分、第二型曲線積分、第一型曲面積分、第二型曲面積分，這些積分可以相互轉化.在復習積分方法及應用時，教師可精講典型例題，再告知學生如何類推到類似問題上.所以選擇例題時要具有“基礎性”，訓練學生計算的基本功.

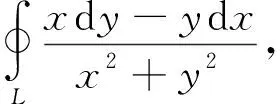
這是一個經典的例題，很多微積分教材上都有.若閉曲線包圍原點，其解法是“挖洞法”.將沿的積分，化成沿“洞”的邊界上的積分.在“洞”的邊界上，被積函數的分母是常數，可以將其提到積分符號外，從而達到簡化積分的效果.

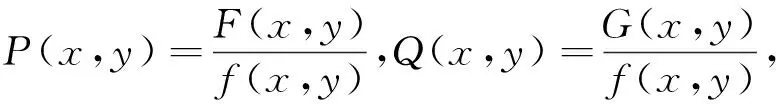
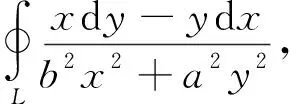
曲線積分、曲面積分的計算中，補線(補面)法、挖洞法，所依賴的分別是格林公式和高斯公式.復習課時，教師通過對典型例題的講解，可以起到以點帶面的作用.多元函數積分的應用，也可以用典型例題，說明方法和計算技巧.比如，二重積分中，可用質心公式計算一些二重積分，可將此方法類推到三重積分、第一型曲線積分、第一型曲面積分.教會學生歸納、總結、舉一反三、觸類旁通，真正達到教學目的.

4 選擇例題要有“范例性”

在微積分教學中，對典型問題的剖析，要從多方面解釋，潛移默化地培養學生學會全面思考問題.教師在平時備課時，要多花精力，準備這樣的典型例題.尤其在復習、總結課上，從不同角度剖析同一問題，學生獲得的不僅僅是知識、數學方法，更多地是獲得分析問題、處理問題的一般方法，從范例中獲得有關經驗.

例3 求y=arctanx在x=0點的n階導數.

很多高等數學或數學分析教材上都有這個習題，有一定的難度，都是放在求高階導數的練習題中，訓練兩個函數乘積的n階導數的萊布尼茲公式.其實，這個題目，可以從多方面來分析，以達到不同的訓練目的和作用.

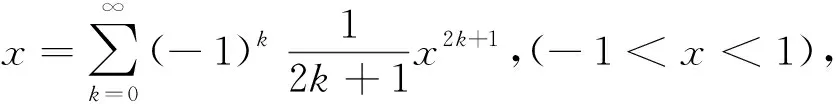
通過一個典型例題，可以復習多方面的知識和方法.學生體會到了看問題和分析問題，要從多方面考慮，這樣才能更全面、更準確地把握問題的實質.

參考文獻：

[1]李濤.“范例教學”理論的現代教學特征[J].教學與管理,2007(6):10-12.

[2]顧明遠,孟繁華.范例教學:舉一隅以三隅反[J].教育理論與實踐,2008(5):33-34.

[3]徐繼存,趙昌木.現代教學論基礎[M].北京:北京大學出版社,2008.

[4]陳鼎興.數學思維與方法-研究式教學[M].南京:東南大學出版社,2008.