SPSS軟件在電量需求預測中的應用

杜玉霞,梁 武,俞亭亭

(宿州學院 數學與統計學院,安徽 宿州 234000)

SPSS[1-2]統計軟件是使用最為普遍的統計軟件之一，它是由數據錄入、資料編輯、數據管理、統計分析、報表制作、圖形繪作為一個整體，具有強大的數據管理和分析功能，支持多種統計圖表的結果輸出.目前，SPSS廣泛應用于特定區域的銷售分析、市場營銷、統計、社會經濟調查、企業管理、教學和行政管理等領域. 本文運用SPSS軟件對西北電網電量需求進行外推預測，取得了較高的預測精度.

1 時間序列ARIMA(p,d,q)模型

ARIMA(Autoregressive Integrated Moving Average)模型全稱差分自回歸移動平均模型，是由博克斯(BOX)和詹金斯(Jenkins)于20世紀70年代初提出的一種著名的時間序列預測方法，又稱為B-J模型.它的一般形式為：ARIMA(p,d,0)，其中p是自回歸模型的階數，d為時間序列成為平穩時所做的差分次數，q是移動平均的階數.ARIMA方法能夠在對數據模式未知的情況下找到適合數據所考察的模型，在醫學等很多方面得到了廣泛應用[3-4].其建模思想是將預測對象隨時間推移而形成的數據序列視為一個隨機序列,用一定的數學模型來近似描述這個序列,并從時間序列的過去值及現在值來預測未來值.通過對模型的分析與研究，能夠從本質上認識時間序列的結構與特征,達到最小方差意義下的最優預測.

2 電量需求的ARIMA(p,d,0)模型

以下就2005.1-2006.12西北電網電量需求數據(見表1)，建立電量需求的ARIMA(p,d,q)模型. 繪制電量需求數據時序圖(見圖1).通過觀察圖1，可以看出數據呈現周期波動，并且存在明顯的遞增趨勢.運行SPSS軟件得到原始數據的自相關系數和自相關圖，見表2、圖2.

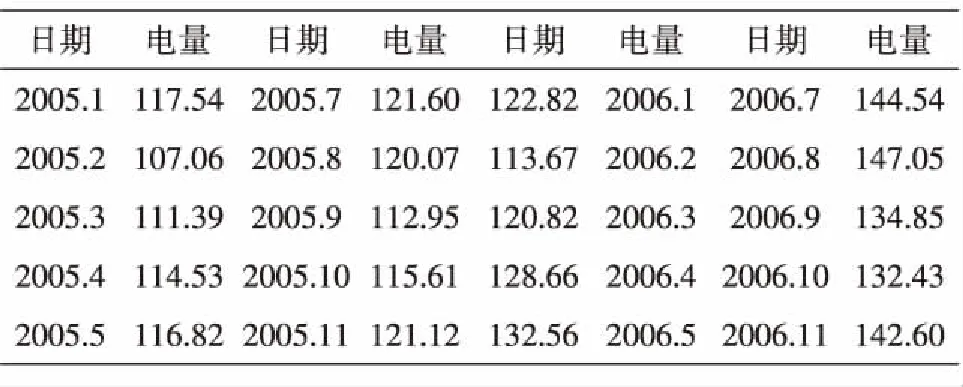
表1 2005.1-2006.12 西北電網電量需求 單位:億千瓦時

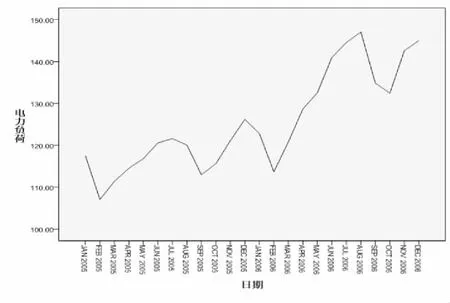
圖1 2005-2006年電力負荷時間序列數據序列圖

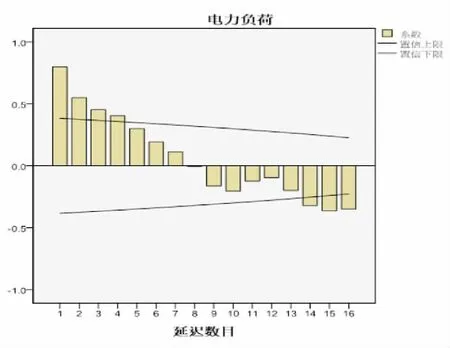
圖2 自相關圖

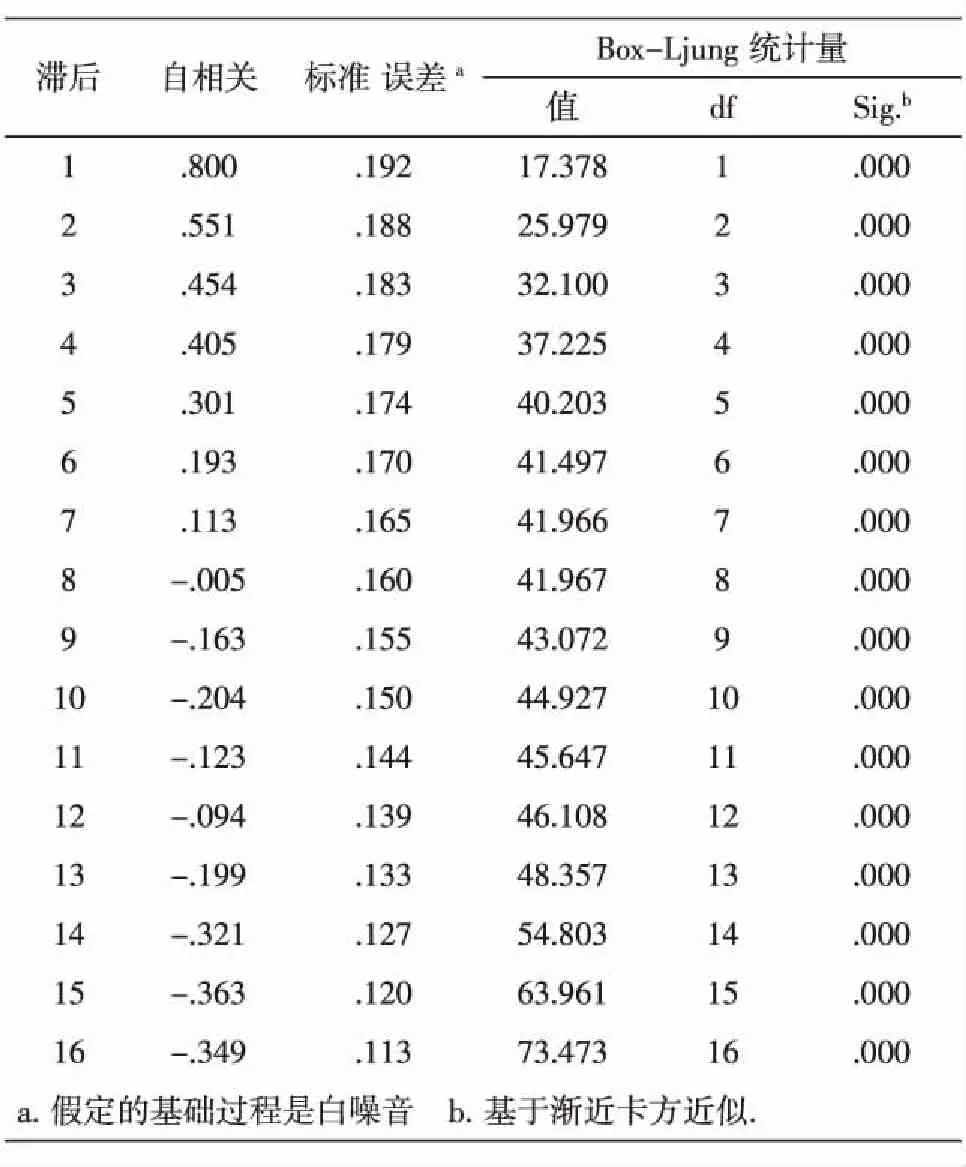
表2 自相關系數

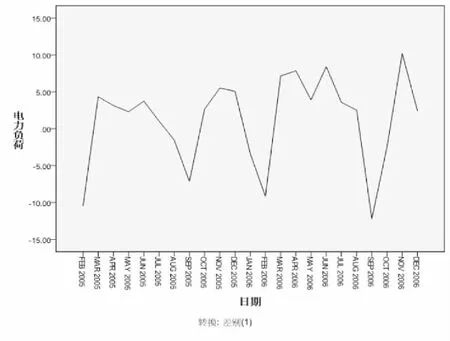
圖3 一階差分的時序圖

圖4 一階差分后自相關圖

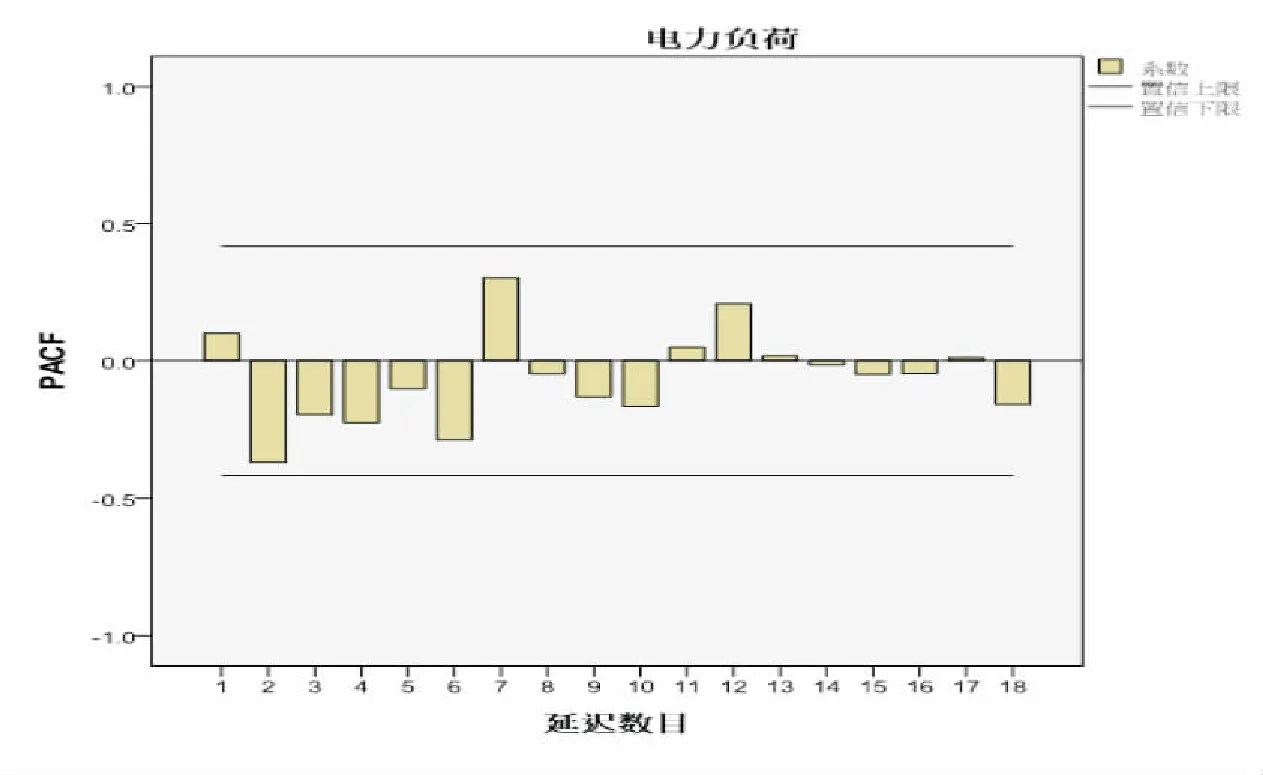
圖5 一階差分偏相關圖

圖6 ARIMA模型殘差的相關函數圖

由圖2和表2可以看出該序列延遲了4階后，相關系數衰減到接近0，然后又出現了較大的負相關.這表明該序列具有顯著單調遞增的趨勢.所以我們需要利用差分的方法對原序列進行變換，剔除長期趨勢使得序列變得平穩.進行1階差分得時序圖3,自相關圖4，偏相關圖5.

觀察圖3可以看出一階差分后長期趨勢基本上從序列中剔除，原序列變換成了平穩時間序列，差分階數d=1,觀察圖4、5可以斷定p=1,q=0，確定西北電網電量需求的時間序列模型為ARIMA(1,1,0).

3 對ARIMA(1,1,0)模型進行檢驗

對于西北電網電量需求的ARIMA(1,1,0)模型，運行SPSS軟件得模型參數見表3，殘差的相關函數圖見圖6，模型統計量見表4.

表3 ARIMA 模型參數

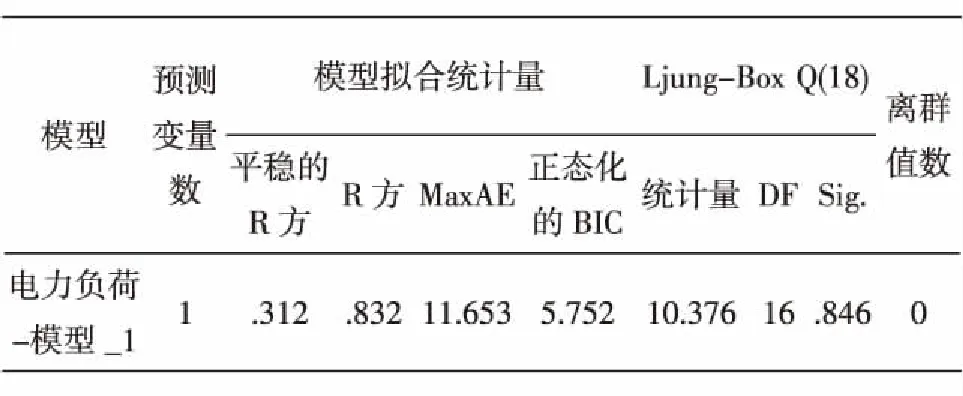
表4 模型統計量

從表3可以看出t統計量的值遠小于0.05，表明此模型一階自回歸系數顯著.由圖6可以看出兩個圖形都沒有顯著的趨勢特征(拖尾或截尾)，且殘差序列的自相關和偏自相關系數大多接近于零，這表明殘差序列已經達到白噪聲，模型與數據擬合的較好.

由表4模型統計量中R方上來看，擬合優度也達到了0.832，sig值為0.846遠大于0.05，這說明了構建的ARIMA(1,1,0)模型的擬合效果良好，可以用來預測西北電網電量.

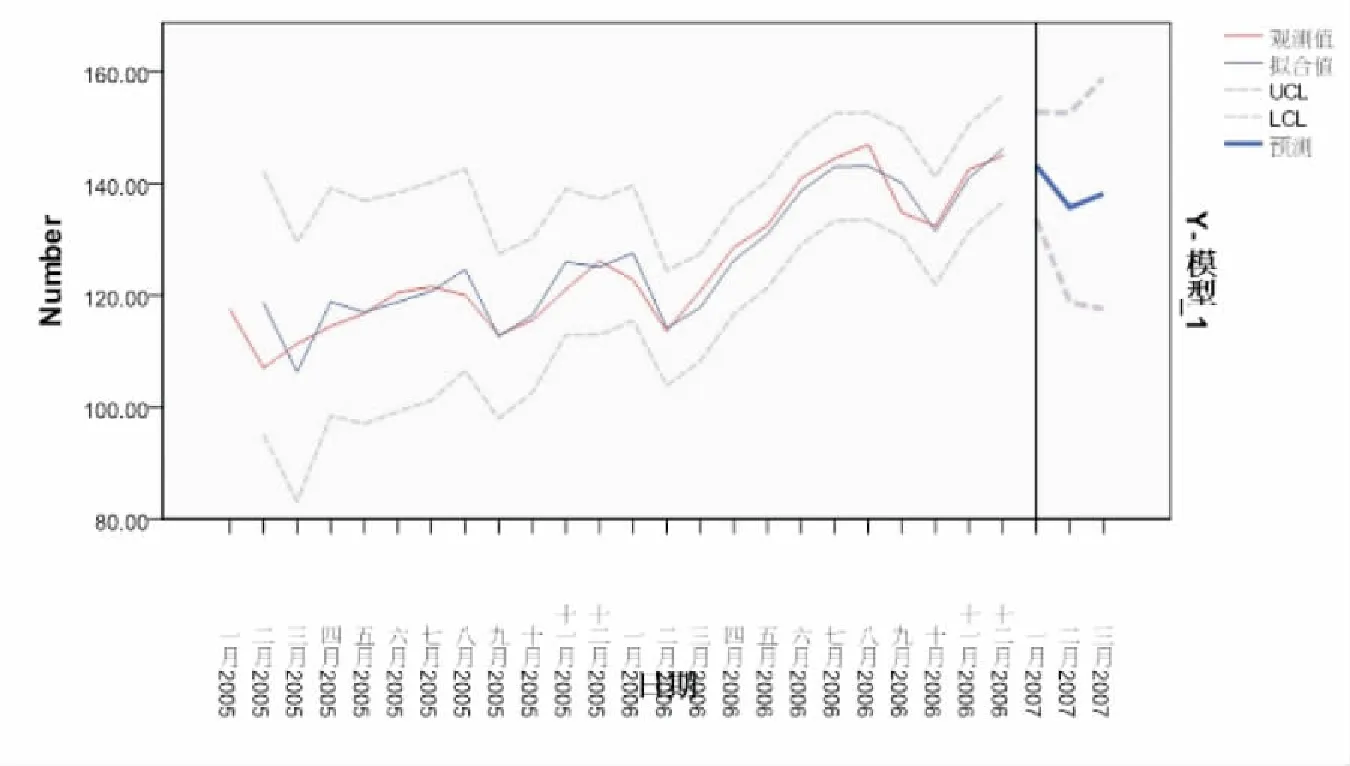
圖7 預測的擬合結果

4 運用ARIMA(1,1,0)模型進行預測

運行SPSS軟件，得擬合結果見圖7，從圖7預測的擬合曲線圖可以直觀的看出ARIMA(1,1,0)模型很好的擬合了原序列.運用該模型進行外推預測得2007.1-2007.3的預測結果見表5.

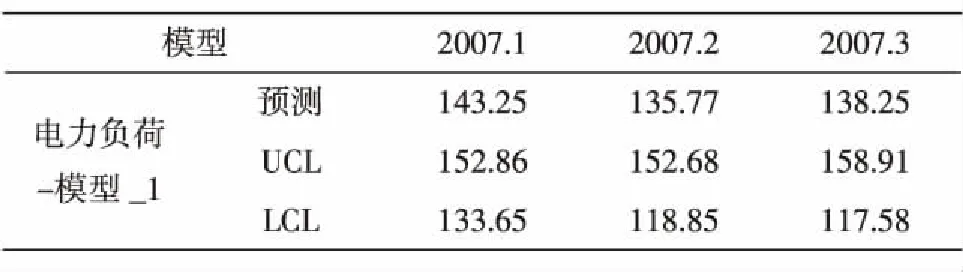
表5 預測結果

5 結語

參考文獻：

[1]郭志剛.社會統計分析方法—SPSS軟件應用[M].北京:中國人民大學出版社,1999.

[2]李志輝,羅平.SPSS for Windows統計分析教程[M].北京:電子工業出版社,2006.

[3]周水森.ARIMA模型在瘧疾發病預測中的應用[J].中國原生物學雜志,2007,2(4):284-286.

[4]吳家兵,葉臨湘,尤爾科.ARIMA模型在傳染病發病率預測中的應用[J].數理醫藥學雜志,2007,20(1):90-92.