雙錐鎖緊盤傳遞扭矩分析

佟占勝，周景龍，袁志剛

(1.中國重型機械研究院股份公司，陜西 西安 710032;2.中國重型機械有限公司，北京 100036;3.首鋼長白結晶器有限責任公司，河北 秦皇島 066311)

0 前言

鎖緊盤是一種軸和轂之間廣泛采用的無鍵聯接裝置。鎖緊盤是由帶有錐度角的外套與內套組成，通過螺栓從外部對軸套施加預緊力，內套被壓縮，使工作機主軸與減速機輸出軸緊密結合，通過過盈配合達到傳遞扭矩要求。鎖緊盤廣泛應用于建材、風電及運輸等行業。在相同軸徑條件下，較之鍵連接，采用鎖緊盤連接方式能傳遞更大的扭矩。鎖緊盤連接易于檢修，檢修時只需卸下螺栓，內外套自然松開，工作機主軸與減速機輸出軸間隙恢復，實現輕松分離。

1 鎖緊盤設計流程

鎖緊盤有兩種類型，單錐與雙錐形式，雙錐鎖緊盤的結構如圖1所示。

鎖緊盤的選定方法、安裝、防護與拆卸，按照JB/ZQ4194-2006執行。值得注意的是鎖緊盤錐度角設計，已知錐面傳遞扭矩計算公式為

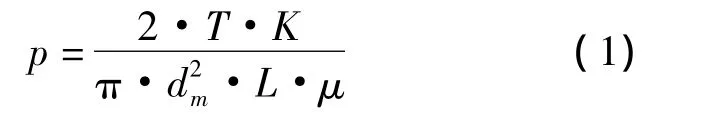
式中，P為工作壓力;T·K為傳遞的最大扭矩值;dm為接觸工作面直徑;L為工作長度。

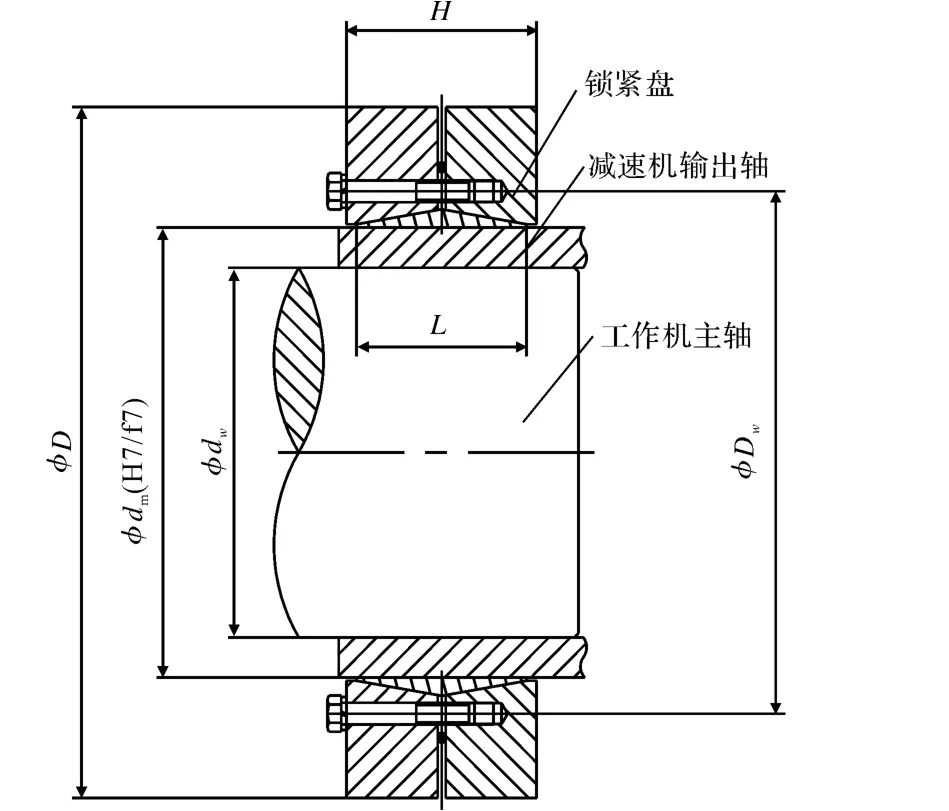
圖1 雙錐鎖緊盤結構圖Fig.1 Structure of double-taper lock disc

應用式(1)設計鎖緊盤應該注意兩個問題，一是將T·K作為額定負荷最大轉矩;二是注意摩擦系數μ與錐度角α的關系。

摩擦系數的選取以及測定十分重要，不但決定著結合面徑向壓力大小，而且與錐度角關系緊密相連，如果錐度角正切值小于摩擦系數，即tanα≤μ。當螺栓拆除，去掉外力后，鎖緊盤會發生自鎖，需要對鎖緊盤施加相反的力才能使內外套分開。因此設計鎖緊盤時，要根據工作工況，合理計算摩擦系數以及是否需要自鎖存在。降低摩擦系數時可以選擇在錐形工作面上涂潤滑油，增大摩擦系數則可以在錐形工作面上加減摩劑。

減速機輸出軸與工作機主軸之間的理論計算可以參考文獻［5］，在此不再贅述。

文獻［2］目錄中所列的額定扭矩值與額定軸向載荷值是按照鎖緊盤所能傳遞的最大值列出的，不含安全系數，校核時，應考慮起動和沖擊載荷。

2 鎖緊盤有限元分析

有限元分析技術能夠模擬真實的自然現象，解決從簡單到復雜的工程實際問題，在越來越多的行業領域得到廣泛應用。本文使用Hypermesh與Msc.marc聯合仿真方法對雙錐鎖緊盤進行分析。

鎖緊盤的有限元分析，根據其結構可以簡化為軸對稱問題，其特點是物體為某一平面繞其中心軸旋轉而形成的回轉體。由于鎖緊盤涉及到多個軸對稱旋轉體以及接觸問題，用彈性力學的解析方法進行應力計算較復雜，很難得到精確解，因此采用有限元法進行應力分析，在工程上十分必要，同時用有限元計算得到的數值解，近似程度也很高。

2.1 網格劃分

自由網格劃分對于處理結構網格劃分是最快的，但是有其缺點，首先可能會出現單元粘結，無法求解;其次由于網格單元長度一樣，單元數量較多，求解時間長。使用Hypermesh進行手動與自由網格劃分結合方法，能使接觸區域網格密集，有助于得到精確數值解，遠離接觸區域的部分，經過處理，網格單元較大，不僅節省計算時間，節約計算資源，而且能得到同樣精確的數值解。本文采用四節點平面網格。圖2為劃分好的鎖緊盤工作結構網格圖。

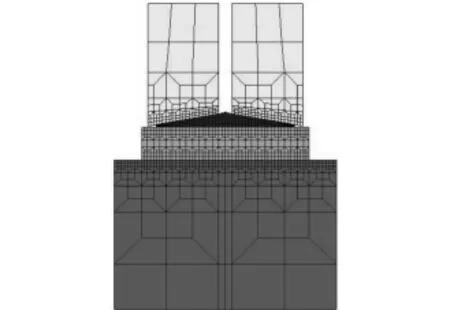
圖2 鎖緊盤網格圖Fig.2 Finite element grid of lock disc

2.2 邊界條件處理

鎖緊盤結構既是軸對稱旋轉體，也是沿中間截面對稱的。因此可以將中間截面做全約束處理，假設載荷均勻分布，不會發生偏移。

由于采用螺栓預緊力加載處理，有許多不確定因素，包括螺紋的加工精度，內外環的摩擦系數等。所以對外套使用位移載荷，最終也是通過確定過盈量計算傳遞扭矩更為方便。經過有限元分析后，通過外套位移加載值與減速機輸出軸與工作機主軸表面徑向壓力的關系，找到能夠傳遞扭矩的合適鎖緊盤外套軸向位移量。在此工況下得到鎖緊盤變形值與應力值，以確定鎖緊盤材料是否滿足設計要求。這樣更符合實際。

2.3 鎖緊盤材料與性能

為了確保鎖緊盤性能，鎖緊盤外套使用材料42CrMoA，鎖緊盤內套使用40CrA，調質處理。表1為材料力學性能參數。采用不同材料可以預防鎖緊盤在高壓載荷工況下，外套與內套發生粘接，同時也滿足傳遞扭矩和實際工況。

表1 Q235-A鋼材力學性能表Tab.1 Mechanical properties of Q235-A steel

2.4 鎖緊盤有限元分析結果

鎖緊盤是目前輥壓機輥子主軸與減速機輸出空心軸采用的連接方式。某900 kW輥壓機配套的減速機傳遞扭矩750 kN·m，采用雙錐鎖緊盤型號SP2-560×940，此鎖緊盤額定轉矩2 130 kN·m，軸向力9 261 kN，安全系數達到2.8。

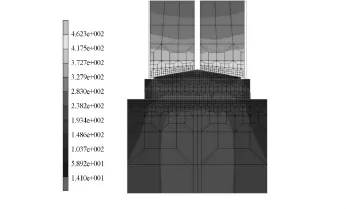
圖3 鎖緊盤結構應力圖Fig.3 Stress diagram of lock disc

圖4 鎖緊盤結構徑向Y位移圖Fig.4 Y-radial displacement of lock disc

利用Msc.marc軟件對鎖緊盤型號SP2-560×940模型有限元分析計算，得到鎖緊盤應力和位移云圖如圖3、圖4所示。根據圖3、4得到當鎖緊盤傳遞最大扭矩時，最大應力為462.3 MPa，最大徑向位移為0.459 1 mm，其中內套最大等效應力如圖5所示，最大應力為384.2 MPa。

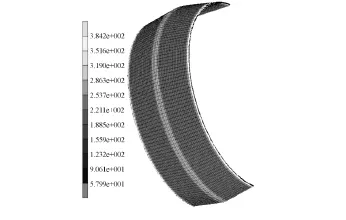
圖5 鎖緊盤內套應力圖Fig.5 Stress diagram of inner sleeve of lock disc

鎖緊盤在滿足傳遞2 130 kN·m扭矩時，承受的應力值較大，但是沒有超過材料的屈服極限。而實際加工的鎖緊盤外套是有采取打磨圓角的辦法來降低應力集中的。

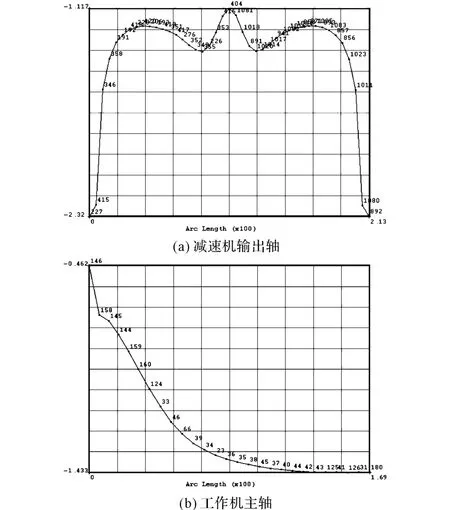
圖6 減速機輸出軸和工作機主軸的徑向應力分布圖Fig.6 Radical stress distribution of the output shaft of reducer and the main shaft of operating machine

根據圖6a與圖6b，可以提取出各個節點徑向應力，進而求得接觸面上徑向應力平均值。

根據式(1)計算得到工作機主軸與減速機輸出軸連接能夠滿足傳遞扭矩。

從圖6a可知減速機輸出軸上所受到的徑向應力并不是均勻分布的，在接觸兩端應力較大。而又由于外套處于工作狀態時，并沒有完全接觸，所以靠近中間截面的徑向應力最小。圖6b為鎖緊盤沿中間截面對稱結構，從圖中可知工作機主軸輸出徑向應力由于受到減速機輸出軸壓縮作用，中間壓縮量最大，過盈量大，徑向應力值最大;而兩端壓縮小，過盈量小，徑向應力相對較小。

圖7為間隙消除問題。通過圖7a可知，由于鎖緊盤內套與減速機輸出軸接觸，致使減速機輸出軸等高線顏色表發生變化。當鎖緊盤外套軸向位移0.3 mm時，鎖緊盤內套與減速機輸出軸間隙消除，減速機輸出軸發生徑向位移值7.763e－3 mm。

圖7 間隙消除時的位移圖Fig.7 Displacement at the clearance disappearing

通過圖7b可知，由于減速機輸出軸與工作機主軸接觸，致使工作機主軸等高線顏色表發生變化。當鎖緊盤外套軸向位移0.4 mm時，減速機輸出軸與工作機主軸間隙消除，工作機主軸發生徑向位移值1.71e－3 mm。

文獻［2］目錄中，已知鎖緊盤型號SP2-560×940額定負荷時，螺栓預緊力矩1 210 N·m，螺栓規格 M27×180，已知有螺栓預緊力計算公式

式中，摩擦系數μ=0.15、螺栓預緊力矩F=239 012 N;螺栓直徑d=27 mm。

通過有限元計算，滿足傳遞最大扭距時，鎖緊盤錐形面所受到的軸向力與徑向力如圖8所示。

圖8 鎖緊盤錐面受力數值圖Fig.8 Force on taper of lock disc

圖8數據顯示鎖緊盤錐形面軸向受力平均值223 248 N，與理論計算數值接近。

鎖緊盤在滿足傳遞扭矩工作條件下，錐度角大小與鎖緊盤軸向位移關系密切相連。計算不同錐度角與鎖緊盤外套軸向位移的關系見表2。

表2 鎖緊盤錐度角α與外套軸向位移關系Tab.2 Relationship between the taper angle α of lock disc and the axial displacement of outer sleeve

根據表2繪制圖9，從中可知，在滿足傳遞扭矩條件下，錐度角越小，所需的軸向行程就越大。當角度越小，位移行程趨勢越大，這也符合沒有錐度角，無法傳遞扭矩的原理。

因此具體的錐度角要根據實際情況來設計。需要考慮是否有足夠的軸向空間容納軸向行程以及是否需要自鎖和摩擦系數等。

鎖緊盤與漲套設計原理一致，很多設計者認為鎖緊盤外套外圈直徑很大，可以減小外圈直徑值。通過有限元分析，認為這種理念是錯誤的。表3列出了當外套軸向位移為3.6 mm時，在不同鎖緊盤外套外圈直徑D條件下，產生的壓力P，以及實現傳遞最大扭矩時軸向位移值X和鎖緊盤外套等效應力值σ。

圖9 錐度角與軸向位移關系圖Fig.9 Relationship between taper angle and axial displacement

表3 鎖緊盤外套外圈直徑D對應力的影響Tab.3 Impact of diameter of outer ring of outer sleeve on stress

從表3中可知，鎖緊盤外圈直徑對整體設計影響較大。而漲套的外圈直徑很小，是因為漲套外圈還要與其它零件相連，漲套是用外徑擴張來保證傳遞扭矩，這是其與鎖緊盤的重要區別。

3 結論

(1)分析結果說明鎖緊盤在傳遞最大扭矩工況下，所受到的最大等效應力并沒有超過材料的屈服極限。文獻［2］中提到鎖緊盤外套與內套材料可以使用屈服強度大于360 MPa的鋼或鑄鋼，結合其他文獻與本文分析，作者認為這一數據不太合適。

(2)鎖緊盤內套與減速機輸出軸，以及減速機輸出軸與工作機主軸之間的徑向應力并不是固定值或是呈線性分布。

(3)通過螺栓預緊鎖緊盤時，軸向行程0.4 mm內，是為了消除間隙，減速機輸出軸與工作機主軸并沒有產生徑向應力。

(4)鎖緊盤錐度角設計時，為了不產生自鎖，應該保證tanα≥u，即錐度角正切值大于摩擦系數，更要根據空間與軸向位移實際情況設計錐度角。

(5)鎖緊盤的設計不要省外圈材料，通過有限元仿真說明，外圈直徑大小關乎整個結構設計是否合理，是否可以使用。

(6)鎖緊盤的理論計算數據龐大，過程繁瑣，使用有限元方法，可以很方便的得到其數值解，并且易于優化。

［1］陶德峰，王建梅，黃訊杰，等.風電鎖緊盤軸套位移與應力計算［J］.太原科技大學學報，2012，33(1):40－44.

［2］梁嫣麗，寇毅.風電鎖緊盤工藝設計［J］.現代工業設計和信息化，2012(7):47－48.

［3］JB/ZQ4194－2006.鎖緊盤［S］.

［4］閆登華，宋毅勇.鎖緊盤在地面纜車驅動設備中的應用及計算［J］.起重運輸機械，2013(2):104－106.

［5］陳火紅，楊劍，薛小香，等.新編Marc有限元實例教程［M］.機械工業出版社，2007.

［6］GB/T 5371－2004.極限與配合，過盈配合的計算和選用［S］.

［7］王顏輝，郭強.鎖緊盤傳遞扭矩有限元分析計算［J］.中國科技縱橫，2013(21):47－49.

［8］王鈺棟，金磊，洪清泉，等.Hypermesh應用技巧與高級實例［M］.北京:機械工業出版社，2013.