基于奈特不確定性的ICAPM研究

周碎倫

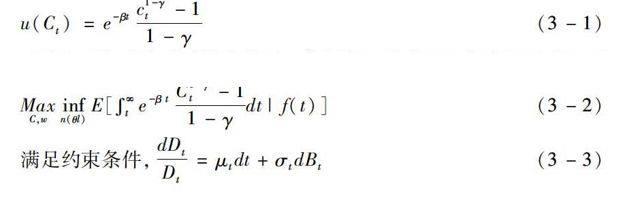
摘 要：現實的資本市場信息是不完全的，投資者在投資決策過程中必須承擔信息不完全所帶來的奈特不確定性。本文將這種不確定性作為定價因子考慮，在一般均衡框架下，假設未來資產紅利是一個不可觀測的狀態變量，服從隱馬爾科夫過程，利用隨機貼現因子法重新求得擴展的ICAPM模型。

關鍵詞：奈特不確定；隱馬爾科夫；ICAPM

一、引言

在現實中，由于信息不對稱和投資者自身因素限制，投資者在進行投資決策時并不知道這些參數的真實值，而只能利用各種可獲得的信息對這些參數進行估計，再基于估計值進行投資決策。在這種情況下，投資者將面臨著一種與風險相區別的不確定性，那就是奈特不確定性，即投資者并不知道金融變量的未來分布，或即使知道分布但也不能準確的知道分布的各個參數。在這種不確定下，投資者通過資產定價模型所得到的結果本身具有不確定性，如由參數估計風險所帶來的參數不確定性。既然投資者在不完全信息下承擔了奈特不確定性，那么在不確定厭惡的假設條件下，就必然要求獲得相應的補償，由不完全信息所造成的奈特不確定性可能是一個定價因子，應該被定價。

目前學術界對奈特不確定性的研究主要關注參數不確定下的投資組合選擇問題，而較少將其作為定價因子進行研究。實際上這類研究的本質是把一個未知的客觀分布轉換成一個已知的主觀分布來研究，把一個奈特不確定性問題轉化成風險問題，還是屬于風險領域的研究，隱含假設對任何的不確定性，投資者都能給出唯一的主觀概率。……