無疑處生疑 有疑處釋疑——國優課“二次函數的概念”教學片斷賞析與思考

唐 芬，朱德全

?

無疑處生疑 有疑處釋疑——國優課“二次函數的概念”教學片斷賞析與思考

唐 芬1，朱德全2

（1．重慶市永川中學，重慶 永川 402160；2．西南大學 教育學部，重慶 400715）

學生數學學習的過程是“無疑—有疑—無疑”的循環和超越過程．有疑和無疑是一對矛盾．教師的作用是“教”有疑與“教”無疑：無疑者需“教”而有疑，即無疑處生疑；有疑者又應“教”而無疑，即有疑處釋疑．這便是“教”有疑與“教”無疑的辨證處理要訣，也是“教”有疑和“教”無疑的理想境界．

有疑；無疑；問題；概念教學；二次函數

問題是數學的心臟．因此，為問題而教，是數學教學的出發點和著眼點．數學是由問題構成的，教學目標需要問題來展現，教學過程需要問題來活化，教學對象需要問題來觸動．離開問題，數學教學僅定位于單向的靜態的傳輸系統．可見，問題應是數學教學的邏輯起點，問題和問題解決是數學教學的生長點[1]．古人說：“學起于思，思源于疑．”有疑才有問，有問才有思，有思才有得．疑問是思維的火種，思維以疑問為起點．南宋理學家朱熹說：“讀書無疑者，須教有疑；有疑者，卻要無疑，到這里方是長進．”[2]這說明“有疑”和“無疑”是一對矛盾：無疑者，需“教”而有疑，即無疑處生疑；有疑者，又應“教”而無疑，即有疑處釋疑．

目前，數學課程改革己進入“后課改時代”，但數學教學中仍普遍存在“缺乏問題意識，重結果輕過程，掐頭去尾取中段，在數學對象的背景、引入、形成上著墨不夠，導致數學對象的學習過程被濃縮”等“去問題化”現象[3]，這不利于學生創新精神的培養和數學素養的提高．數學課堂如何為“疑”而教，回歸數學本質，做到“教有疑”與“教無疑”呢? 這不論是過去還是當下，也是未來數學課堂的永恒主題．這里以“國優課”（第八屆全國初中青年數學教師優質課評比一等獎課例）參賽選手王文俊老師的“二次函數的概念”為例，對“教有疑”與“教無疑”做些詮釋．研究者認為，整堂課以問題為驅動，理性自然，把“疑”貫穿教學全過程，讓學生體驗數學地建構概念、形成概念、應用概念、延伸概念，逐步學會數學地認識和解決問題．

1 概念鏈接 學似無疑

1.1 教學片斷呈現

師：八年級我們學習過函數概念，你能說說什么是函數嗎？

先后有3名學生回答并相互補充后得出較完整的函數概念，教師屏幕顯示．

追問1：你認為函數概念中有哪些關鍵詞？

追問3：我們已經學過了哪些函數？……

追問4：以一次函數為例，說說主要研究了函數的哪些內容？……

師總結：我們學習一次函數經歷了這樣的過程（順序播放圖1）：從實際問題中，找到兩個變量，如果它們存在一定的依賴關系，就得到一個函數，畫出函數圖象后，通過直觀觀察，總結出函數的性質，最終又回到實際問題．所以數學來源于生活，也必將應用于生活．今天我們還要學習一種新的函數，請看實際問題．

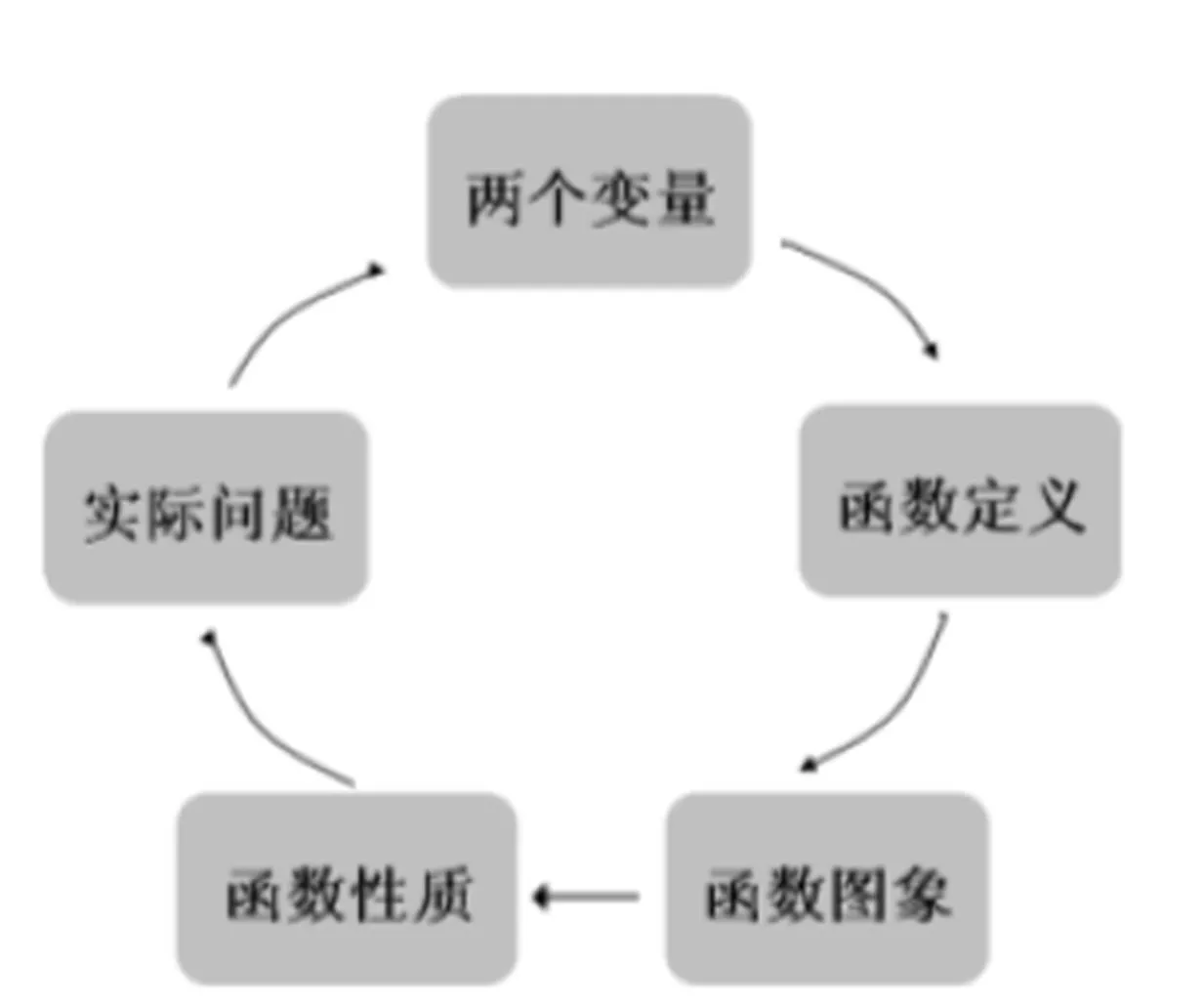
圖1

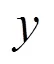
情境二：用16米長的籬笆圍成長方形的生物園飼養小兔：

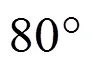
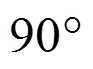
（本片段主要采用問答式，問題解決順利，其中情境五有適當點撥，教師板書6個解析式．）

1.2 評析與思考

李邦河院士認為“數學根本上是玩概念的，不是玩技巧．技巧不足道也！”蘇聯教育家克魯普斯卡婭曾說：“數學是許多概念組成的鎖鏈．”由此可見，數學是思維的體操，數學概念是數學思維的細胞，問題是數學概念的活性酵母[4]，它源自教學目標，成于情境的潛在預設．通過復習，聚焦函數概念中始終不變的屬性——“對應”[5]，幫助學生厘清了變量、函數、常量等概念系統，再現一次函數的學習過程；然后基于學生的生活現實，著眼于學生的最近發展區，逐級而上地提出5個情境問題，為學生創設直覺思維場情境[6]，學生順利完成，沒有疑點和錯點．盡管學生看似無疑，但教者實屬有意：前面的復習既是本章的導學，也為“通過類比探究二次函數”提供了認知基礎；后面5個情境問題是執教者對教材的整合，教材的情境問題只有二次函數模型，執教者增加了一次函數、反比例函數、無理函數模型，然后引導學生從眾多的模型中抽象出二次函數的特征．如何抽象？其特征是什么？問題亦蘊藏于預設的邏輯情境中．

2 概念建構 貴在生疑

2.1 教學片斷呈現

師：同學們，請觀察剛才列出的6個關系式，它們都是函數嗎？

生齊答：是．

師：哪些是我們已經學過的函數呢？

生1：第（2）個是一次函數，第（4）個是反比例函數．

師：那我們來看看余下的4個函數，它們有什么特點？

學生思考、交流、討論．

生3：我不同意，（5）與其它3個函數不一樣，右邊的式子不是二次整式，而是二次根式．

生4：它們都是二次整式．

師：非常好！你能類比一次函數的概念，嘗試給二次函數下定義嗎？

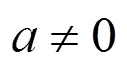
2.2 評析與思考

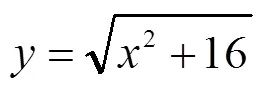
數學的嚴謹呈現為“冰冷的美麗”，但是數學的發現卻是“火熱的思考”[8]．二次函數概念不是憑空產生的，是源于函數知識本身發展的需要和必然，是基于情境問題解決之需要，這是概念形成的邏輯起點．通過問題驅動，蘊含于問題情境的新舊概念矛盾已經凸顯，引發了學生原有的認知沖突，從而誘使新概念的推出，為學生搭建了主動建構的問題支架，學生的思維自然而然地卷人其中，探求新函數的愿望油然而生，二次函數概念的形成亦水到渠成．

3 概念辨析 妙在釋疑

3.1 教學片斷呈現

本片段采用問答式，課堂氣氛活躍，學生發言踴躍，當學生做出判斷后，教師及時追問判斷理由．完成本例后，師生繼續對話．

師：通過這8個函數的辨析，你認為判斷二次函數的標準是什么？

生1：滿足兩個條件，首先，代數式部分應該整式；其次，自變量最高次是二次．

師：這8個函數中，（1）和（5）確定是二次函數，定義域是一切實數．把它放在實際問題中，如情境一、二中的二次函數，自變量的取值還是一切實數嗎？

師：為什么呢？

師：遇到實際問題時，自變量的取值范圍還要考慮實際問題是否有意義……

3.2 評析與思考

對于二次函數概念的理解，除了清楚概念的內涵，還必須明晰概念的外延．為此，教師根據學生的易錯、易漏、易混點，精選了8個函數，設置了兩個有價值的問題：為什么是二次函數？又為什么不是？以二次函數的正例和反例為載體，把新的基本概念從正反兩方面講[9]，在每一步“是”或“非”的問題上，小心質疑，讓學生“卷入”對概念的辨析、質疑、釋疑之中，達到豁然開朗的境地，逐步掌握判斷二次函數的標準，形成用概念作判斷的“基本規范”，推動學生對二次函數概念的內涵和外延的理解；然后進一步設問，豐富學生對自變量取值范圍的認知，為后續學習二次函數的相關知識提供有效保證．正如哲學家陸九淵所說：“學者有疑，小疑則小進，大疑則大進．疑者，覺悟之機也．一番覺悟，一番長進．”[2]

4 概念應用 卻要無疑

4.1 教學片斷呈現

例2 如圖2，在邊長為10的正方形中，是邊上一動點，以為邊長在形內作正方形，點在邊上，連接、．當在邊上運動時，探究圖中變量之間的函數關系．

圖2

圖3

師：（啟動幾何畫板，反復拖動點）請同學們觀察圖2，在點的運動過程中，圖形中哪些量發生變化？

生1：線段的長度，如線段、、、等．

師：還有其它量發生變化嗎？

生2：周長．

師：哪些周長？……還有嗎？

生2：△、△，還有正方形，它們的周長都在變．

生3：還有梯形的周長也在變，它們的面積也在隨著變化呢．

生4：角的大小也有發生變化……

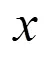
全班練習，學生先后主動板演．

師：生8，你能解釋一下為什么嗎？

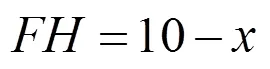
師：這些變化的量與x是一次函數關系，還有二次函數關系的嗎？

全班練習，適時交流討論，學生思維活躍，有答案后主動板演并講解理由．

生11：梯形的面積：

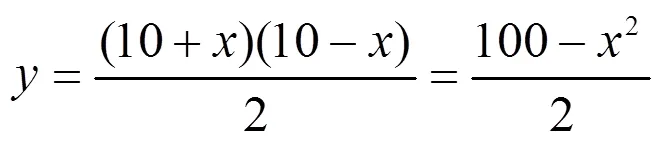
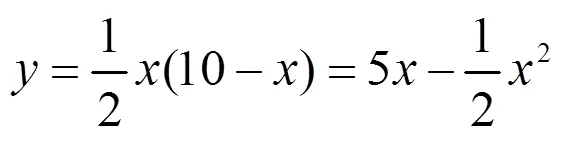
師：這些都是一次函數和二次函數，有沒有其它的函數關系呢？

……

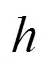
（1）分別求剛開始拋物與拋出4秒時，物體離地面的高度；

（2）拋出的物體經過幾秒鐘落到地面上？

教師活動：請生念題．電腦模擬上拋運動．（1）中剛開始拋物是什么時候？

師：（2）中什么叫落到地面上？

師總結：數學是學習物理和化學的工具……

4.2 評析與思考

例2的設置，充分展現了執教者的創新精神和數學素養，也是本課的最大創新和特色所在．該例問題開放，先任意找兩個變量，再建立函數關系，其結果可能是一次函數、二次函數，或其它函數．借助幾何畫板的動畫功能，啟動學生的幾何直覺思維，教師適時提出系列問題：“在點的運動過程中，圖形中哪些量發生變化?”“哪些變量與是一次函數關系?”“……還有二次函數關系嗎?”這系列問題以“理解性提問”和“評價性提問”為主[10]，都富有挑戰性，提問的受眾覆蓋面廣，為全體學生營建了平等和諧的思維場景，疑問不斷提出，又不斷被解決，學生的探究欲望被不斷激發，在激疑、生疑、釋疑的良性循環中，學生的思維自然發展，對二次函數的概念和與其它函數異同的理解有質的飛躍．然而，問題的解決又是獲得真知灼見的開始．當學生沉浸在“無疑”的喜悅中時，教師適切提出“這些都是一次函數和二次函數，有沒有其它的函數關系呢?”引發學生新的思考，激起新的思維波瀾，學生始終處于上下求索的憤悱狀態，有助于學生形成不斷質疑、釋疑的學習習慣，凸顯了數學的理性精神．正如張詩亞先生所說：“一惑剛去，一惑又來，如此循環往復、層層深入，促使學習者思維的發展與知識的增進．”[11]《學記》有說：“善問者如攻堅木，其先易難，后其節目．”講的也是這個道理．

在鞏固練習環節，教師基于數學知識內部蘊含的邏輯關系設置問題：當=0時，即是知自變量的值求函數值；當=0時，即知函數值求自變量的值；于物理問題中理解二次函數和一元二次方程的聯系，凸顯數學的工具性和應用性，也為跨學科發展學生問題意識提供例證．

5 概念延伸 須教有疑

5.1 教學片斷呈現

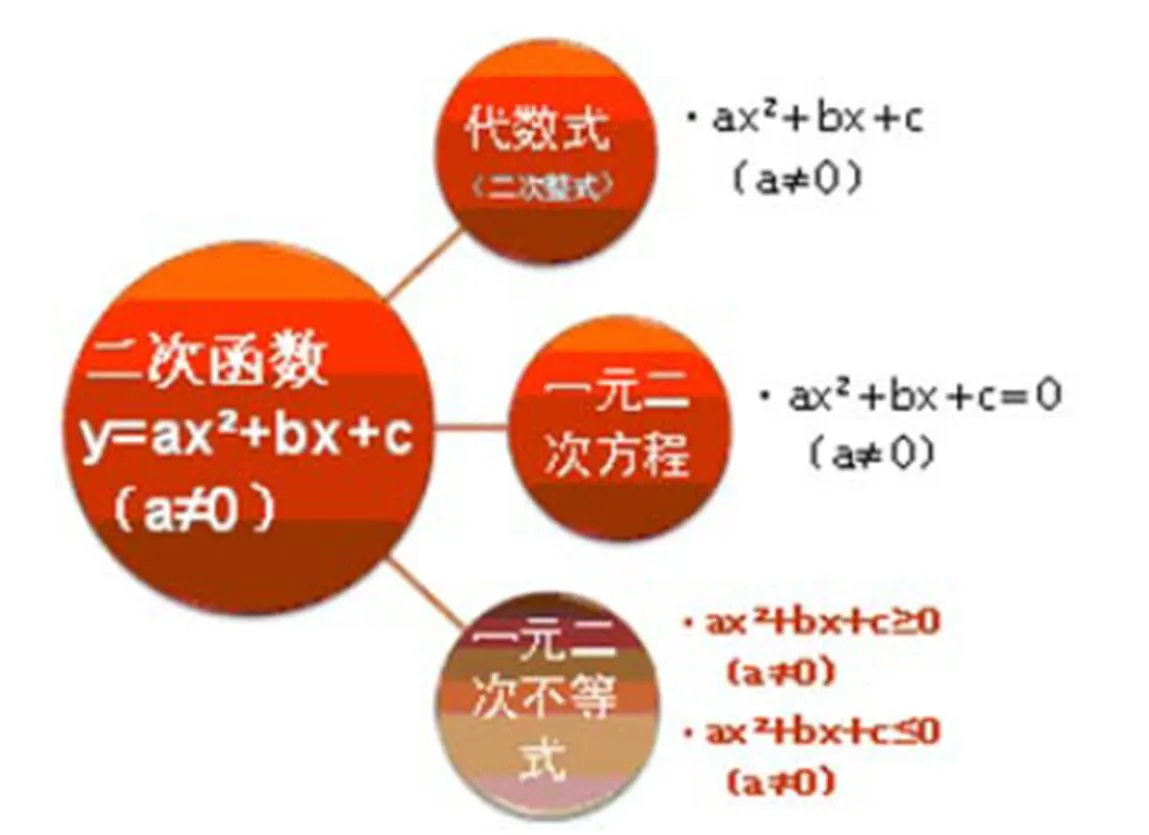
圖4

5.2 評析與思考

數學是充滿著聯系的，不要教孤立的片段，應該教連貫的材料[12]．因此，數學概念教學應幫助學生建立與相關概念的聯結，使當前概念與上位概念、下位概念結構化、網絡化、立體化，實現新舊概念的無縫對接．二次函數與已學函數，與二次整式、一元二次方程、一元二次不等式，彼此間存在著統一的數學關聯，通過課堂導學和小結，既能讓學生鏈接舊知，展望未來學習的相關內容，為學生建構與二次函數相關的數學知識系統提供了“機會和可能”，又給予了學生必要的數學學習方法指導，恰到好處地發揮數學的教育性，讓學生適時沐浴數學精神、思想與方法，獲得理性的數學思維的教育[13]．讓其帶著對“已知”的收獲與喜悅、對“未知”的好奇與疑問離開課堂，使學生產生“心求通而未得，口欲言而未能”的憤悱之感，進而達到課內向課外延伸之目的，這正可謂“言有盡而意無窮．”這就是數學的內在力量之所在！

總之，學生數學學習的過程是一個持續的“無疑—有疑—無疑”的動態循環和提高超越過程．在這個過程中，教師循“在無疑中發現問題——在生疑中提出問題——在質疑中分析問題——在釋疑中解決問題——在無疑中發現新的問題”的程式展開教學，其作用是“教有疑”與“教無疑”：當學生“無疑”時，教師要“須教有疑”，制造“山重水復”的窘境；當學生“有疑”時，教師則要“教而無疑”，不斷開創“柳暗花明”的勝景，這便是關于“有疑”與“無疑”的辨證處理要訣，也是“教有疑”和“教無疑”的理想境界．

在具體的教學實踐中，教師一方面要在學生的“思維生惑點”[14]設問，注重設問的有效性，從能力與方法上設問，從易錯易混角度上設問，從成長點和提高點設問，從開發潛能點上設問[13]．另一方面，教師要從整體規劃提問；有效運用元認知提示語；及時分析統整學生的回答；恰當創設疑境，引導學生提出有意義的問題等方面優化課堂設計，培養學生提出問題的能力[15~19]．當然，“疑”有深淺，“問”有大小，教師能否有效地提問和引發學生有效的疑問，源于教師的教學觀和學生觀，源于教師對課標和教材的理解，源于教師自身的問題意識，源于教師對數學教育的情懷．這也是未來數學教師著力之所在．期待數學課堂在踐行中豐腴，在豐腴中實現增值！

[1] 胡小松，朱德全．論數學教學設計的邏輯起點[J]．數學教育學報，2000，9（3）：33-36．

[2] 孫培青．教育名言錄[M]．上海：上海教育出版社，1984．

[3] 黃曉學，李艷利．論數學教學設計的創意生成點[J]．數學教育學報，2010，19（6）：9-12．

[4] 趙齊猛．數學課堂教學的邏輯結構[J]．中學數學教學參考：中旬，2013，（1-2）：34-38

[5] 李祎，曹益華．概念的本質與定義方式探究[J]．數學教育學報，2013，22（6）：5-8．

[6] 趙思林，朱德全．試論數學直覺思維的培養策略[J]．數學教育學報，2010，19（2）：23-26．

[7] 趙生初，許正川，盧秀敏．圖形變換與中國初中幾何課程的自然融合[J]．數學教育學報，2012，21（4）：95-99．

[8] 張奠宙，張蔭南．新概念：用問題驅動的數學教學[J]．高等數學研究，2004，（5）：10．

[9] 匡繼昌．如何理解和掌握數學概念的教學實踐與研究[J]．數學教育學報，2013，22（6）：74-78．

[10] 葉立軍，胡琴竹，斯海霞．錄像分析背景下的代數課堂教學提問研究[J]．數學教育學報，2010，19（3）：32-34．

[11] 張詩亞．教學中的以“惑”為誘[C]．南京：南京師范大學出版社，2010．

[12] 弗賴登塔爾．作為教育任務的數學[M]．陳昌平譯．上海：上海教育出版社，1999．

[13] 王光明．高效數學教學行為的特征[J]．數學教育學報，2011，20（1）：35-38．

[14] 黃曉學．論思維生惑點與數學教學[J]．數學教育學報，2007，16（2）：16-19．

[15] 溫建紅．論數學課堂預設提問的策略[J]．數學教育學報，2011，20（3）：4-6．

[16] 王光明，宋金錦，佘文娟，等．建立中學數學英才教育的數學課程系統——2014年中學英才教育數學課程研討會議綜述[J]．課程·教材·教法，2014，（5）：122-125．

[17] 李鵬，傅贏芳．論數學課堂提問的誤區與對策[J]．數學教育學報，2013，22（4）：97-100．

[18] 曹一鳴．數學教學中的“生活化”與“數學化”[J]．中國教育學刊，2006，（2）：46-48．

[19] 溫建紅．數學課堂有效提問的內涵及特征[J]．數學教育學報，2011，20（6）：11-15．

Discovering and Solving Problem——The Teaching Observation of Excellent Classroom Model: The Conception of Quadratic Function

TANG Fen1, ZHU De-quan2

(1. Yongchuan Middle School, Chongqing 402160, China; 2. Faculty of Education, Southwest University, Chongqing 400715, China)

The process of math study is the process of the circulation and transcendence of problem-discovering and problem solving .What teachers should do is to teach students how to pose question and then solve it; the aim of teaching is leading students into question which are ignored and solving the problem asked by them. Teaching students how to pose question and then solve it not only the dialectical treatment, but also the ideal state.

problem discovering; problem solving; question; conception; quadratic function

2014–07–21

中國基礎教育質量監測協同創新中心項目——數學素養體系構成與質量監測研究（ZJXT201402）

唐芬（1973—），女，重慶永川人，中學高級教師，主要從事中學數學教育教學研究．

G421

A

1004–9894（2014）06–0068–05

[責任編校：周學智]