第七屆“數學教育中的歷史與認識論歐洲暑期大學”綜述

朱 琳

?

第七屆“數學教育中的歷史與認識論歐洲暑期大學”綜述

朱 琳1，2

（1．華東師范大學 數學系，上海 200241；2．上海交通大學 數學系，上海 200240）

1 ESU7情況介紹

第七屆“數學教育中的歷史與認識論歐洲暑期大學”（European Summer University on the History and Episte- mology in Mathematics Education，簡稱ESU-7）于2014年7月13—18日在丹麥奧胡斯大學哥本哈根Emdrup校區召開．國際HPM組織前主席、法國南特大學的Evelyne Barbin，丹麥哥本哈根大學的Tinne Hoff Kjeldsen和丹麥奧古斯大學的Uffe Thomas Jankvist組織了本次大會．

1.1 ESU溯源

早在20世紀80年代初，法國數學教育學會發起并舉辦了“數學教育中的歷史與認識論暑期大學”．之后，歐洲范圍內成立了ESU組織，并于1993年在法國的蒙彼利埃（Montpellier）舉辦了第一屆“數學教育中的歷史與認識論歐洲暑期大學”．自此之后，ESU大會每隔3年舉辦一次，分別是1996年在葡萄牙的Braga，1999年在比利時的Louvain-la-Neuve和Leuven，2004年在瑞典的Uppsala，2007年在捷克的Prague，以及2010年在奧地利的Vienna．從2010年起，ESU改為每4年舉辦一次，和ICME的HPM衛星會議一起成為國際HPM組織委員會每兩年一次的HPM國際會議．

1.2 ESU的目標與宗旨

ESU的面向對象包括：對于數學史如何融入數學教學感興趣的中小學教師和大學師生，以及對于數學、數學史和認識論之間有所研究的數學史家和數學家．主要目標在于從歷史、認識論和文化的視角研究數學教學，尤其是課堂實踐；為數學教師、教育工作者和研究人員搭建一個分享教學思想和HPM課堂教學經驗的平臺；增進全世界數學教師和HPM研究者之間的合作．ESU關注的基于歷史與認識論的數學教育的重點在于：以自然發生的方式來揭示數學，將促進學生對具體數學知識的理解，并幫助他們理解數學的本質以及提升數學學習的效果、激發學生對于數學學習的興趣．

1.3 ESU7的主題

ESU-7主要聚焦在數學史和認識論研究指導下的課堂實踐教學，也關注有教學意義的理論觀點和歷史分析，包括7項研究主題：（1）在數學教育中融入數學史的理論和（或）概念框架；（2）從認知和情感視角觀察到的課堂實踐，以及對于課程和教材等教學材料的研究；（3）課堂上使用的原始材料以及實際的教學效果；（4）在數學和科學的教學中，以歷史和認識論為工具的跨學科方法；（5）文化與數學；（6）數學教育的歷史；（7）北歐國家的數學史研究．

2 ESU7會議內容

本屆會議參會代表包括來自法國、德國、英國、丹麥、意大利、美國、巴西、希臘、中國等地的數學史與數學教育專家，以及中小學教師和研究生等共計139人．會議共設大會報告6場，專題討論2場，2小時工作坊23場，3小時工作坊16場，以及口頭報告38場，簡短口頭報告和海報展示8場．

2.1 大會報告

ESU-7共安排了6場1小時大會報告，分屬7個主題．

意大利熱那亞大學的Adriano Demattè作了題為“課堂中的歷史：教育的時機和開放的問題”的報告，該報告屬于主題2和3．Demattè教授從理論角度批判性地分析了如下問題：詮釋學和發生教學法能共存嗎？數學史能提高哪種跨學科的能力？哪一類學生能從中受益？相反學生又會從中產生哪些額外的困難？哪些會受到課程的限制？并介紹了他在課堂中的一些教學案例．他同時強調，由于日常課堂教學活動的復雜性，不能簡單從幾個案例中得到問題的最終答案．

法國南特大學的Evelyne Barbin在其報告中梳理了自弗賴登塔爾1983年國際數學家大會的報告[1]之后30年來有關HPM研究的文獻，重點介紹在對歷史的理解和對歷史和教育之間關系的理解下，所構建的數學史融入數學教育的理論框架．該報告屬于主題1．她還在后續的工作坊中詳細介紹文獻綜述中所引用的原始文獻和歷史材料．

分屬主題4的大會報告是法國巴黎七大Cécile de Hosson的“通過使用早期希臘和中國宇宙學中的歷史材料提升跨學科教學”．傳統教學中，數學和科學這兩個學科是相互分離的．通過古代希臘和中國宇宙學中的兩個歷史片段，融入數學和科學這種跨學科的教學，將在一定程度上改變學生對于科學本質的認識．Hosson教授在報告中介紹了古代中國的《周髀算經》、張衡的渾天儀、趙爽對“日高術”的證明等歷史材料．遺憾的是，她介紹重差術時所描述的相似三角形原理，與趙爽的面積割補原理是有出入的．

來自冰島大學的Kristin Bjarnadottir作了題為“歷法和貨幣——融入文化、自然、社會和語言”的大會報告，屬于主題5．通過介紹不同社會中所使用的歷法和貨幣，讓學生認識到這是所處的文化和語言環境的不同反映，由此促進對不同文化環境中的相關數學主題的理解．

巴西里約熱內盧聯邦大學GertSchubring的報告“數學教育史的一些新方法和結果”屬于主題6．他介紹，數學教育史的第一篇博士論文誕生于20世紀初，其后的相關研究都是數學教育的國別史．自第一份國際期刊《國際數學教育史雜志》（IJHME）于2006年創刊后，研究的重點轉變到關于數學教育史的國際比較研究．Schubring教授介紹了自己的一些比較研究成果．

分屬主題7的是南丹麥大學Bjarne Toft的“圖論的出現：彼得森（Julius Petersen，1839—1910）和西爾維斯特（James Joseph Sylvester，1814—1897）”，他以幽默的語言、生動的講述，為大家介紹了丹麥數學家彼得森在正則圖理論誕生過程中發生的歷史故事．

2.2 專題討論

大會設有兩場專題討論，每場由5名學者分別闡述觀點，互相辯論，并與現場發言者進行討論和互動，引發與會者極大的關注和思考．第一場專題討論的主題為“數學教育中信息技術的歷史和哲學方法”，討論包括如下3個問題：（1）教學活動中計算機技術的使用是如何改變數學學習過程的？這種改變的程度如何？數學是什么？數學是如何理解和學習的？（2）數學教育中要持續使用計算機技術嗎？（3）計算機技術在做數學和學數學中有哪些不同？專題討論中提到了影響數學教育的不同領域，包括學科領域、專業領域、學術領域以及學生的日常生活領域，并特別強調：不同的理論要求不同領域的實證研究問題與教育教學建議．第二場專題討論的主題為“數學史融入數學教育的課堂評價”，由來自英國、美國、德國、法國的5名學者探討了在數學史材料融入課堂教學中，如何建立定性和定量的評價模式，來評估課堂教學活動的效果．

2.3 工作坊

歷時5天的大會共開設了39場工作坊，在相同時間里同時進行多場工作坊．由組織者準備有關歷史、認識論、教學法以及教學的原始材料，分發給參與者進行閱讀和思考，并展開充分的分析和討論．其中，2小時工作坊討論的主要是課堂教學材料，3小時工作坊討論的主要是關于歷史和認識論材料．各工作坊的主題分布如圖1所示．

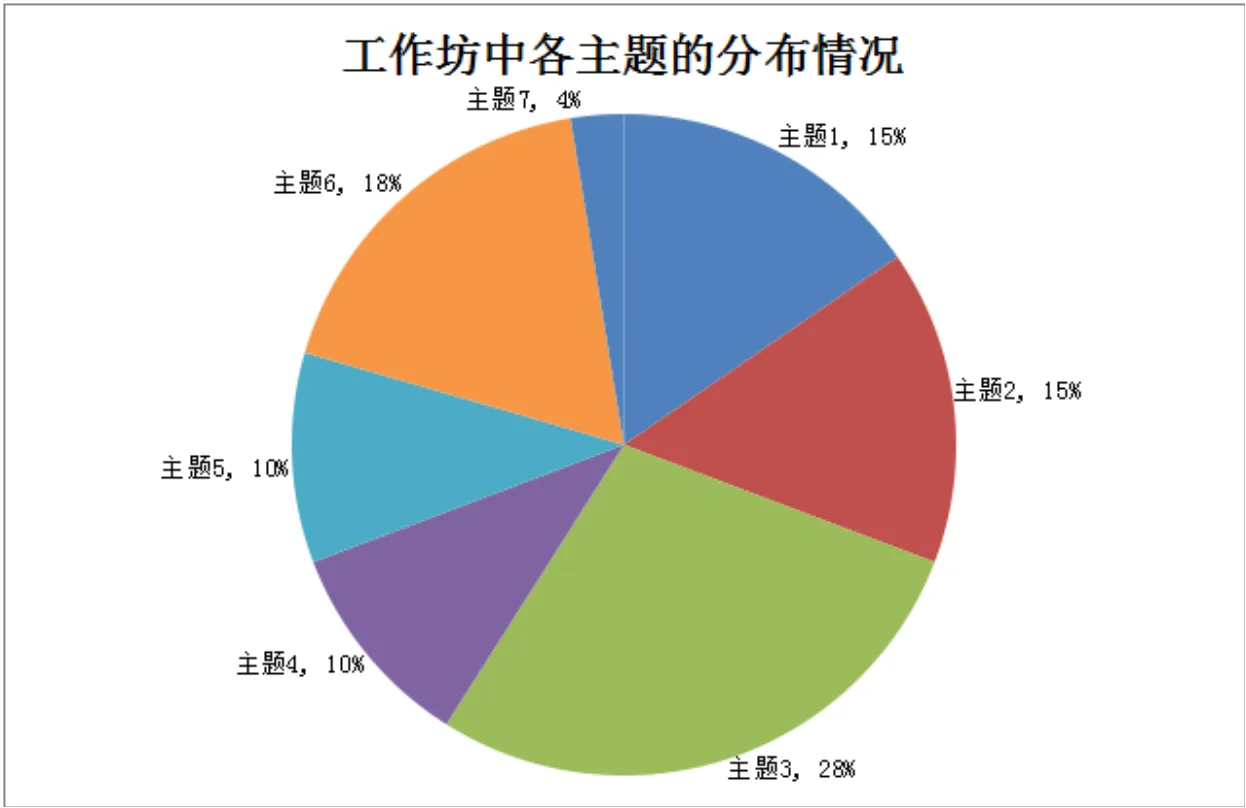
圖1 工作坊的大會主題分布

工作坊以靈活多樣的形式，展示了報告人在相關主題的實踐和研究，并由報告人帶領參與者一起閱讀原始文獻、研究文獻、課堂講義等，針對相關主題進行討論和思考．表1給出了各工作坊主題的內容．

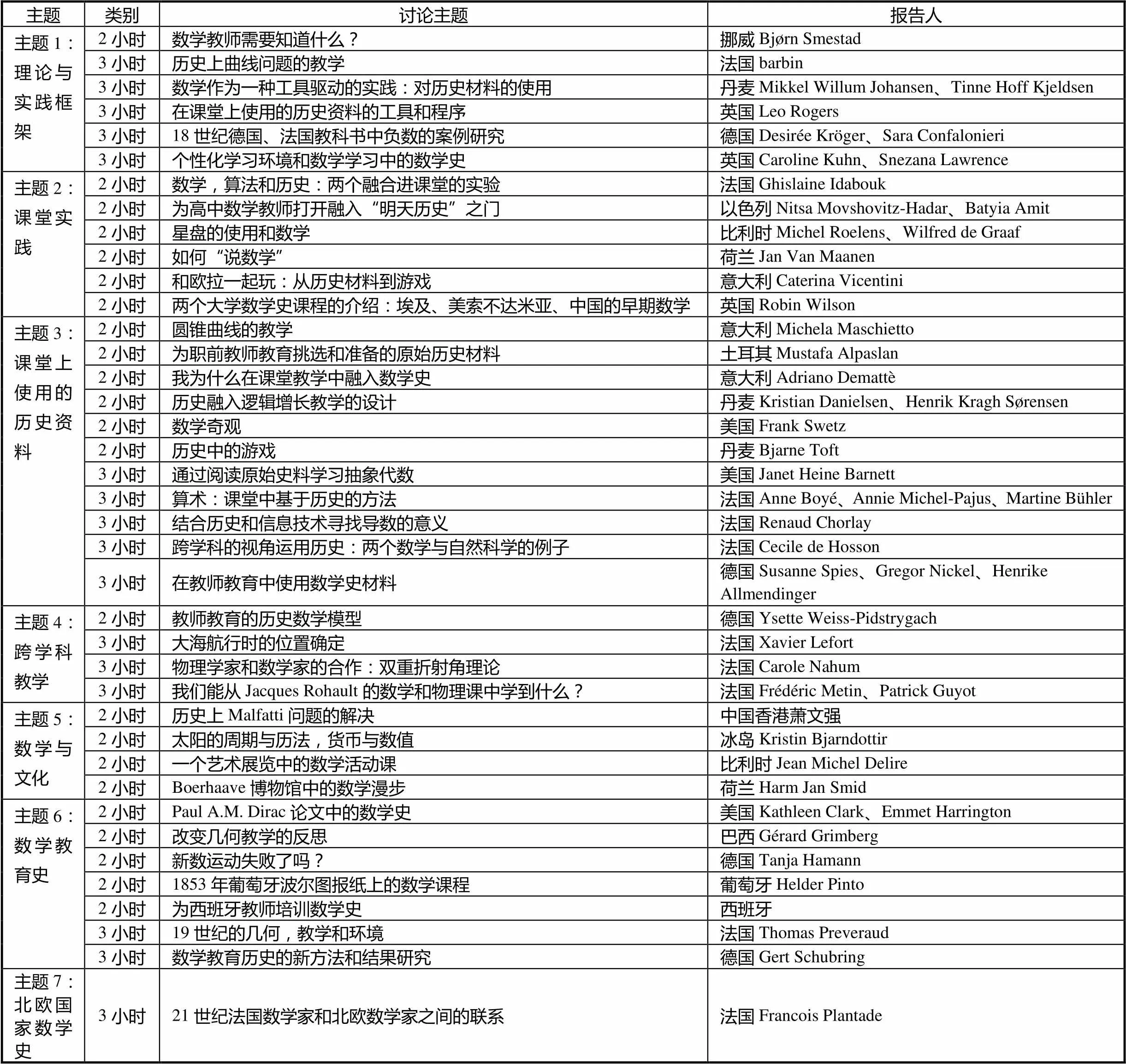
表1 工作坊統計

2.4 口頭報告和海報展示

38場口頭報告也是在不同的時間段中分別同時進行．表2給出了各主題的分布情況．

表2 口頭報告主題分布

注：ESU大會將主題2定為課堂實踐觀察以及課程和教材等教學材料的研究，將主題3定為課堂上使用的原始材料以及實際的教學效果研究，這兩個主題相互交叉很難嚴格區分，因此在大會報告和口頭報告環節，相關主題都歸入主題2&主題3．

與此可見，對于在數學教育中融入數學史的理論和概念框架的研究，共計18場，占了口頭報告的主要部分．其中，德國學者Hans Niels Jahnke闡述了托普利茲發生教學法的意義和內容；華東師范大學汪曉勤教授綜述了中國大陸HPM研究領域的進展，并將數學史融入數學教學的方式分成附加式、復制式、順應式和重構式；巴西學者Aline Bernardes 和Tatiana Roque基于Sfard“思考即交流”以及Epple認識對象和認識技術的概念理論進行分析，設計將矩陣的歷史融入數學課堂的教學活動；華東師范大學的王科介紹了HPM領域的設計研究方法：包括調研與分析、開發與設計、執行與操作、分析與評估、應用與推廣5個階段，并形成了教師知識領域、數學教育者知識領域和數學史專家知識領域的HPM三棱錐模型；墨西哥Gabriela Buendía Abalos從“為何”角度，闡述認識論是確定教學方式的重要基礎，并探討了發展數學史融入教學理論的必要性；法國的Thomas Hausberger則介紹了基于在Montpellier大學實施的教學實驗所得到的關于歷史和認識論的理論及實踐框架．

主題2及主題3的口頭報告涉及實際的課堂教學案例以及課堂教學材料，內容包括對數概念教學、統計學、圓的大小關系比較、幾何軟件解決數學問題、圓的面積教學、橢圓教學等方面．

15分鐘的簡短口頭報告和海報展示共計8場．其中1場介紹“數學，教育和戰爭”，屬于主題5；其余均屬于主題2和主題3，包括意大利Miglena Asenova概率案例的實證研究，意大利Michela Maschietto的報告“帕斯卡：從歷史到課堂”，墨西哥Alejandro Rosas-Mendoza對于殘疾學生這一特殊教育的介紹，墨西哥Leticia del Rocío Pardo-Mota對于中國古代數學中級數和序列的研究，以及華東師范大學朱琳介紹的數學史融入導數幾何意義教學的課堂案例和美國Laurence Kirby展示的“從古代數學到現代數學”視頻．

3 ESU7會議內容的特點

3.1 重視教育取向的數學史原始資料的挖掘

數學是人類幾千年發展歷史中智慧的結晶．漫漫歷史長河中，數學史的資源取之不盡用之不竭．HPM的研究不是為歷史而研究歷史，而是為教育而研究歷史，是教育取向的數學史研究[2]，需要挖掘尋找適合課堂教學的數學史，并針對原始歷史素材和資料進行“再創造”．Frank Swetz介紹了古希臘、古羅馬、古代中國歷史中豐富的數學史資源；Michel Roelens利用歐洲戰爭中使用的星盤教學生計算白天的長度、決定當地時間等，激發學生對數學和自然科學的興趣；Caterina Vicentini開創了“數學游戲角”，利用歐拉的代數算法發明了關于算術級數的游戲；Kathleen Clark研究了諾貝爾物理學獎得主保羅·狄拉克（Paul A. M. Dirac，1902—1984）解決多項式方程的方法，并與歷史上其它的方法進行比較；蕭文強研究了著名的Malfatti問題：給定三角形中3個內接圓形的幾何問題；Tinne Hoff Kjeldsen介紹了卡爾達諾和沃利斯發明復數的兩種不同方法；Klaus Volkert介紹了18世紀的平行線問題，等等．尤其值得關注的是，本次ESU7中由西方學者介紹的古代中國數學史專題涉及1個大會報告、3場工作坊和5個口頭報告（含簡短口頭報告），內容包括《九章算術》、《周髀算經》、《圓容較義》等古代中國數學名著以及割圓術、重差術、中國剩余定理等數學思想和方法以及幻方、數獨等古老中國的數學游戲，與此可見西方學者對東方數學史的重視與研究．

3.2 關注實際的課堂教學和實踐

HPM研究的目的是“為教育而歷史”，要把數學史融入數學教學，不僅著眼于理論研究，更重要的是實踐開發[3]．本次大會工作坊和口頭報告環節，涉及實際課堂教學的比例分別為43%和21%，可見比重之重．其中，Michela Maschietto用阿波利尼斯的錐形槽模型和旦德林球模型引入圓錐曲線教學；JanetHeineBarnett指導學生通過閱讀拉格朗日、柯西、凱萊關于群論的原始講義，以歷史發生的順序講解抽象代數知識；RenaudChorlay基于《幾何原本》和古巴比倫求近似平方根的方法，利用動態幾何軟件設計3種不同的學習導數的課堂活動；GhislaineIdabouk利用歷史上海倫求根的近似值的方法指導教學，并分析了歷史材料使用和歷史視角教學的相關性．

3.3 強調數學史在教師教育中的作用

教師是HPM教學和研究的主體，教師的HPM能力和素養是數學史融入數學教學的根本和保證．教師教育關注的研究主要分為職前教師教育和在職教師培訓．本次大會中，與教師教育的HPM研究相關的工作坊有7個，包括以色列在職教師教育中介紹“明天的歷史”，土耳其在職前教師教育中指導教師挑選和準備原始歷史資料，丹麥在職前教師教育中設計歷史融入邏輯增長的教學案例，以及德國和西班牙的教師教育項目介紹．口頭報告也有3個主題與教師教育相關，包括“教師反思中傳統與非傳統觀點的交叉問題”、“用數學教育中的社會文化方法來調查職前中學教師的數學史能力”以及“職前教師對數學的理解”．

3.4 中國大陸HPM研究首次走進ESU

值得一提的是，共有7位中國大陸HPM研究者參加了ESU-7．其中6人各作了30分鐘的口頭報告，1人作了15分鐘的簡短口頭報告和海報展示，主題包括汪曉勤：“中國大陸的HPM研究”、王科：“設計研究——HPM研究領域的新范式”、林佳樂：“HPM的理論框架”這些理論探討，還有田方琳：“數學史融入對數概念教學”、洪燕君：“HPM視角下圓的面積教學”、鄒佳晨：“發生教學法教橢圓”以及朱琳：“發生教學法教導數”的實踐教學案例研究．據香港大學的蕭文強教授回憶，在HPM領域的國際會議中，大陸學者最早是華東師范大學張奠宙教授1988年在法國馬賽Luminy鎮參加的由ICME發起，HPM主辦的“數學史在數學教育中的作用”國際研討會．此后陸續有郭書春、曲安京等大陸學者參與ICME的HPM衛星會議．但在此之前，華人學者中只有蕭文強教授曾經參加ESU會議．作為大陸學者第一次參加ESU這一使用英語為通用語言的國際性學術會議，ESU-7標志著中國大陸HPM研究首次以團隊展示形式走向了世界．

4 若干啟示

4.1 HPM理論框架的構建

HPM組織自從1972年成立至今，數學史與數學教育之間的關系從為何到如何的討論已經逐漸走向成熟．克萊因、卡約里等數學家、數學教育家都曾高度評價數學史在數學教育中的價值和作用，數學史在數學教育中的意義得到更多的關注、重視和認同．海克爾的“個體發展重演種族發展”、弗賴登塔爾的再創造理論、建構主義、發生教學法，都從各方面提供了HPM研究的方法．而今的HPM研究，又越來越多地與信息技術、數學教育心理學、認知理論等相結合．HPM的課堂需要有合適的課堂評價模型以評價教學效果和教育價值．這些都需要研究者在理論研究的基礎上，結合實證研究的方法，進行深入地研究和思考，在前人工作基礎上構建理論和實踐領域的框架模型．

4.2 HPM教學案例的深入開發與實踐

哪些數學史材料能夠用于課堂教學？如何將數學史材料用于課堂教學？這些問題需要在課堂教學的實踐中進行進一步的研究和驗證．HPM研究者的任務，是要選擇合適的數學專題，挖掘原始的歷史資料和材料，對歷史資料進行重構與“再創造”，以開發出適合課堂實際教學的案例．歷史的寶藏博大精深，任一數學專題的教學，如導數、對數、負數的教學案例，都有豐富的史料可以利用，有不同方案的教學設計．HPM研究者與教師一起，對教學案例進行深入的開發和實踐，是HPM研究領域的重要工作．

4.3 HPM與教師教育的研究

數學史是數學教師用于數學教學的必備知識[4]，而職前教師和在職教師是實現HPM實踐教學的關鍵因素．通過設計和開發相應的職前和在職教師培訓項目的課程，提升數學教師的數學史素養，并提高他們運用數學史融入數學教學的能力，對教師專業能力的成長和HPM研究的深入開展，都是不可或缺的重要部分．

4.4 中國HPM研究者的工作任重道遠

中國大陸的HPM研究第一次走進ESU國際會議，從理論探討、研究方法探索到實踐案例開發設計，作了充分精彩的展示，引起了西方學者的進一步關注和東西方之間HPM領域的深入交流．大陸的HPM研究者還需要克服語言障礙，深入整理研究成果和案例，在國際HPM學術期刊上進行公開發表和宣傳，以更加積極的姿態活躍于國際HPM學術舞臺．同時要看到，由于中國古文、英文、法文等數學史文獻翻譯的問題，很遺憾出現了一些錯誤．需要大陸HPM學者乃至數學史研究者對古代中國數學史進行進一步的宣傳和校正，以更加準確地傳播古老東方的數學史成果和思想精髓．東西方的數學史與數學教育還需繼續深入地交融合作，反思對方的做法和經驗，建立適用的理論和實踐，以真正提高數學史融入數學教育的理論和實踐水平．

2014–08–12

G40-034

A

1004–9894（2014）06–0086–04

[責任編校：周學智]