基于Rao－Blackwellised粒子濾波的巖石聲發射信號去噪

凌同華，劉偉宏，朱 亮，吳聯迎

在巖石聲發射的信號處理中，信號去噪是最基礎、也是最關鍵的一項工作。目前，信號去噪處理的方法主要有兩種：頻域和時間－空間域分析方法。假設噪聲和期望信號成分在頻域范圍內相互不重疊，可以通過頻域方法濾除噪聲（如：高通濾波、帶通濾波及帶阻濾波等）。例如：白噪聲分布于整個頻域范圍內，傳統的頻域方法已經不能清除噪聲成分。相反，一種基于噪聲統計特性的狀態空間方法被用來去除噪聲成分。在時域上建立起來的常用濾波有：維納濾波、卡爾曼濾波［1－2］及擴展卡爾曼濾波等。維納濾波局限于處理線性平穩靜態過程，并具有很好的效果。卡爾曼濾波常被用于處理非靜態過程的信號。當需要確保濾波精度時，動態系統需滿足線性且噪聲服從高斯白噪聲分布。另外，擴展卡爾曼濾波已被用來處理非線性系統，但對預測狀態的估值問題仍需線性化處理，噪聲要求服從高斯分布。

近幾年，迅速發展起來的粒子濾波［3－5］（Particle Filter，簡稱為PF）是一種基于蒙特卡羅的非線性、非高斯系統狀態估計的濾波方法，完全突破了卡爾曼濾波理論框架，對系統的過程噪音和量測噪音不加任何限制。在PF基礎上，作者擬提出Rao－Blackwellised 粒 子 濾 波 （Rao－Blackwellised particle filter，簡稱為RBPF）來加強巖石聲發射信號采集質量。

1 粒子濾波

從動態系統中獲取信息和估計系統的狀態，建立一個精確的模型是至關重要的。大多數物理現象服從隨機分布，其狀態可以用有限維向量描述，并通過向量差分方程來模擬。建立PF系統模型，至少需要兩個方程：①狀態方程，用于描述系統狀態隨時間演變的過程；②觀測方程，用于將系統在某時刻的輸出和系統的狀態聯系起來。

式中：Xk，Yk分別為動態系統在k時刻的狀態向量和觀測向量；f 為狀態函數；h為觀測函數；Wk－1，Uk分別為狀態過程和觀測過程的噪聲。

粒子濾波算法流程如圖1所示，其詳細過程見文獻［3，4］。

圖1 PF算法流程Fig.1 Flow chart of PF algorithm

2 Rao－Blackwellised粒子濾波

2.1 RBPF方法

由于聲發射信號的采集頻率比較高（通常在兆赫茲以上），粒子濾波需要大量的樣本點來組建后驗概率分布，使計算效率下降。尤其在高維狀態空間和實時監控應用中，計算效率下降較明顯。為實現粒子濾波在實時聲發射監控中應用，采取具有降維作用的 RBPF［6－9］。

RBPF將標準狀態空間向量xk分解成兩個子空間，其中一部分x1k可以通過卡爾曼濾波進行分析解計算；而另一部分x2k可通過粒子濾波計算，并使其計算的復雜程度大大降低。RBPF的目的就是用較少的粒子獲取同樣的估計精度，從而降低計算量，實現其成本的節約與推廣應用。基于兩個子空間所構成的條件概率，并對其進行推演：

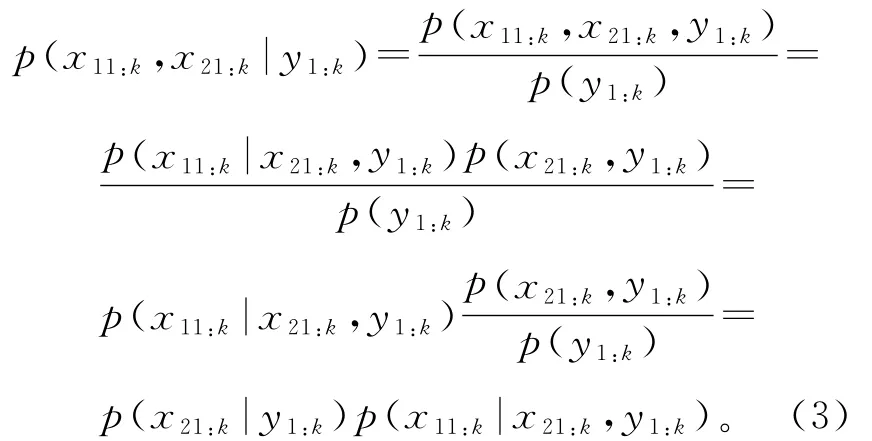
式中：p（x21：k｜y1：k）為x21：k的后驗概率密度函數。

如果p（x11：k｜x21：k，y1：k）服從條件線性高斯分布，則可通過卡爾曼濾波實現其最優估計。因此，由兩個子空間構成的后驗概率密度函數通過運用粒子濾波估計時，僅需考慮與x21：k相關的一部分。RBPF可以看成是卡爾曼濾波與粒子濾波的結合體，是一種加強的粒子濾波。

2.2 RBPF實時處理特征

RBPF是一種狀態空間時域的濾波技術，每次輸入一個新的數據算法立即更新。在更新過程中，RBPF不依賴于全部已輸入的信號序列，僅需考慮前一時刻的數據。因此，在采集過程處理信號時，對采集數據長度和采樣頻率沒有特殊要求，此外，RBPF在計算過程所需存儲數據的空間將大大降低，其運算速度獲得較大的提高。斷鉛試驗常被用來模擬聲發射源，斷鉛試驗中采集的聲發射信號如圖2所示。從圖2中可以看出，濾波效果不受采集數據長度的影響。RBPF進行信號去噪處理時不受將來采集數據的干擾，僅與當前時刻及前一時刻所處的狀態有關。傳統的濾波器不具有這一特征，在濾波過程中需要完整的數據鏈。由于RBPF有實時在線處理功能，并能處理高維的非線性非高斯系統，而備受研究者的關注。

圖2 RBPF實時處理信號濾波的特征Fig.2 The real－time processing feature of RBPF based signal filtering

3 RBPF在聲發射信號去噪中應用

3.1 狀態空間模型的建立

由于地震波信號與聲發射信號具有相似性，地震波模型可以成為合適的候選對象來代表結構中的聲發射事件。其模型為：

式中：A1（t－t0）為聲發射源波形的振幅；t0為波形到達時間；ω為主導角頻率（ω＝2πf）。

在處理地震數據中，類似的方法被其他學者采用，地震波的振幅可用隨機過程X1（t）表示，同時地震波用隨機過程Xw（t）表示，則該過程可以改寫為：

式中：δ（t）為相位角。

由于高斯－馬爾卡夫（Gauss－Markov）過程能用來模擬許多物理現象，其中也包括模擬地震波的振幅X1（t），其離散形式為：

假定狀態空間的噪聲部分也可用高斯－馬爾卡夫過程代替，其表達式為：

式中：aX2，bX2均為高斯－馬爾卡夫過程的參數；w2與w1相互獨立。

這些方程中涉及的參數可通過聲發射信號的噪聲部分確定。

利用模型式（6），（7），聲發射的狀態空間系統可以構造為：

此外，其量測方程構造為：

式中：ωk為第k時間步長的主頻率；vk為量測噪聲。

式（8），（9）可分別用簡化的矩陣形式表示為：

由于沒有固定的主導角頻率，通過運用頻率粒子集［ωik］Mi＝1，會比運用具體指定的頻率有更高的估計精度。在研究中，每一個粒子的動態函數和量測函數分別為：

從式（12），（13）可知，每一個粒子的狀態和量測函數均為線性。從另一個角度來說，本研究提出了用RBPF的方法來估計聲發射信號，即由標準卡爾曼濾波處理狀態更新，同時利用粒子濾波處理非線性的量測函數。

3.2 基于聲發射信號去噪的RBPF算法

完整RBPF算法的步驟為：

1）卡爾曼濾波初始化：X1（0）＝0，X2（0）＝Y0；誤差協方差在實驗過程中，發現：R選擇相對較大值時，能得到一個較滿意的結果；遞推過程收斂時，R的選取對濾波結果影響甚小。

2）狀態估計預測和誤差協方差預測：

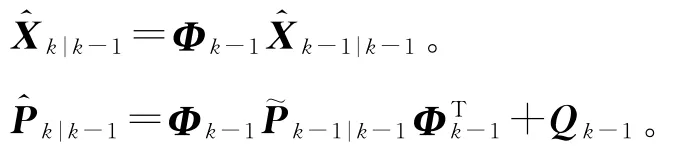
3）粒子更新：

①采樣ωik～p（ωk），zik＝sin（ωikkΔ），i＝1，2，…，M；

②計算外推量測估計和方差：

式中：Rk為量測函數中觀測噪聲的方差，即vk～（0，Rk）。

③計算預測密度：

④計算每個粒子的重要性權重：

⑥更新量測矩陣：G～k＝［1 z～k］。

8）設定k＝k＋1，回到步驟2）。

針對算法中出現的參數，需要說明：

Φk－1能夠根據狀態函數的先驗知識設定初值，Φk－1可分兩種情況考慮：①時變性，即隨時間需要更新或傳遞；②時不變性。在巖石沖擊聲發射實驗中，由于實驗環境相對較簡單，且RBPF用于聲發射信號去噪目前處于探索性階段，因此僅考慮時不變性，設定，其中：a1，a2均為高斯－馬爾卡夫過程中的參數，詳細的解釋可參考式（6），（7）。a1，a2合適的取值可以從信號的噪聲部分（沒有目標信號參與進行采集）和附有噪聲的信號序列中獲取。

Qk－1為狀態過程噪聲的協方差，其表達式為：

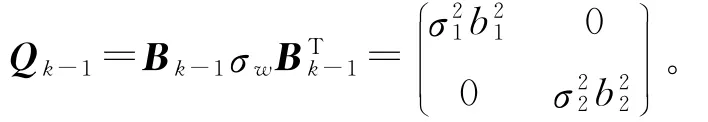
假定噪聲的方差為時不變隨機過程，那么，Qk－1為固定值Q。Q矩陣可通過信號的噪聲部分初始化，確定Q的步驟為：①采集沒有目標信號參與的噪聲信號，即采集周圍噪聲；②計算采集噪聲信號的自相關性；③利用模型σ2e－β｜τ｜對自相關數據進行擬合，其中：σ，β均通過回歸分析確定。

利用該方法可獲得σX2和βX2。在探討過程中，觀測噪聲的方差假定為相對較小的常數。

3.3 RBPF仿真實驗

為檢驗RBPF的濾波效果，借助于Matlab對其進行仿真模擬。首先需要構造一個不受噪聲污染的原始信號作為標準信號，便于與其加噪處理后進行濾波所得結果比較。為驗證RBPF處理噪聲信號的效果，需對原始信號（如圖3（a）所示）加入高斯密度分布的噪聲，其附加噪聲的方差為0.2，附加噪聲的信號如圖3（b）所示。對加噪信號運用RBPF進行濾波處理，處理后的信號如圖3（c）所示。

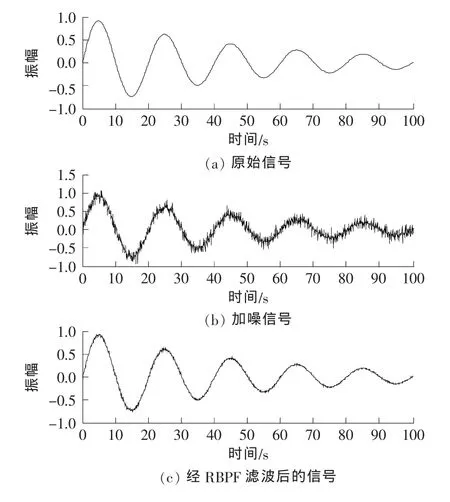
圖3 仿真結果Fig.3 Simulation results

從圖3中可以看出，RBPF在信號去噪處理中能獲得較好的濾波效果。

3.4 RBPF在聲發射信號去噪中應用

試驗數據來源：利用SHPB系統對兩組石灰巖進行沖擊荷載作用下聲發射試驗，具體試驗裝置如圖4所示。采集兩組聲發射數據X11和X21，在采集過程中有噪聲干擾，利用本研究提出的RBPF處理采集的聲發射數據，對應的去噪信號分別為X21和X22，經RBPF后的結果如圖5所示。

圖4 SHPB測試系統Fig.4 SHPB testing systems

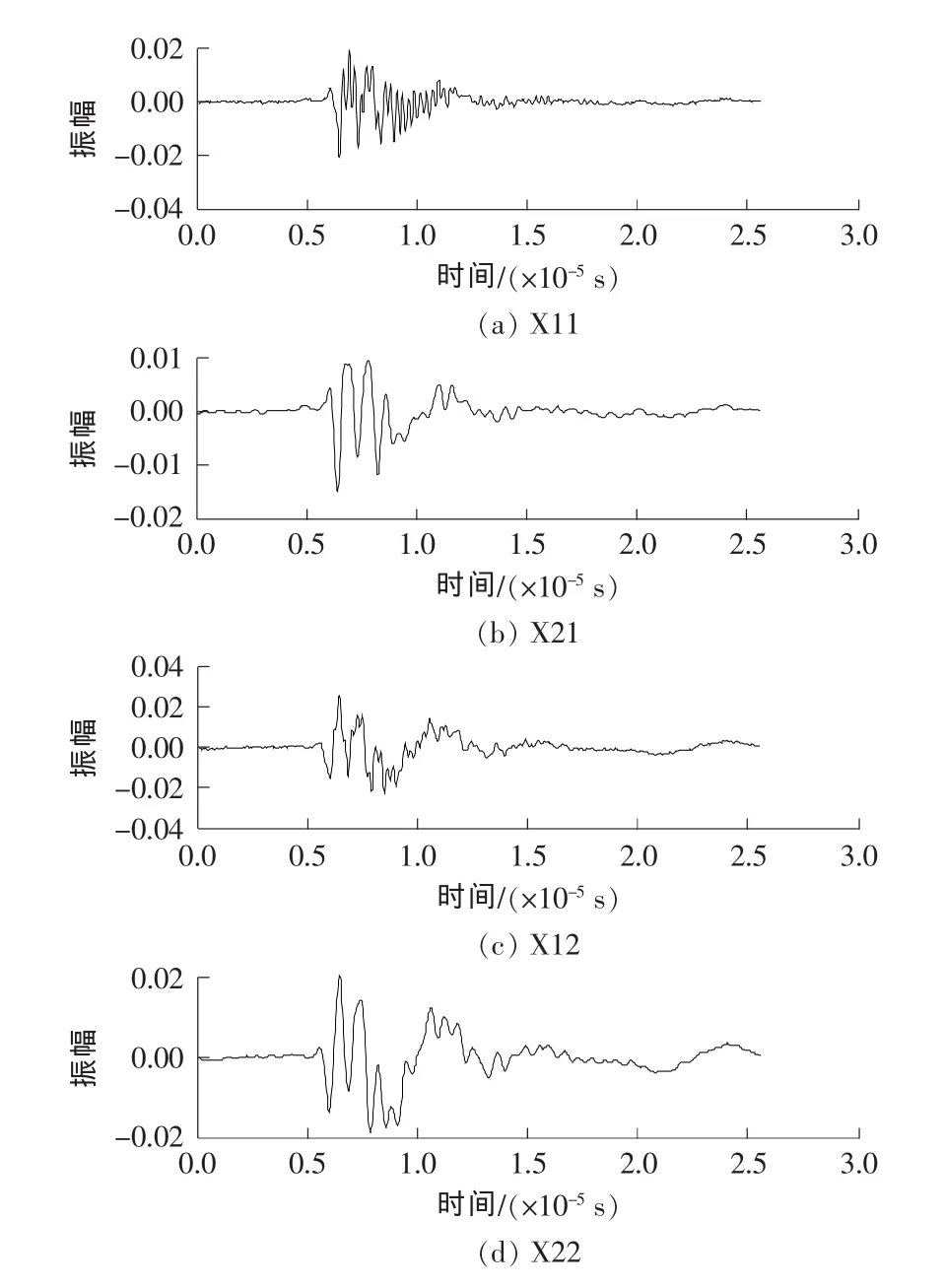
圖5 X11和X21為原始信號，X12和X22為其對應的去噪信號Fig.5 X11and X21as original signals，X12and X22as corresponding denoising signals

在處理兩組聲發射數據時，粒子總數取200，噪聲按高斯－馬爾卡夫過程模擬，計算時間常數Tc＝4.5×10－4ms，方差σ＝6.7×10－3v2。聲發射源的采樣頻率40MHz，并遵循假設：開始波形的振幅為零，X1（1）＝0；第一個測量值y1設定為噪聲，即X2（1）＝y1。

為進一步分析聲發射數據并檢驗RBPF的效果，利用FFT求出圖5中各信號的頻譜圖，如圖6所示。從圖6中可以看出，X11最大振幅所對應的頻率分別為0.15，1和3MHz，而X21最大振幅所對應的頻率分別為0.15和1MHz。X21在0.15和1MHz對應的幅值分別高于X11所對應的點，而在3MHz時，兩者相差不大，甚至低于X11的，在3MHz出現的現象由噪聲所致。通過RBPF對原始信號進行去噪，發現兩者在3MHz的幅值都趨于零。可見，RBPF在處理聲發射信號中具有很大的潛力。

圖6 圖5中對應信號的頻譜Fig.6 Spectrogram of the corresponding signal in Fig.5

4 結論

本研究提出了一種時空濾波方法RBPF，并對聲發射信號進行去噪處理。通過合理選擇模型參數，由實驗結果驗證了RBPF能夠加強聲發射信號的信噪比，并保留其主要頻率成分。實驗中還發現，沖擊荷載作用下石灰巖最大振幅所對應的頻率為0.15和1MHz，這對爆破與機械震動作用下的聲發射監控有著重要的參考價值。

值得注意的是：論文研究模型最初來源于其他學者用來處理地震數據。由于考慮到聲發射與地震波具有一些共通性，通過修正其模型參數，延伸到RBPF處理聲發射信號中，并取得了不錯的效果。然而，對聲發射信號最優模型的建立和過程，噪聲特征仍需作進一步的研究。

（

）：

［1］ Niri E D，Farhidzadeh A，Salamone S.Nonlinear Kalman filtering for acoustic emission source localization in anisotropic panels［J］.Ultrasonics，2014，54：486－501.

［2］ Baziw E，Jones I W.Application of Kalman filtering techniques for microseismic event detection［J］.Pure and Applied Geophysic，2002，159：449－471.

［3］ Zhang W M，Du G，Zhong S，et al.Study of nonlinear filter methods：Particle filter［J］.Journal of Systems Engineering and Electronics，2006，17（1）：1－5.

［4］ Petar M D，Jayesh H K，Zhang J Q，et al.Particle filtering［J］.IEEE Signal Processing Magazine，2003，20（5）：19－38.

［5］ Zhou C J，Zhang Y F.Particle filter based noise removal method for acoustic emission signals［J］.Mechanical Systems and Signal Processing，2012，28：63－77.

［6］ Menéndez R M，Freitas N，Poole D.Dynamic modelling and control of industrial processes with particle filtering algorithms［J］.Computer Aided Chemical Engineering，2004，18：721－726.

［7］ Freitas N.Rao－blackwellised particle filtering for fault diagnosis［J］.IEEE Aerospace Conference Proceedings，2002，4：1767－1772.

［8］ Mustière F，Bolic＇M，Bouchard M.Rao－Blackwellised particle filters：Examples of application［A］.IEEE CCECE／CCGEI［C］.Ottawa，Canada：［s.n.］，2006：1196－1200.

［9］ 潘宏俠，門吉芳.粒子濾波在軸承故障振動信號降噪中的應用［J］.振動、測試與診斷，2011，31（3）：354－356.（Pan Hong－xia，Men Ji－fang.Bearing fault vibration signal noise reduction based on particle filtering［J］.Journal of Vibration，Measurement ＆ Diagnosis，2011，31（3）：354－356.（in Chinese））