注重培養學生數學思維的三點做法

邵祖祥

摘要：本文從抓本質，優化教學設計；抓聯系，貫通知識整體；抓關鍵，關注教學細節三個方面探討了提升小學生數學思維能力的有效方法。

關鍵詞：小學數學；思維培養；方法

中圖分類號：G427文獻標識碼：A 文章編號：1992-7711（2014）04-044-1

眾所周知，培養學生的數學思維是數學教學中最有價值的部分，蘇聯數學教育學家斯托稱亞爾就明確指出：“數學教學是數學思維活動的教學。”隨著新課改的不斷深入，數學教學在培養學生理性思維的發展上有著其他學科不能比擬的優勢，這已經成為當前數學教師課堂教學關注的熱點。如何在數學教學中培養學生的數學思維？教師不妨從以下幾方面考慮。

一、抓本質，優化教學設計

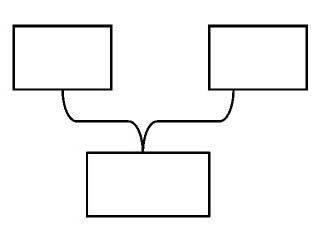
培養學生數學思維，就是要抓住對學生數學思維起關鍵性作用的知識，據此來優化課堂教學設計，讓學生清楚地透過知識的表面，挖掘深藏其背后的本質內涵。例如面對“有13個小朋友在捉迷藏，其中7個露著臉，問藏起來的有幾個？”這樣一年級的情境，老師通常會做這樣的設計教學：①老師問學生：你獲得什么數學信息？（生：有13個學生，能看到7個，要求藏起來幾個。）②師：猜一猜有幾個小朋友藏起來了？（生：6個。）③誰會列式？（生：13-7=6）④在學生回答正確后教師再問：還有誰再說一說。（生再重復說）⑤教師問：說說算式表示的意思是什么……我們有沒有對這司空見慣的教學場景產生過疑問：這里所體現的“數學味”在哪里呢？細細想來，這樣的教學只是調動了學生已有的知識經驗在進行解題，而學生在這一系列的過程之后還是停留在已經會的生活層面上，缺乏“數學化”的過程。事實證明，在做同樣類似的題目時還會有不少學生用加法計算，這說明學生還沒有真正掌握“知道總共的，求其中一部分要用減法”的數學含義。如果教學設計在第①問之后，加入這樣的圖示：

讓學生將獲得的信息放到適當的位置，再根據圖示來說題意列算式，學生就會借助圖將生活經驗進行捕捉、分析、加工、提煉成數學的條件和問題，從而達到對信息“數學化”的過程。在這一過程中，學生的認識經歷了模糊——清楚——深入的不斷提升，最終發展了學生的數學思維。

二、抓聯系，貫通知識整體

數學知識是一個環環相扣的有機整體，系統地掌握教材內容而不只是孤立的看待一個知識點，有利于學生對數學的整體認識，溝通知識網絡中相關知識點的聯系，可以為更高水平的思維活動作好充分的準備，我們可以用形象的“瞻前顧后”和“左顧右盼”這兩個成語形容知識間縱橫的關系。如“積的變化規律”一課，在學習過規律之后，教師出示這樣一組題：32×2=64，32×（2×4）=（）×4，32×（2×4）=（×）×4。在學生填完填空后注意觀察，發現一個因數（32）不變，另一個因數（2）乘4，原來的積（32×2）也乘4，從乘法結合律的角度對積的變化規律進行了溝通，充分體現了前后知識間聯系的內在統一性。這樣的課堂教學是一種高層次的綜合形式，帶給學生的或許是走出校門忘了作為知識的數學，卻深深銘刻著的數學思想與數學方法。

三、抓關鍵，關注教學細節

往往在課堂中，我們看到的流暢的教學過程只是代表著教師思考問題的過程，并不能真正代表學生的思維，而學生不是“一張白紙”，他們是帶著各自已有的知識經驗和需求，帶著各自學習的方式和習慣走入課堂之中的，教學必須尊重個體差異，這也可以從作業中那層出不窮的錯誤那里得到合理的解釋。這就需要我們教師的教學活動能體察入微，抓住內容的關鍵，體現細微差別，有針對性地開展教學。如教學“除數是小數的除法”一課，先出示一組對比題目：1200÷300=120÷30=12÷3=1.2÷0.3=……提問：①這些算式有什么特點？②如果讓你選其中的一個算式來列豎式，你會選哪一個，為什么？將學生的注意力有意識地集中于解題的核心——轉化。接著直接出示例題，學生在自己探索列豎式的方法時有可能會出現：①書中正確的豎式方法。②按照被除數化為整數的方法來移動小數點。③沒有移動小數點就計算的豎式。讓學生嘗試做題后讓學生進行有意義的探索和討論，說說究竟怎樣才能正確合理地處理小數點。在學生比較、思考中進行多種方法的辨誤、優化，從中歸納除數是小數的除法的一般方法。還要注意將學生自己不易察覺隱蔽著的知識盲點充分暴露，諸如對于3.9÷2.6=1.5，為什么除數和商都有小數點，那么被除數就應該有兩個小數點？讓學生辨清。這里整個的教學過程突出了兩個關鍵問題，一方面是知識結構中的關鍵，即知識的易錯點、重難點，另一方面是學生認知結構中的關鍵，即學生認知中的誤區和盲點。通過將視角聚焦于最關鍵處，一步步制造認知沖突，刺激學生思維惰性和打破機械模仿，這樣可以對課堂教學環節做深度開發，促進教師對教材的二次解讀，最大效益地促進學生數學思維的發展。

總之，立足數學課探尋多種培養學生數學思維的方法和途徑，使學生透過知識的“外殼”去引發思考，從而使學生的思維走向深刻，去體驗充滿數學的理性之美，切實提高學生的數學素養。