基于K均值聚類的高校圖書館勤工助學招聘
●孫雅楠,顧建新
(東南大學 情報科學技術研究所,南京 211189)
1 現行高校圖書館勤工助學招聘存在問題
勤工助學工作作為高校圖書館人力資源的一部分正在日益規范化、制度化。員工的招聘與選拔,是人力資源管理的開端,所以做好圖書館勤工助學招聘工作是圖書館人力資源管理的重要部分。現行的高校圖書館勤工助學招聘工作,基本是由學生向圖書館遞交申請書,圖書館調查學生家庭情況后,優先錄取貧困學生,進行簡單面試,根據其表現擇優錄取,錄取的學生分配給缺人的部門。在這個過程中,存在兩個問題:一方面,由于申請勤工助學的學生人數逐漸增加,面試過程中若沒有科學的記錄和比對系統支持,可能會由于橫向比較失真,導致不公平現象的發生;另一方面,忽略了學生的個性與崗位的適應性,崗位分配經驗化。傳統的勤工助學招聘是基于每個學生的初始能力差別不大的假設上,對不同崗位的學生進行相應培訓以適應崗位需求,但忽視了每個崗位對學生初始能力的個性需求。
為了解決以上問題,本文利用SPSS統計軟件的聚類分析方法,對高校圖書館的招聘數據進行科學處理,方便各個崗位個性化的擇優錄取,對改進圖書館的招聘工作,促使勤工助學崗位的招聘和安排更加公
平公正、科學合理。
2 基于K均值聚類的勤工助學招聘
2.1 聚類方法和K均值聚類
聚類分析就是將研究對象按照多個方面的特征進行綜合分類的一種統計方法。該方法通過將一個數據集劃分為若干組或類,并使得同一個組內的數據對象具有較高的相似度,而不同組內的數據對象則是不相似的。[1]K均值聚類方法是由MacQueen提出的解決聚類分析問題的一種經典算法,該算法具有原理簡單、速度快及能有效地處理大數據庫等優點,現已廣泛應用于數據挖掘和知識發現領域中。
2.2 K均值聚類應用于招聘工作的基本思路
K均值聚類方法應用于招聘工作,需要步驟如下。[2]
(1)對應聘學生集合X={x1,x2,…,xn},根據崗位能力需求等因素指派該集合中所有學生到k個類中來獲得初始聚類中心cj(I),I=1,j=1,2,…,k。
(2)計算每個應聘學生xi到每個聚類中心的距離D(xi,cj(I)),其中I=1,2,…,n;j=1,2,…,k。如果滿足D(xi,cj(I))=min{D(xi,cm(I))},m=1,2,…,k,則應聘學生xi∈Cj,表示該學生歸屬于第j類崗位。在該步驟中,距離的計算公式可采用歐氏距離,其定義如下:

其中:Xik表示第i個學生的第k個指標的觀測值
Xjk表示第j個學生的第k個指標的觀測值
dij表示第i個學生與第j個學生之間的歐氏距離
依次求出任何兩個點的距離系數dij(i,j=1,2,…,n)以后,則可形成一個距離矩陣:
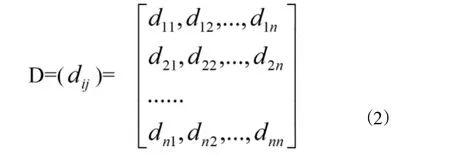
若dij越小,那么第i與j兩個樣品之間的性質就越接近。性質接近的樣品就可以或為一類。
(3)根據新的應聘學生劃分情況,計算k個新的聚類中心 ,其中nj是類別Cj中應聘學生的個數,x'是劃分到Cj中的數據元素。
(4)判斷Cj(I+1)是否等于Cj(I)或者誤差平方和(SSE)是否變化,若不相等或者SSE變化,則I=I+1,返回到步驟(2);若果相等或者SSE不變化,則完成了應聘學生的分類。
3 實例分析——以東南大學圖書館勤工助學招聘為例
3.1 招聘流程設計
東南大學李文正圖書館勤工助學招聘崗位有4個部門,分別是:采編部、流通閱覽部、信息咨詢部及系統與數字化建設部。現擬向本科一、二、三年級貧困生招聘16名勤工助學學生,根據實際招聘數據比例,分配到各個崗位分別為:(1)信息咨詢部4人;(2)系統與數字化建設部5人;(3)流通閱覽部5人;(4)文獻采編部2人。
具體的招聘辦法和程序如下。
(1)各年級推選。本科一、二、三年級根據學生的家庭情況和平時表現,共推選30人。
(2)筆試篩選。以《東南大學圖書館使用指南》中的基本內容作為考試范圍。根據考試分數的高低按1:1.25的比例,選擇20名學生進入第二階段的考試。
(3)面試評分。采訪圖書館各部門勤工助學管理負責人得到對學生助理四個維度的要求,分別為時間匹配度、計算機水平、應變能力、身體素質。選擇各部門老師組成招聘小組,根據招聘崗位對人員素質的要求,對進入面試考核階段的學生從上述四個維度進行考查,給出評分。
(4)綜合考慮筆試、面試成績,設計個性化方案,將合適人選分配到各個部門。[3]
3.2 利用SPSS統計軟件的K-Means Cluster方法對應聘學生進行聚類分析
為了簡化計算過程,提高聚類分析結果的準確性,采用SPSS 16.0軟件來取代繁雜的手工迭代。將20名學生的成績輸入SPSS進行聚類分析。首先,人工給出聚類分析計算的初始聚類中心。根據采訪各部門的實際情況,利用德爾菲法得出4個崗位中各個維度的權重,如表1所示,其中每一列代表擬將劃分的4個崗位類別,每一行分配各個維度的權重,該表顯示在算法開始時的初始聚類中心。
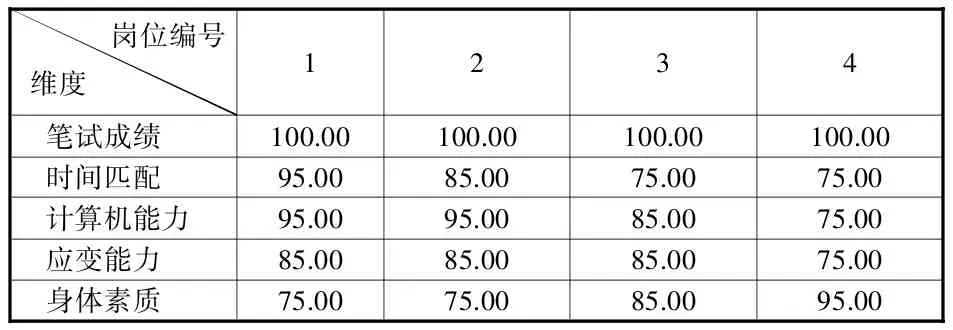
表1 初始聚類中心
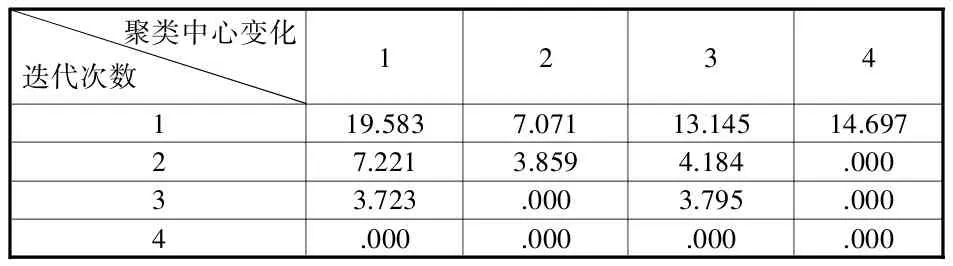
表2 迭代歷史記錄
3.3 聚類結果分析及錄取分配方案
表2顯示的是迭代歷史記錄。即,聚類的迭代計算過程。從中可以看出,在經過4次迭代后,聚類中心就不再發生變化,即誤差平方和的值在第4次計算后與上一次迭代計算結果的差值全部變為0,聚類計算到這里已經完成。[4]
表3顯示聚類分析的結果。其中的“聚類劃分”一列,表明每個應聘學生應屬的崗位類別,最后一列是每個應聘學生xi到其所屬類中心的距離D(xi,cj(I))。
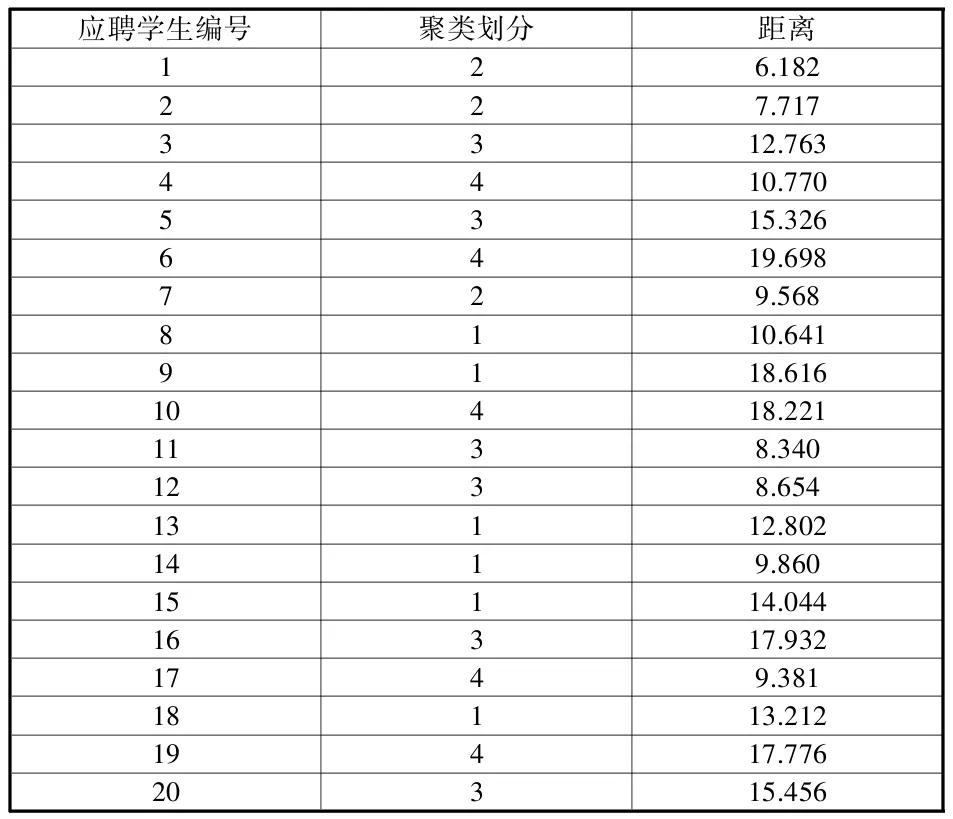
表3 聚類結果
對表3的聚類結果進行分析,在各崗位類別中根據各樣本到類中心點的距離依次從近到遠錄取;如果樣本到類中心點距離相同,則可參照筆試成績,得到如表4中的崗位分配結果。
4 總結
本文將圖書館的招聘工作與統計學知識相結合,希望找到一個科學便捷的方法進行勤工助學的招聘方法。這次嘗試雖然以數據分析為主,但為招聘工作提供了一個思路,為圖書館招聘公正合理提供了一個統計學理論支持。此外本文利用SPSS軟件的K均值聚類方法對應聘學生進行聚類分析有其便利性,但分析不夠全面,在實際招聘中可以嘗試更多的方法,考慮到更全面的因素。
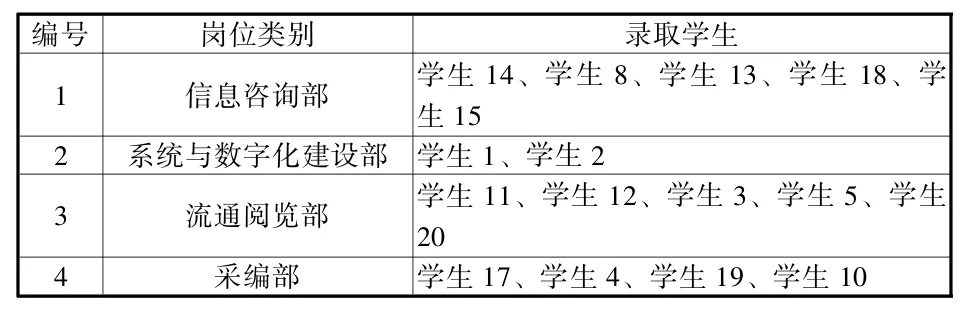
表4 崗位分配結果
[1]鄧海燕.聚類分析與判別分析的區別[J].武漢學刊,2006(1):29-31.
[2]寧凱.基于K均值聚類的編組站分類方法研究[J].鐵路運營技術,2011(7):41-46.
[3]沈炎.SPSS在高校圖書館勤工助學招聘中的應用[J].大學圖書情報學刊,2008(6):33-35.
[4]顧榮炎.SPSS 12.0 For Windows實用教程與操作技巧[D].上海:上海科學技術文獻出版社,2005,9.

