二粒子未知態的受控量子通信

王作棟，黃亦斌

(江西師范大學物理與通信電子學院，江西 南昌330022)

0 引言

1993年，Bennett等人提出了一種利用Bell態進行量子隱形傳態的方案［1］，自從該方案被提出來后，人們又提出了利用其它糾纏態作為量子信道的量子通信方案［2～5］。1999年，Hillery等人提出了一種量子信息分裂方案(Quantum information splitting簡稱:QIS)［6］，在該量子信息共享方案中，發送者通過量子隱形傳態將未知態分發給多個接收者，任何一個接收者都可以在發送者的控制下恢復該未知態。所以，量子信息分裂(QIS)方案也是一種多方受控的量子隱形方案［7］。

本文提出了一個利用7粒子態作為量子信道的多方受控的量子通信方案。根據不可克隆原理，發送者Alice不可能復制未知態，即不可能使接收者Bob和Charlie同時接收到該未知態。在本文中，Alice要將一個2粒子未知態發送給Bob和Charlie。Diana為控制者，不具備接收未知態的能力，但是她能夠控制接收者重構二粒子未知態。Alice對自己擁有的4個粒子做一次 von-Neumann聯合測量［8］，控制者在計算基下對他的粒子做測量。接收者Bob和Charlie可以根據2次測量結果對自己擁有的粒子做相應的幺正操作，就可以重構Alice所發送的未知態。

假如在建立量子信道時，將Diana的粒子發送給Charlie。Charlie手中有3個粒子，她既是接收者又是控制者，她能夠單獨得接收Alice所發送的未知態，又能夠控制Bob接收未知態。所以說Charlie對于未知態的恢復能力是強于Bob的，這在某種程度上實現了分級量子信息通信［9～11］。

1 二粒子未知態的受控量子隱形傳態

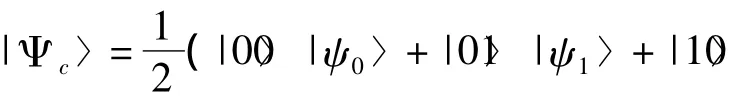
發送者Alice制備大量7粒子態其中，|ψ0〉，|ψ1〉，|ψ2〉，|ψ3〉是任意的5 bit量子態，它們之間是相互正交:

Alice作為發送者，它把每一個7粒子態的1、2粒子留在自己手中;3、4粒子發送給Bob;第5、6個粒子發送給Charlie;第7個粒子發送給Diana。

Alice想要傳輸一個2粒子未知態|Ψs〉給接收者，這個2粒子未知態為:

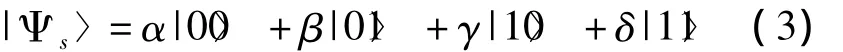
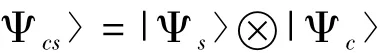
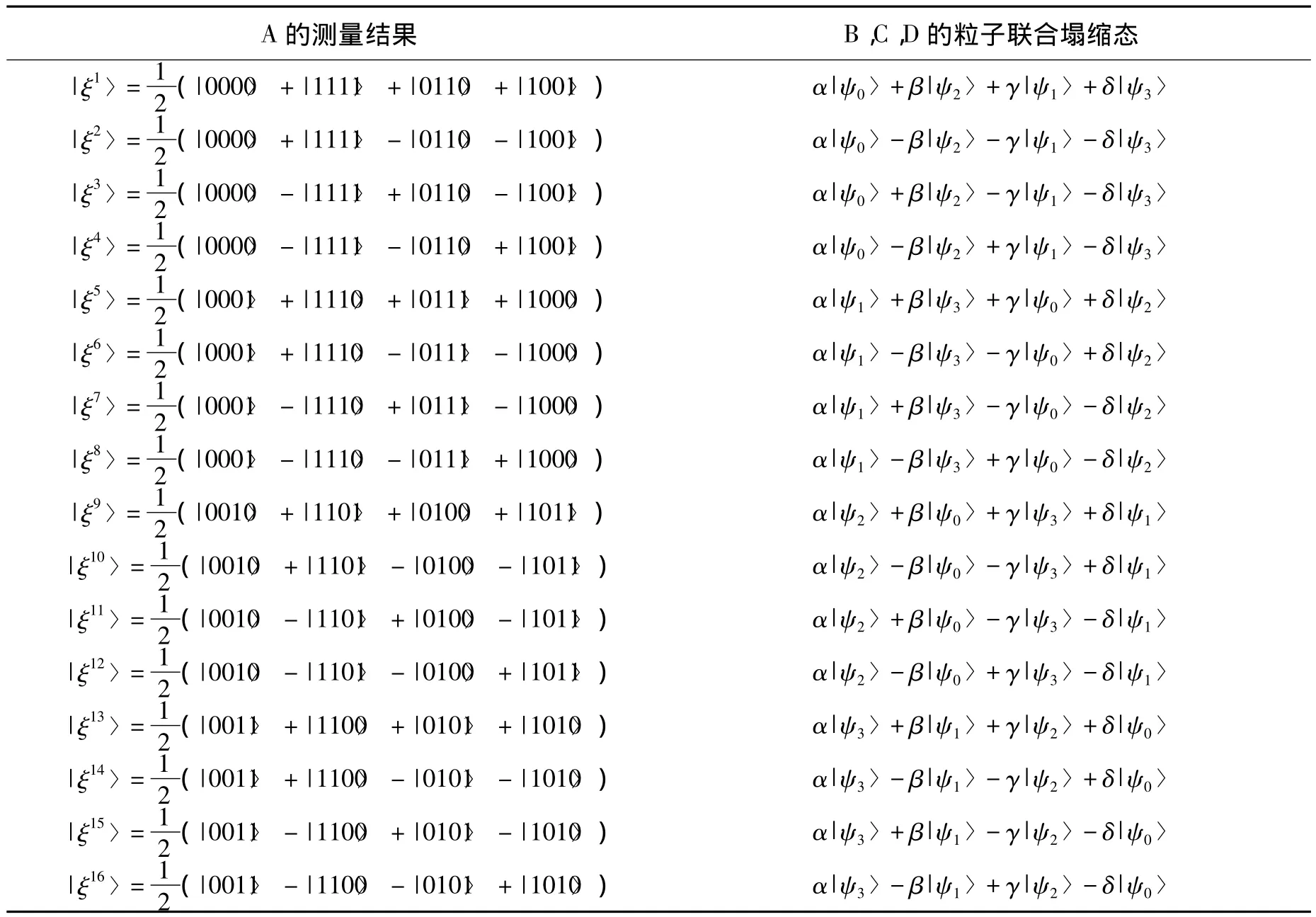
表1 Alice的測量結果與Bob、Charlie和Diana三者的粒子聯合塌縮態的關系

如果讓Bob接收信息，那么發送者Alice把她的測量結果發送給Bob。其次，控制者Diana對她手中的粒子在計算基上做一次測量，然后她也把測量結果發送給Bob。最后，Bob根據接收到的2個測量結果，經過適當的幺正操作就可以重構發送者Alice所發送的未知態。詳細測量結果，測量后的塌縮態，接收者所要做的幺正操作見表2。

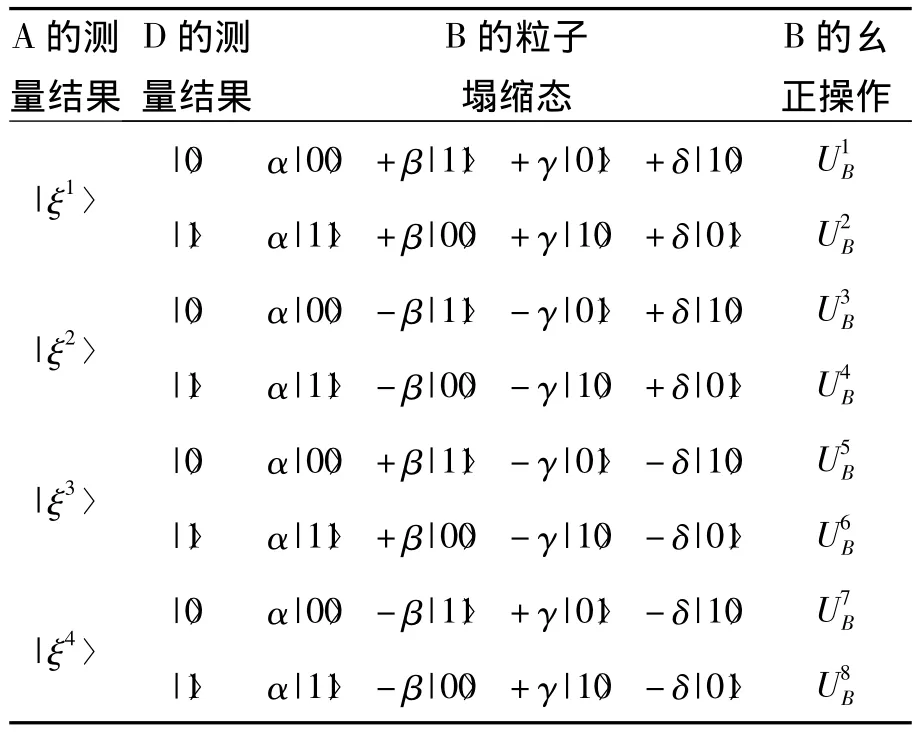
表2 Bob根據Alice和Diana的測量結果做適當的幺正操作便可以重構2粒子未知量子態

其中:Bob在基{|00〉，|01〉，|10〉，|11〉}下，所要做的幺正操作分別為:

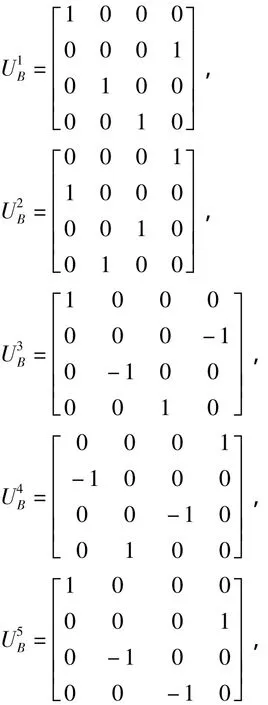
因為文章篇幅所限，只對當Alice的測量結果為|ξi〉(i=1，2，3，4)的情況進行了討論。

如果讓Charlie接收信息，那么發送者Alice把她的測量結果發送給Charlie。其次，控制者Diana對她手中的粒子在計算基上做一次測量，然后她也把測量結果發送給Charlie。然后Charlie根據接收到的2個測量結果，經過適當的幺正操作就可以重構發送者Alice所發送的量子信息。Alice向Charlie發送2粒子未知態的過程，與向Bob發送的情況完全類似，不再做詳細的列舉。

2 Charlie是更高級接收者的方案

Alice建立量子信道分配信道粒子時，將原本應該屬于 Diana的粒子發送給 Charlie。此時Charlie手中有3個粒子，他既是接收者又是控制者。她收到Alice的測量結果以后，對自己手中的第3個粒子在計算基上做一次測量，根據測量結果她能夠單獨地接收Alice所發送的未知態。如果Alice想要把未知態發送給Bob，此時Charlie只需要對他的第3個粒子在計算基上做一次測量并把測量結果發送給Bob，Bob接收到Alice和Charlie的測量結果，經過適當的幺正操作就可以重構發送者Alice所發送的未知態。所以說Charlie對于未知態的恢復能力是強于Bob的，這在某種程度上實現了分級量子信息通信。

3 結論

上文詳細描述了一個利用7粒子態實現2粒子未知態的受控量子隱形傳態方案。在該方案中，發送者Alice與接收者Bob、Diana和控制者Charlie共享一個7粒子態。接收者Bob和Charlie都能夠接收到未知態，但是他們必須有控制者Diana的協助。

如果設定A為發送者，B1，B2，B3…為接收者，C為控制者。那么就可以建立一個1對N(N≥1)的受控量子通信網絡。如果C既想控制B接收未知態又想接收到二粒子未知態，則C在建立量子信道時至少要分配到3個粒子。

［1］ Bennett C H，Brassard G，Crépeau C，et al.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels［J］.Phys Rev Lett，1993，70:1895-1899.

［2］ Shi B S，Jiang Y K，Guo G C.Probabilistic teleportation of two-particle entangled state［J］.Phys Lett A，2000，268:161-164.

［3］ Cao Z L，Yang M，Guo G C.The scheme for realizing probabilistic teleportation of atomic states and purifying the quantum channel on cavity QED［J］.Phys Lett A，2003，308:349-354.

［4］ 鄭亦莊，戴玲玉，郭光燦.三粒子糾纏W態的隱形傳態［J］.量子電子學報，2004，21(6):730-733.

［5］ 洪智慧，聶義友，李嵩松，等.四粒子團簇態的量子隱形傳態［J］.江西師范大學學報(自然科學版)，2007，31(5):459-562.

［6］ Hillery M，Buzek V，Berthiaume A.Quantum secret sharing［J］.Physical Review A，1999，59:1829-1834.

［7］ Shukla C，Pathak A.Hierarchical quantum communication［J］.Physics Letters A，2013，377:1337-1344.

［8］ 肖仕敏，李淵華，桑明煌，等.基于5粒子團簇態實現2粒子未知態的量子隱形傳態［J］.江西師范大學學報(自然科學版)，2012，(4):370-372.

［9］ Wang X W，Xia L X，Wang Z Y，et al.Hierarchical quantum-information splitting［J］.Opt Comm.，2010，283:1196-1199.

［10］Wang X W，Zhang D Y，Tang S Q，et al.Multiparty hierarchical quantum-information splitting［J］.J Phys B: At Mol.Opt.Phys.，2011，44:035505.

［11］Wang X W，Zhang D Y，Tang S Q，et al.Hierarchical quantum information splitting with six-photon cluster states［J］.Inter J Theor Phys.，2010，49:2691-2697.