雙轉(zhuǎn)子永磁電動機有限元分析

王淑紅，呂 航，武 瀟，趙曉春

(太原理工大學，太原030024)

0 引 言

雙轉(zhuǎn)子永磁直流電機由內(nèi)轉(zhuǎn)子(電樞轉(zhuǎn)子)和外轉(zhuǎn)子(永磁體轉(zhuǎn)子)組成。運行時，兩個轉(zhuǎn)子受到耦合場的電磁轉(zhuǎn)矩為等大小反方向的相互作用轉(zhuǎn)矩，使兩個轉(zhuǎn)子朝相反的方向旋轉(zhuǎn)［1］。因此電機的固定部分不承受電磁轉(zhuǎn)矩，可明顯提高機身的平穩(wěn)性，在船艦推進系統(tǒng)中有廣闊應(yīng)用前景［2］，針對對轉(zhuǎn)結(jié)構(gòu)永磁直流電動機的性能進行研究尤為重要。

文獻［3］使用有限元法對傳統(tǒng)單轉(zhuǎn)子永磁直流電機進行了建模分析，簡要討論了電機結(jié)構(gòu)上的各參數(shù)對性能的影響。文獻［4］以抑制轉(zhuǎn)矩波動為目標對傳統(tǒng)永磁直流電機進行了優(yōu)化設(shè)計，使用有限元法對優(yōu)化結(jié)果進行了檢驗。目前對于雙轉(zhuǎn)子永磁直流電動機的有限元研究文獻較少。本文分別就靜態(tài)特性與動態(tài)特性對雙轉(zhuǎn)子永磁直流電動機進行了有限元分析;并采用重疊換相方法，改變控制主電路中開關(guān)管提前導通角，找到了使電磁轉(zhuǎn)矩波動范圍減小的最佳提前導通角。減小了穩(wěn)定運行過程中的電磁轉(zhuǎn)矩脈動率。

1 靜態(tài)有限元模型的建立

圖1 雙轉(zhuǎn)式永磁電動機結(jié)構(gòu)

2 靜態(tài)性能分析

對有限元模型計算之后能夠得到靜態(tài)特性，包括靜磁場分布情況和一對極范圍內(nèi)特定激勵方式下電機靜轉(zhuǎn)矩特性Te=f(i，θ1，θ2)，與電感特性L =f(i，θ1，θ2)。

2.1 磁場分布

圖2 為兩個不同相對位置處靜態(tài)磁密分布圖。B 相繞組中通以30 A 的正向電流，C 相繞組通相等大小的反向電流。圖2(a)為初始位置處磁密分布圖，可以看出12 個磁極分界線處的外轉(zhuǎn)子圓鋼磁密達到了高度飽和，為1.76 ～1.89 T 之間。每個磁極中心線附近的內(nèi)轉(zhuǎn)子齒磁密也較高，為1.63 ～1.76之間。圖2(b)為兩個轉(zhuǎn)子相對位置為15°時磁密分布圖，該時刻外轉(zhuǎn)子(永磁體轉(zhuǎn)子)順時針轉(zhuǎn)過約10°，內(nèi)轉(zhuǎn)子(電樞轉(zhuǎn)子)逆時針轉(zhuǎn)過約5°。由圖可得磁密分布不僅整體上跟隨永磁體轉(zhuǎn)子轉(zhuǎn)過了相應(yīng)的角度，每極周期內(nèi)的分布情況也存在一定的差別。

圖2 不同相對位置處磁通密度分布圖

2.2 靜轉(zhuǎn)矩特性曲線

取A 相正向繞組處于S 極的中心線處為初始位置，兩個轉(zhuǎn)子相對位置(θ1-θ2)的變化范圍為一對極。在繞組激勵不變的條件下，計算不同相對位置處數(shù)據(jù)可得到靜轉(zhuǎn)矩特性曲線。再依次改變激勵大小可得到如圖3 所示一簇靜轉(zhuǎn)矩特性曲線。

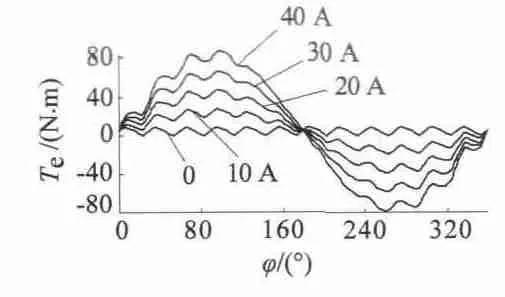
圖3 靜轉(zhuǎn)矩特性曲線

圖3 中，電流為0 時的特性曲線表示的是齒槽轉(zhuǎn)矩，波動周期個數(shù)與一對極下的齒數(shù)相符，齒槽轉(zhuǎn)矩是引起電機轉(zhuǎn)矩脈動的主要因素。由圖可得，各位置處靜轉(zhuǎn)矩值減去該位置處的齒槽轉(zhuǎn)矩值之后基本與電流大小成正比，與永磁體勵磁方式下靜轉(zhuǎn)矩變化規(guī)律一致。但是在少數(shù)位置處，當激磁電流超過30 A 之后，靜轉(zhuǎn)矩值稍低于對應(yīng)理論上的正比值。這是由于該位置處磁路已經(jīng)飽和，電樞反應(yīng)引起每極下主磁通平均值稍有下降，因此該位置處的靜轉(zhuǎn)矩稍低于理論正比值。

2.3 電感特性曲線

根據(jù)不同條件下的A 相自感值可得如圖4 所示的自感特性曲線簇。

圖4 自感系數(shù)變化曲線

由圖4 可知，繞組中電流為0 時，自感系數(shù)隨相對位置不同變化不大，繞組的自感系數(shù)近似為常數(shù)，控制系統(tǒng)設(shè)計時電機參數(shù)可以認為是常數(shù)。而當激磁電流變化時，特別是電流較大、轉(zhuǎn)子相對位置變化時，某些相對位置處磁路飽和，繞組自感系數(shù)隨轉(zhuǎn)子位置不同，是近似階梯形的曲線，并且階梯的平頂部分都在相對位置90° ～270°的范圍內(nèi)，自感值也很接近。其他位置范圍內(nèi)的自感值隨著電流值的增大而基本均勻減小，超過30 A 后隨電流值變化的幅度略微降低。

根據(jù)不同條件下的A 相與B 相互感值，可得如圖5 所示的互感特性曲線簇。

在數(shù)學模型研究及試驗驗證方面，波蘭科學院[22]建立了蓄熱換向流動反應(yīng)器(TFRR)的一維模型的2個不同版本(①帶反應(yīng)器壁蓄熱與②無反應(yīng)器壁蓄熱)，并通過大尺寸反應(yīng)器上的試驗數(shù)據(jù)對模型進行了驗證。研究認為壁面蓄熱并不會直接影響反應(yīng)器內(nèi)填料溫度分布規(guī)律。

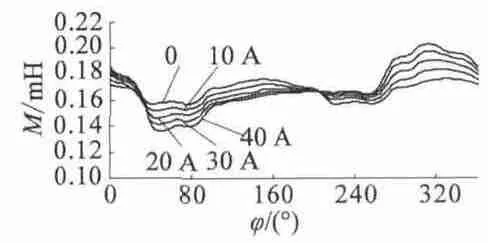
圖5 互感系數(shù)變化曲線

3 動態(tài)有限元模型的建立

動態(tài)有限元模型的電機結(jié)構(gòu)、繞組分相與靜態(tài)模型相同，可沿用靜態(tài)模型。此外，動態(tài)模型的激勵形式為外接控制電路激勵，并且需要將兩個轉(zhuǎn)子定義為獨立的運動區(qū)域同時進行運算。Maxwell 2D 模塊支持多個運動部分同時運算，本文在此模塊下進行電機的動態(tài)有限元建模。

3.1 動態(tài)模型激勵設(shè)置

動態(tài)模型的外接控制電路需要給繞組提供根據(jù)內(nèi)轉(zhuǎn)子和外轉(zhuǎn)子的相對位置參數(shù)而周期變化的方波激勵［1］，這樣可保證電樞磁場與永磁體磁場等效同步，推動內(nèi)轉(zhuǎn)子和外轉(zhuǎn)子沿著各自的方向運動。圖6 為有限元計算模型中電機的主電路。通過控制主電路中的六個壓控開關(guān)管，使繞組根據(jù)相對位置參數(shù)而按既定規(guī)律通斷。主電路圖中與各相繞組相串聯(lián)支路上的電阻RA，RB，RC為相繞組電阻(三相繞組對稱，RA=RB=RC=R)，電感LA，LB，LC為每相繞組的端部漏感(LA= LB= LC= Lδ)，均可通過Ansoft 軟件RMxprt模塊下直流電機快速建模得到:R =0.17Ω，Lδ=6.931 8 ×10-5H。圖中，LWA是有限元模型A 相繞組。

圖6(b)為主電路中壓控開關(guān)管的控制電壓檢測電路。本文中設(shè)置檢測電壓高于0.5 V，即觸發(fā)該檢測表所對應(yīng)的開關(guān)管導通，低于0.5 V 即關(guān)斷。以A 相繞組的輸入端壓控開關(guān)管S1 為例，S1 所對應(yīng)檢測支路中脈沖信號VP1周期為60°，脈沖寬度為20°，電壓下限為0，上限為1 V，上升沿位置為5°，控制信號為θ1-θ2(θ1為內(nèi)轉(zhuǎn)子位置變量，θ2為外轉(zhuǎn)子位置變量)。相對機械位置的周期60°內(nèi)，A 相正向?qū)ǚ秶鸀?° ～25°。分別設(shè)置各個開關(guān)管對應(yīng)的檢測支路中脈沖信號，使S2 ～S6 所對應(yīng)的脈沖信號依次比前一個延后10°。采用兩相同時通電方式，若A+C-表示A 相正向和C 相反向?qū)ǖ臓顟B(tài)，則一周期內(nèi)繞組導通狀態(tài)依次為A +C -，B +C-，B+A-，C+A-，C+B-，A+B-。

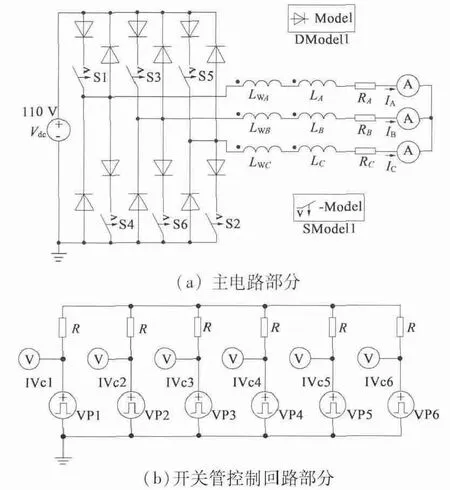
圖6 使用Maxwell 編輯的外電路

3.2 運動區(qū)域設(shè)置

相對于單轉(zhuǎn)子旋轉(zhuǎn)電機，雙轉(zhuǎn)子直流電動機的機械運動部分的設(shè)置較特殊，對雙轉(zhuǎn)子電機的動態(tài)性能有限元計算論文較少。對本文所研究的雙轉(zhuǎn)子直流電動機而言，兩個轉(zhuǎn)子的機械運動部分是各自獨立的，應(yīng)為兩個轉(zhuǎn)子分別設(shè)置運動求解區(qū)域(Band)。建立能恰好包含內(nèi)轉(zhuǎn)子的面域，設(shè)為Band1;建立恰好包含外轉(zhuǎn)子的面域，設(shè)為Band2，如圖7 所示(圖中陰影部分為各自的Band 區(qū)域)。

圖7 運動區(qū)域設(shè)置圖

運動區(qū)域內(nèi)物體的運動方式都設(shè)定為繞Z 軸的旋轉(zhuǎn)運動，并分別載入計算所得的轉(zhuǎn)動慣量，內(nèi)轉(zhuǎn)子轉(zhuǎn)動慣量為0.064 6 kg·m2，外轉(zhuǎn)子轉(zhuǎn)動慣量為0.034 1 kg·m2。

4 動態(tài)性能分析

雙轉(zhuǎn)子永磁直流電動機動態(tài)性能包括:起動過程及穩(wěn)定運行時繞組電流、內(nèi)轉(zhuǎn)子和外轉(zhuǎn)子各自的電磁轉(zhuǎn)矩、轉(zhuǎn)速隨時間變化曲線。

4.1 電流變化曲線

從電樞繞組的電流方程、電壓平衡方程來看，對轉(zhuǎn)式永磁直流電動機等效電路與傳統(tǒng)無刷永磁直流電動機一致，可借助傳統(tǒng)單轉(zhuǎn)子電機的電路平衡關(guān)系來分析該電機電樞電流。

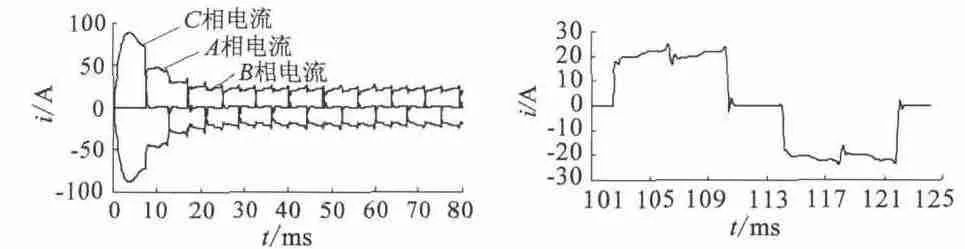
圖8 電流曲線

在三相六狀態(tài)工作方式下，每時刻均為兩相繞組導通，另一相為續(xù)流狀態(tài)或者完全關(guān)斷狀態(tài)，如圖8(a)所示。若取一相繞組的一次續(xù)流過程和完全關(guān)斷過程為一個換相周期，則電機運行過程可完全由三相的換相周期輪流組成。以A+C-狀態(tài)轉(zhuǎn)換至B+C-狀態(tài)的換相周期為例，此換相周期可分為A 相續(xù)流過程t1和A 相完全關(guān)斷過程t2組成。根據(jù)續(xù)流過程等效電路可得續(xù)流過程中電流方程式如下［5］:

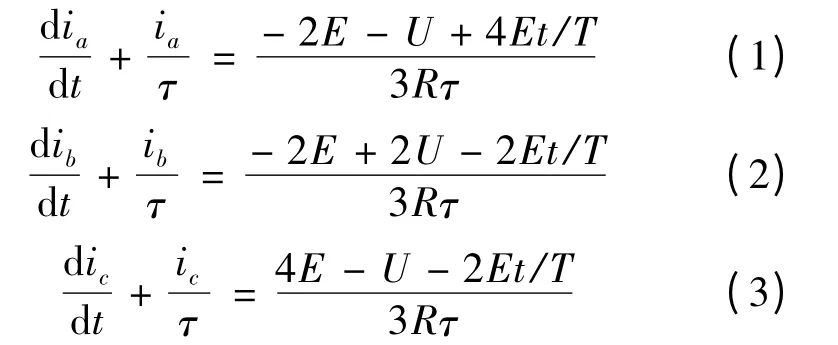
式中:τ 為相繞組電磁時間常數(shù);R 為相繞組電阻;I0為換相過程A 相初始電流;U 為輸入到逆變器的直流電源電壓;E 為相繞組等效反電勢幅值。有限元計算所得電機穩(wěn)定運行時相繞組反電勢波形如圖9所示，圖中曲線為相對轉(zhuǎn)速穩(wěn)定在430 r/min 時一個電周期內(nèi)相繞組反電勢波形。曲線在齒槽效應(yīng)影響下具有多次波動。為方便公式計算，將反電勢波形等效為規(guī)則120°梯形波。上式中，反電勢幅值E為等效梯形波幅值，不能取原波形的波動峰值。

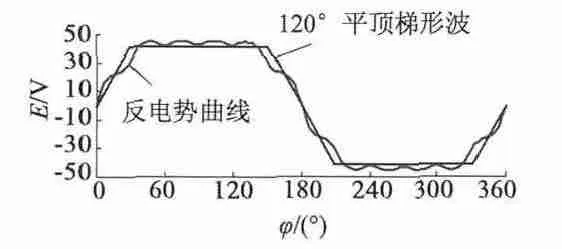
圖9 相繞組反電勢波形

根據(jù)式(1)至式(3)，令初始條件:ia(0)=I0，ic(0)= -I0，ib(0)=0。求取微分方程，可得A 相繞組電流降為零，所需的時間t1與t1時刻結(jié)束時B 相和C 相電流值表達式:

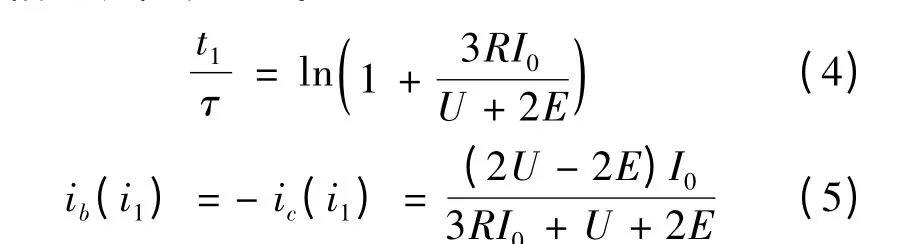
由式(4)、式(5)可得t1=0.25 ms，ib(i1)=16.9 A;與圖4 中的數(shù)據(jù)t1=0.2 ms，ib(i1)=17.2 A 基本吻合。其中t1的差別是由于時間段t1很短暫且與Maxwell 中的計算步長0.2 ms 相仿，因而等效為一個步長。由計算結(jié)果可知，由于電流變化率的不同，繞組由導通到電流下降至零的時間很短暫，而此時新導通相的電流尚未上升到平均導通電流［6］，因此續(xù)流過程的三相電流值大小均會小于其他時間的電流值。

4.2 電磁轉(zhuǎn)矩曲線

轉(zhuǎn)矩脈動率有以下定義［7］:

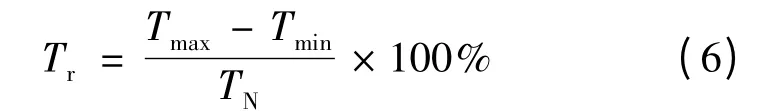
式中:Tmax為電磁轉(zhuǎn)矩最大值;Tmin為電磁轉(zhuǎn)矩最小值;TN為電磁轉(zhuǎn)矩穩(wěn)定運行的平均值。

電機起動到穩(wěn)定運行過程中，兩個轉(zhuǎn)子所受的電磁轉(zhuǎn)矩曲線如圖10(a)所示。

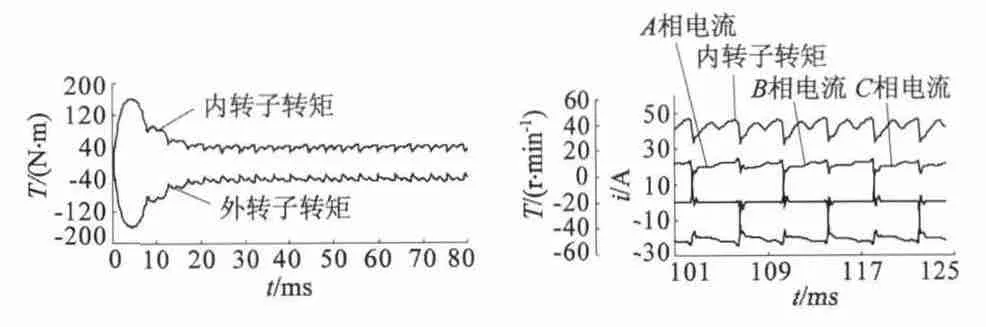
圖10 電磁轉(zhuǎn)矩曲線

由圖10 可知，內(nèi)轉(zhuǎn)子與外轉(zhuǎn)子所受電磁轉(zhuǎn)矩時刻大小相等方向相反。根據(jù)式(6)計算可得穩(wěn)定運行過程的轉(zhuǎn)矩脈動率Tr=43.1%，每電周期內(nèi)有12 次波動，對應(yīng)于一對極范圍下的12 組齒槽;其中有6次達到最小值并且均出現(xiàn)在關(guān)斷相的續(xù)流過程中。

穩(wěn)定運行過程中，一個電周期內(nèi)繞組電流與內(nèi)轉(zhuǎn)子所受電磁轉(zhuǎn)矩的曲線如圖10(b)所示。電磁轉(zhuǎn)矩的最小值均出現(xiàn)在續(xù)流過程中。根據(jù)電流曲線的分析結(jié)論可知，續(xù)流過程中續(xù)流相電流已降為零，新導通相電流還未增加至穩(wěn)定值，換相過程中電磁轉(zhuǎn)矩會減小［8］。并且正在換相的兩相繞組也正處于氣隙磁密較小的位置，因而電樞繞組所受的總電磁轉(zhuǎn)矩降至轉(zhuǎn)矩脈動的最低值。

4.3 轉(zhuǎn)速曲線

電機起動到穩(wěn)定過程中，兩個轉(zhuǎn)子的轉(zhuǎn)速曲線如圖11 所示。在30 ms 時刻到達穩(wěn)定轉(zhuǎn)速，內(nèi)轉(zhuǎn)子為150 r/min，外轉(zhuǎn)子為280 r/min。兩個轉(zhuǎn)子穩(wěn)定轉(zhuǎn)速的比值為0.536，轉(zhuǎn)動慣量比值為1.894，兩者之積為1.015≈1。因此兩個轉(zhuǎn)子負載轉(zhuǎn)矩相同的情況下，穩(wěn)定轉(zhuǎn)速的大小與各自的轉(zhuǎn)動慣量基本成反比。

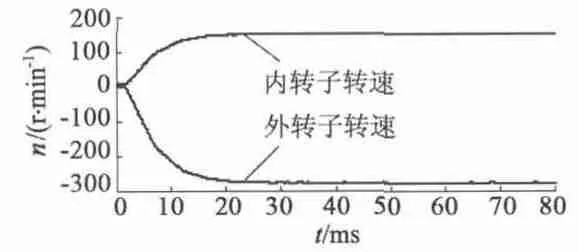
圖11 轉(zhuǎn)速曲線

5 轉(zhuǎn)矩脈動抑制

由圖10(b)的電磁轉(zhuǎn)矩分析結(jié)果可得，在繞組換相的續(xù)流過程中，所引起的轉(zhuǎn)矩波動較之齒槽轉(zhuǎn)矩波動影響更大。采取措施減小換相轉(zhuǎn)矩脈動將明顯提高轉(zhuǎn)矩整體平穩(wěn)性。而選擇適當?shù)奶崆皩ń嵌龋?］，使續(xù)流繞組與將要導通的繞組重疊導通，可以補償續(xù)流過程中的電流值下降，減小凹下的電磁轉(zhuǎn)矩波動［10］。如果提前導通角度過大，則會引起新的轉(zhuǎn)矩波動［11］，因此必須在合適的提前導通角下才能有效減小轉(zhuǎn)矩波動。文獻［12］提出了針對不同換相過程中提前導通角(時間)的計算方法。在4E＞U 的條件下，電機運行在高速段，此過程中換相時間可表示:

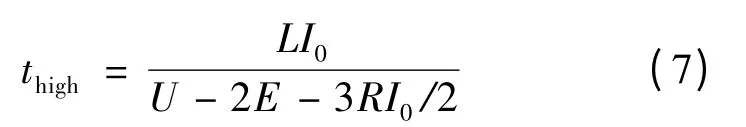
式中:L 為繞組等效電感，等于相繞組自感與繞組間互感之差。由式(7)計算出換相區(qū)間時間并換算為角度，該值的一半為最佳提前換相角，為2.2°。在有限元軟件Maxwell 2D 環(huán)境下可通過改變開關(guān)管控制回路來模擬換相繞組提前導通。將控制回路中每個脈沖信號的上升沿根據(jù)相應(yīng)的提前導通角前移并維持下降沿不變，可改變各脈沖信號所對應(yīng)的MOS 管導通范圍，實現(xiàn)繞組提前導通。通過比較2.2°左右的不同提前導通角下有限元分析結(jié)果發(fā)現(xiàn)，提前導通2°時電磁轉(zhuǎn)矩波動最小。在這種方案下壓控開關(guān)管S1 的導通區(qū)間為3°～25°，S2 ～S6 各自的導通區(qū)間依次比前一個延后10°。以A+C-狀態(tài)轉(zhuǎn)換至B+C-狀態(tài)的換相過程為例，將出現(xiàn)23°～25°的三相同時導通區(qū)間，這就形成了重疊換相。圖12 為有限元計算所得不采用提前導通與采用提前導通(提前導通角為2°)時兩個轉(zhuǎn)子的電磁轉(zhuǎn)矩曲線比較圖，由圖12 可得穩(wěn)定運行過程中電磁轉(zhuǎn)矩脈動率Tr=27.9%，與不采用重疊換相相比減小了15.2%。

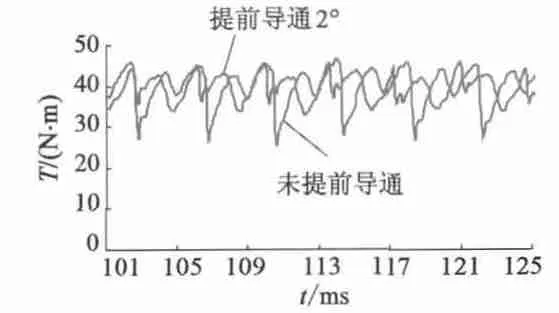
圖12 電磁轉(zhuǎn)矩曲線比較圖

6 結(jié) 語

本文建立了雙轉(zhuǎn)子永磁直流電動機的電磁場有限元模型，使用有限元分析軟件Maxwell 2D 模塊分別對電機靜態(tài)性能和動態(tài)性能進行了分析。通過靜態(tài)仿真繪制了磁場分布與靜態(tài)特性曲線，為優(yōu)化電機結(jié)構(gòu)參數(shù)與分析電機特性提供了理論依據(jù)。通過動態(tài)仿真實驗得到了各參數(shù)的運行規(guī)律，并得到了減小電磁轉(zhuǎn)矩波動的最佳提前導通角，為電機控制策略的優(yōu)化提供了基礎(chǔ)。

［1］ 張世勤，邱建琪. 雙轉(zhuǎn)式永磁無刷直流電動機的建模與仿真［J］.中國電機工程學報，2004，24(12):176 -181.

［2］ 孫希通，王育才.雙轉(zhuǎn)式永磁無刷直流電動機系統(tǒng)建模與仿真［J］.電機技術(shù)，2009(3):1 -4.

［3］ 王瑞，高尚.永磁無刷直流電機電磁場有限元分析［J］.電子技術(shù)，2011(5):69 -71.

［4］ 連軍強，謝順依.基于有限元的永磁無刷直流電機轉(zhuǎn)矩優(yōu)化設(shè)計［J］.電機與控制應(yīng)用，2011，38(12):7 -12.

［5］ 譚建成.永磁無刷直流電機技術(shù)［M］.北京:機械工業(yè)出版社，2011.

［6］ 包向華，章躍進.無刷直流電動機換相轉(zhuǎn)矩脈動的分析和削弱方法［J］.微特電機，2007，35(2):14 -17.

［7］ 孫建忠，白鳳仙.特種電機及其控制［M］.北京:中國水利水電出版社，2005.

［8］ 李懷兵，丑武勝.換相期間無刷直流電機轉(zhuǎn)矩脈動的抑制策略［J］.電機與控制應(yīng)用，2011，38(11):20 -24.

［9］ 劉會飛，王淑紅.無刷直流電動機轉(zhuǎn)矩脈動的抑制［J］.電力學報，2006，21(2):157 -159.

［10］ YOSHIDAM M. Noise reduction by torque ripple suppression in brushless DC motor［C］//Proceedings Form PESC Record.1988:1397 -1401.

［11］ 王淑紅，熊光煜.無刷直流電機換相轉(zhuǎn)矩脈動減小及動態(tài)仿真［J］.電機與控制學報，2008，12(2):169 -173.

［12］ 羅宏浩，吳峻.永磁無刷直流電機換相控制研究［J］. 中國電機工程學報，2008，28(24):108 -112.