基于氣隙磁場測定的永磁球形電動機位置檢測方法研究

馬 姍，李國麗，錢 喆，王群京，過希文，劉阿娟

(1.安徽大學，合肥230601;2.安徽安納達鈦業股份有限公司，銅陵240024)

0 引 言

多自由度運動系統有著廣泛的運用，比如機器人機械臂、紅外與激光跟蹤系統、自動化制造等。當前的多自由度運動系統由單個自由度驅動和傳動機構實現，系統龐大、復雜。由于受轉動慣量、間隙、非線性摩擦和齒輪彈性形變等因素影響，難以獲得高的動態性能。隨著對多自由度執行機構動態和穩態性能的要求日益提高，科研人員積極參與研制具有多自由度運動功能的精密執行器。Lee K M 等人提出了變磁阻型球形步進電動機［1］，Wang J，Jewell G W 提出了兩自由度電機［2-3］，Kahlen K 和Week E M等人研發了一種三自由度永磁球形電動機［4-5］。國內也積極推進多自由度電動機的研究。比如，蘇仲飛、劉昌旭等人設計出無刷直流球形電動機［6］;黃聲華等人提出雙饋感應球形電動機［7-8］;程樹康、蔡鶴皋等人設計研制了非球形結構的正交圓柱結構三自由度電機［9-10］，夏長亮、李洪鳳、郭辰等提出了基于Halbach 陣列的永磁球形電動機［11-13］。

為了達到精確控制多自由度電機的目的，需要實時掌握轉子的位置。文獻［14］中，Lee K M 提出了采用一套由兩個半圓形滑軌支架、固定輸出軸和3 個旋轉編碼器組成的滑軌支架測量系統來檢測轉子位置的方法。該方法引入了轉子與導軌相連接產生的摩擦，影響轉子的定位精度。Chirikjian G S 等人提出了基于光電傳感器的轉子位置檢測方法［15-16］;王群京、錢喆等人提出了基于機器視覺的永磁球形步進電動機的轉子位置檢測方法［17］，這些方法雖然克服了接觸式測量帶來的摩擦，但測量原理和結構復雜，而且難以實現實時位置檢測。

本文提出了基于永磁體作磁源、通過三個固定檢測點檢測到的三維磁感應強度數據來計算轉子位置的方法。

1 檢測基本原理

置于轉軸上的永磁體隨轉軸轉動時，永磁體將在其周圍建立一個穩態磁場。而轉軸相對于參考坐標系的方位信息，包含在空間固定點的磁感應強度數據中。圖1 展示了坐標系中一個長度l，半徑α，均勻軸向磁化且剩余磁感應強度為M0的圓柱永磁體。永磁體中心點Pm至坐標原點的距離為Lm。永磁體所在軸線與z 軸的夾角以及軸線在xoy 平面上的投影與x 軸的夾角分別為θ 與φ。z 軸上PS點的坐標為(0，0，Ls)，將PS點的磁感應強度B 分解為平行轉軸方向的Bl和垂直轉軸方向的Bρ，則PS點x 軸方向的磁感應強度Bx和y 軸方向的磁感應強度By與Bl和Bρ的關系可由下式表達:

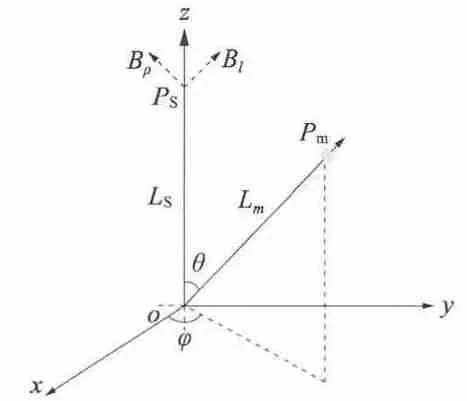
圖1 闡述永磁體位置的坐標系

位于永磁體所在轉軸上的P 點在xyz 坐標系的坐標P(x，y，z)可用式(3)表述。

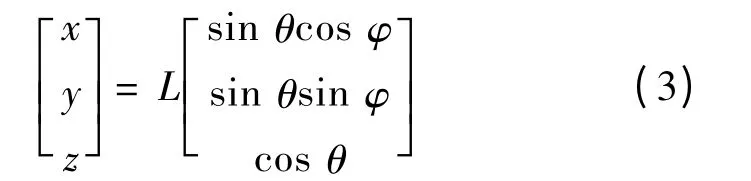
式中:L 為P 點到原點的距離。顯然，P 點坐標P(x，y，z)由θ，φ 唯一決定。

式(1)和式(2)提供了求解角度φ 的方法。在PS點放置三維磁感應強度傳感器S，測得磁感應強度Bx，By，Bz。則φ 可由下式求得:

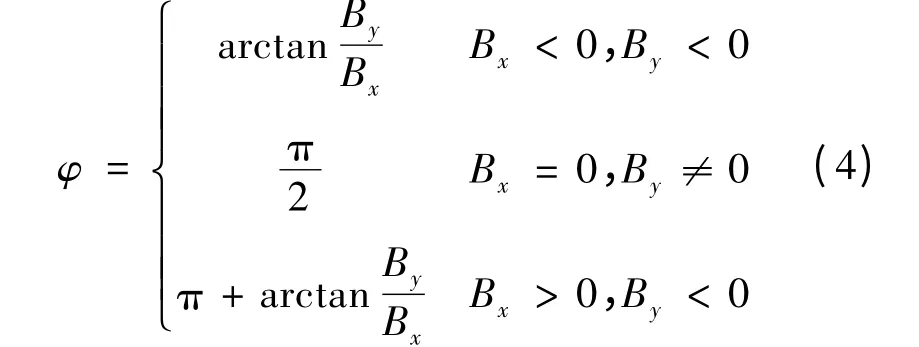
當Ls取恰當值時，B 值與θ 成單值函數關系，即B=f(θ)為單調函數，θ∈［0，θ0］。當S 測得點磁感應強度為B^時，確定Bk+1＜B^＜Bk(k∈［1，n -1］)。則此時轉軸與z 軸的夾角θ^可由下式求得:

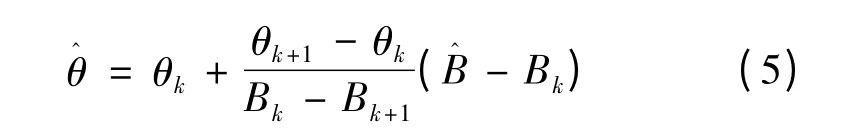
式中:θk∈［0，θ0］，Bk=f(θk)(k =1，2，…，n -1)。θ^的精度取決于n 的大小和Bk的精確度。

根據式(4)和式(5)，求得θ 和φ，確定球形電動機轉子位置。據此，下文構思設計了球形電動機的位置檢測系統。

1.1 球形電動機位置檢測系統設計

圖2 為是本文研究的球形電動機實體模型，詳細參數如表1 所示。圖3 和圖4 展示了檢測系統的設計理念，三維磁感應強度傳感器分別置于x1y1z1，x2y2z2，x3y3z3坐標系中的z1，z2，z3軸上。檢測點到原點O 的距離為Ls。x1y1z1坐標系由XYZ 坐標系逆時針繞X 軸旋轉α 角得到;XYZ 坐標系繞Z 軸逆時針旋轉120°后再繞x 軸逆時針旋轉α 角得到x2y2z2坐標系;x3y3z3坐標系由XYZ 坐標系繞Z 軸逆時針旋轉240°后再繞x 軸逆時針旋轉α 角得到。

圖2 球形電動機實體模型

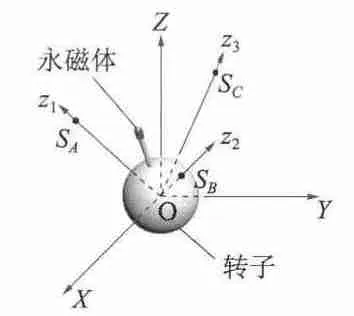
圖3 檢測系統立體示意圖

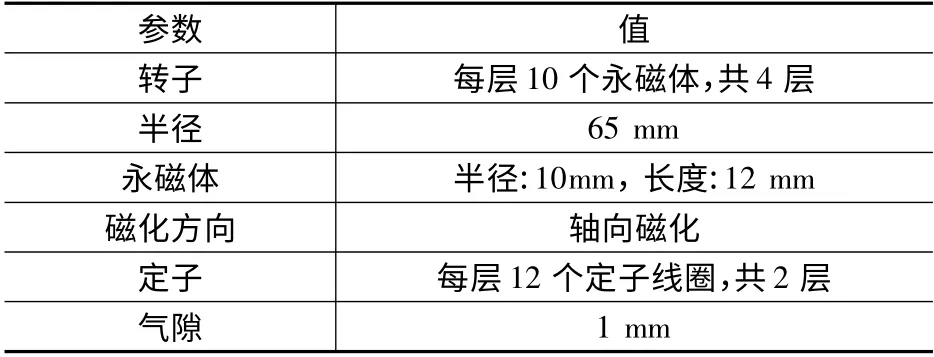
表1 永磁球形電動機參數

將檢測區域劃分為圖4 中A，B，C 三塊區域。轉軸運動至A 區域時，由SA負責檢測轉軸上P 點位于x1y1z1坐標系中的位置P(x1，y1，z1)。通過坐標轉移變換可得到P 點在絕對參考坐標系XYZ 中的坐標。式(6)給出了P(X，Y，Z)的求解方法。

式中:L 為轉軸上P 點到原點O 的距離;θ1和φ1分別為球形電動機轉軸與z1軸的夾角和轉軸在x1y1z1平面內的投影與x1軸的夾角。

同理，轉軸運動至區域B 時點P 在XYZ 坐標系內的坐標可由下式求得:

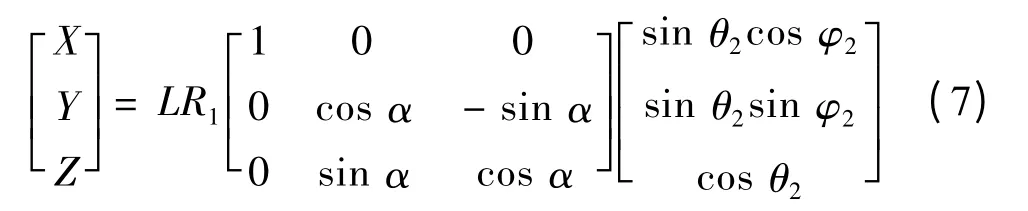
轉軸運動至區域C 時P 點在XYZ 坐標系內的坐標由式(8)求得。θ3和φ3分別為球形電動機轉軸與z3軸的夾角和轉軸在x3y3z3平面內的投影與x3軸的夾角。

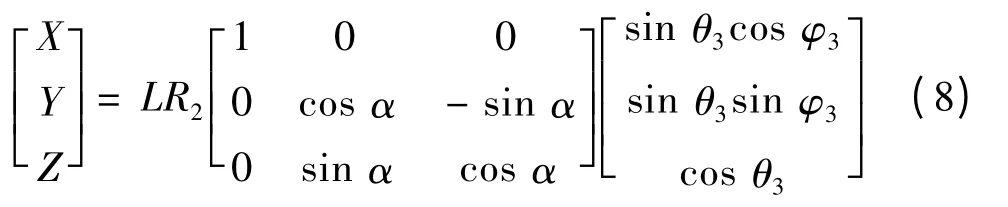
1.2 圓柱永磁體產生的磁感應強度計算

預知PS點的磁感應強度B 是前文提出算法實現的前提，而且掌握了解PS點磁感應強度Bx和By的變化范圍對角θ0的大小及三維磁感應強度傳感器的選擇至關重要。點的磁感應強度可以通過分布式磁偶極子法按照式(9)～式(12)求得［18］。

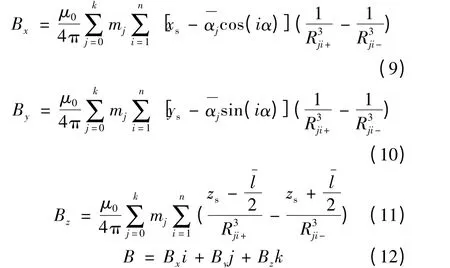
上述公式中，μ0是真空磁導率，k 和n 分別為分布式磁偶極法模擬的永磁體的圓周對數目以及每對圓周上含有的磁偶極子對數目，mj是位于第j 個圓周上的磁偶極子的磁偶極矩。γ 角為相鄰的兩個磁偶極子對應的圓心角。為第j 個圓周的半徑，且

1.3 檢測點磁感應強度計算分析

永磁體運動在A 區域內SA檢測的磁感應強度變化情況與永磁體運動在B、C 區域SB、SC感知的磁感應強度變化情況完全一樣。因此可僅分析運動于區域A 內SA檢測的磁感應強度變化情況。

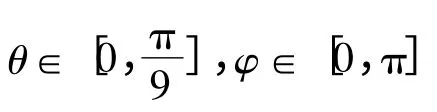
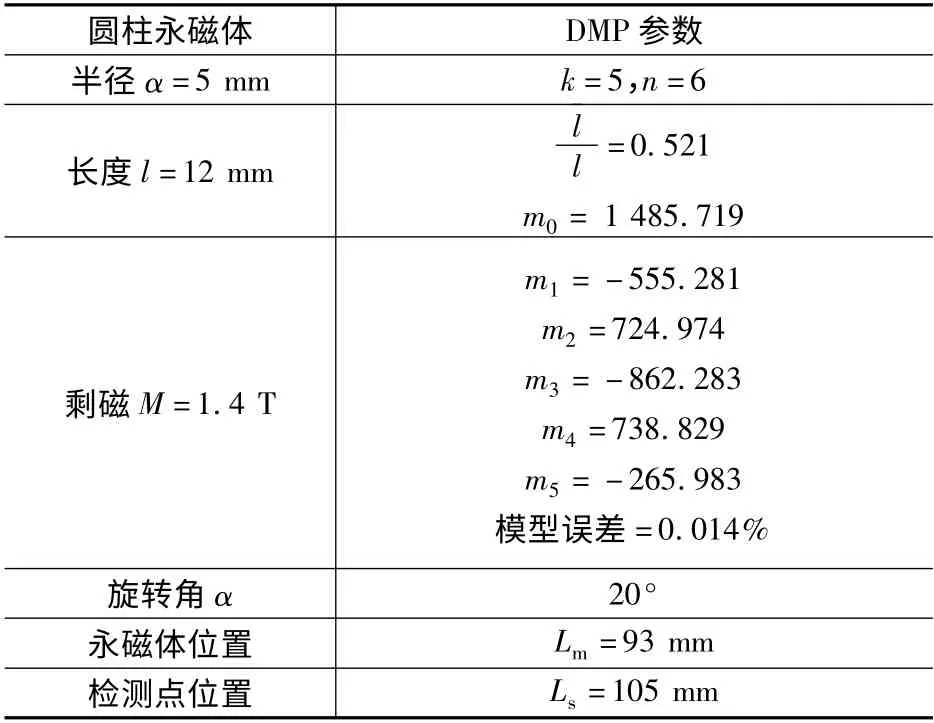
表2 磁源及固定檢測點參數

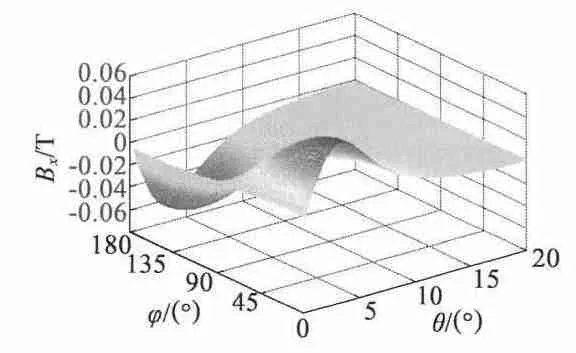
圖5 x 方向磁感應強度

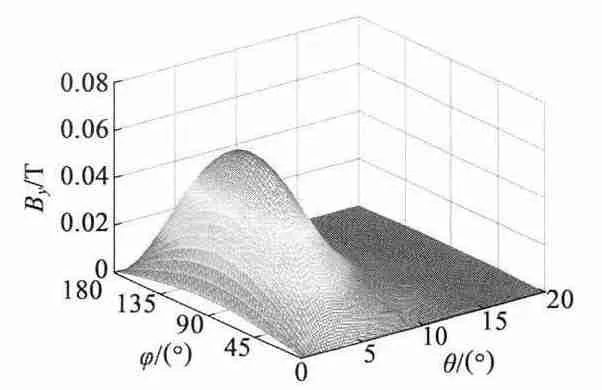
圖6 y 方向磁感應強度

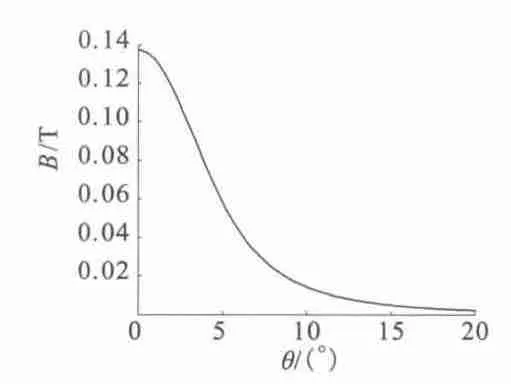
圖7 隨θ 變化的磁感應強度B

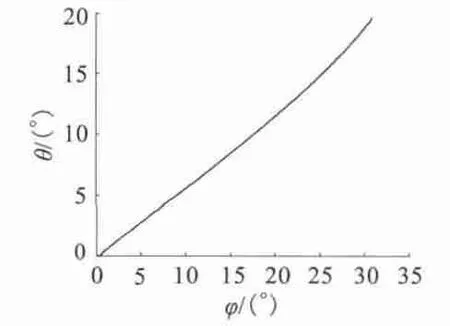
圖8 φ1 與θ1 的函數關系

1.4 轉子永磁體以及通電線圈對檢測點磁感應強度影響分析

轉子永磁體以及通電線圈對檢測點的磁感應強度影響會降低位置檢測的精度。因此，選擇檢測點位置時應以盡量減少轉子永磁體和通電線圈對檢測點磁感應強度影響為原則。圖9 是用MagNet 建立的本文研究的球形電動機模型，基于此模型分析轉子永磁體以及通電線圈對本文選取的檢測點磁感應強度影響。

圖9 球形電動機仿真模型

轉軸與Z 軸重合時記α 角為0°，轉子繞X 軸逆時針旋轉記為正，反之為負。圖10 刻畫了α 角變化范圍為［-20°，20°］時，固定檢測點A 的由轉子永磁體產生的磁感應強度變化情況。由于將整個檢測區域等分為三個部分，所以當轉子順時針旋轉時，雖檢測點A 受到的來自轉子永磁體的磁感應強度影響較大，但此時檢測點B 或C 檢測到的磁源永磁體產生的磁感應強度大于前者，轉子的位置檢測通過B 或C獲得。轉子逆時針旋轉時，從圖中可以看出，轉子永磁體對檢測點的磁場影響在5 ×10-4T 以下，而此時磁源永磁體作用于檢測點A 的磁感應強度較大，轉子永磁體對檢測結果的準確度有微弱的影響。

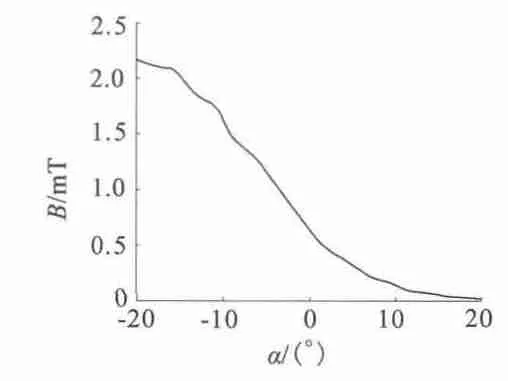
圖10 轉子永磁體產生的磁感應強度

圖11 分析的是一個通以電流1 A，1 200 匝的線圈，在檢測點所在圓周產生的磁感應強度。從圖中可以看出，通電線圈在圓周上產生的磁感應強度在1 ×10-4T 左右，對檢測點的影響可以忽略。由于定子線圈與檢測點是相對靜止的，將檢測點選擇在過兩個定子線圈中間線的平面與圓周的交點處可以最大限度降低通電線圈對檢測點磁感應強度的影響。

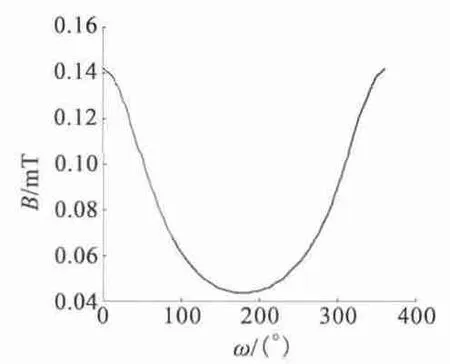
圖11 通電線圈產生的磁感應強度

2 仿真分析

本文選取了轉軸運動在A 區域內的不同位置的P 點的一系列坐標P(Xi，Yi，Zi)(L 取100 mm)，通過MagNet 軟件，求解出PS點在轉軸上P 點處于這些位置時的磁感應強度Bxi、Byi以及Bi。再通過公式求解出相應的點P 的坐標P(，，)。圖12和圖13 展示了三維和二維的定位結果。圖14 展示了P 在不同位置時的定位誤差。仿真結果表明，轉軸運動在A 區域內時，定位誤差在2 mm 以內。另外，前20 個采樣點的定位誤差比剩余采樣點的小，這是由于前者這些點對應的轉軸與z1軸的夾角θ較后者小;前者采樣點對應的檢測點磁感應強度較強，計算結果精確度高。提高θ 角較大時的定位精度以及擴大檢測區間范圍，取決三維磁感應強度傳感器測量下限的提高。

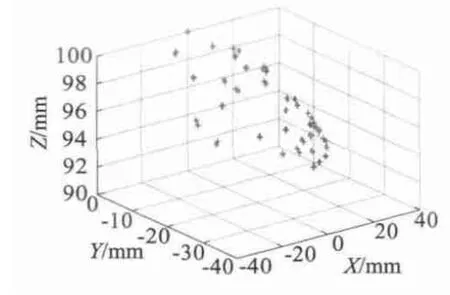
圖12 三維空間位置

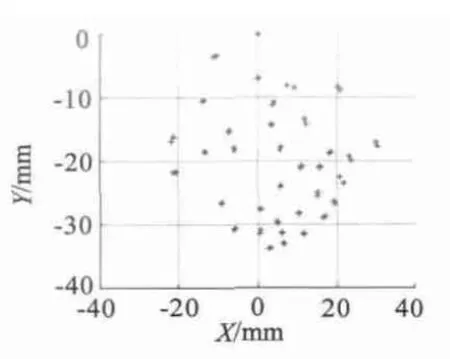
圖13 二維空間位置

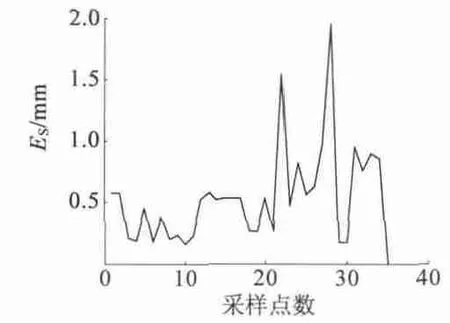
圖14 位置誤差

3 結 語

本文用分布式磁偶極子法分析了磁源永磁體隨轉軸在檢測區域轉動時空間固定點的磁感應強度變化情況。以此為基礎，通過固定檢測點的三個正交方向的磁感應強度數據的處理計算，獲得轉軸位于相對坐標系中的方位信息，再通過坐標轉移變換，得到球形電動機轉軸位于絕對坐標系中的位置。仿真結果表明了該方法的可行性。本文提出的非接觸式檢測方法能夠實現實時二自由度位置檢測，為以后進一步研究基于磁場的三自由度位置檢測提供了參考。

［1］ LEE K M，VACHTSEVANOS G，KWAN C. Development of a spherical stepper wrist motor［J］.Journal of Intelligent and Robotic Systems，1988，1(3):225 -242.

［2］ WANG J，JEWELL G W，HOWE D. A novel spherical actuator:design and control［J］.IEEE Transactions on Magnetics，1997，33(5):4209 -4211.

［3］ WANG J，JEWELL G W，HOWE D.Modelling of a novel spherical permanent magnet actuator［C］//Proceedings of IEEE International Conference on Robotics and Automation.1997:1190 -1195.

［4］ WEEK E M，REIARTZ T，HENNERBERGER G，et al.Design of a spherical motor with three degrees of freedom［J］.CIRP Annals-Manufacturing Technology，2000，49(1):289 -294.

［5］ KAHLEN K，VOSS I，PRIEBE C，et al.Torque control of a spherical machine with variable pole pitch［J］. IEEE Transactions on Power Electronics，2004，19(6):1628 -1634.

［6］ 蘇仲飛，劉昌旭，韋平順，等.機器人關節用三自由度球形直流伺服電機［J］.高技術通訊，1994(8):16 -18.

［7］ 黃聲華，陶醒世，林金銘. 三維電動機的電磁模型［J］. 電工技術學報，1994，9(4):17 -20.

［8］ 黃聲華，陶醒世，林金銘. 三維電動機力學模型及解耦控制［J］. 電工技術學報，1996，11(1):12 -16.

［9］ 程樹康，崔淑梅，劉寶廷，等.正交圓柱結構雙氣隙共磁鋼三自由度電動機初探［J］.中國電機工程學報，1997，17(5):7 -11.

［10］ 崔淑梅，柴風，程樹康.正交圓柱結構三維電動機磁系統分析［J］.微特電機，1999，27(6):26 -28.

［11］ LI H，XIA C，SHI T.Spherical harmonic analysis of a novel Halbach array PM spherical motor［C］//IEEE International Conference on Robotics and Biomimetics.2007:2085 -2089.

［12］ LI H，XIA C，SHI T.3 -D magnetic field and torque analysis of a novel Halbach array permanent - magnet spherical motor［J］.IEEE Transactions on Magnetics，2008，44(8):2016 -2020.

［13］ XIA C，SONG P，LI H，et al. Research on torque calculation method of permanent-magnet spherical motor based on the finite-element method［J］. IEEE Transactions on Magnetics，2009，45(4):2015 -2022.

［14］ LEE K M，KWAN C K.Design concept developpment of a spherical stepper for robotic applications［J］.IEEE Transactions on Robotics and Automation，1991，7(1):175 -181.

［15］ STEIN D，CHIRIKJIAN G S.Experiments in the commutation and motion planning of a spherical stepper motor［C］//ASME Design Engineering Technical Conferences and Computers and Information in Engineering Conference.2000:1 -7.

［16］ STEIN D，SCHEINERMAN E R，CHIRIKJIAN G S.Mathematical models of binary spherecal - motion encoders［J］. IEEE/ASME Transactions on Mechatronics，2003，8(2):234 -244.

［17］ 王群京，錢喆，李爭，等. 基于機器視覺的永磁球形步進電動機轉子位置檢測方法［J］.中國電機工程學報，2008，28(36):73 -79.

［18］ SON H，LEE K M. Distributed multipole models for design and control of PM actuators and sensors［J］. IEEE/ASME Transactions on Mechatronics，2008，13(2):228 -238.