4點彎曲載荷作用下殘余應力與彈性模量比對涂層/基體材料界面能量釋放率的影響

楊班權，董 釗，陳學軍，孫煒海

(1．裝甲兵工程學院機械工程系，北京100072;2．北京科技大學數理學院應用力學系，北京100083)

基體表面的涂層(薄膜)材料發揮著重要的作用，如耐熱、耐高溫、耐腐蝕和耐磨損等［1］。工程應用中的多數涂層/基體材料，其涂層的壽命很大程度上決定了整個零部件或設備的壽命;而涂層/基體材料的典型失效模式是涂層與基體的界面開裂(或脫層)［2-3］，因此，涂層與基體的界面開裂行為研究具有重要的理論價值與實踐意義。

若不考慮導致涂層與基體材料界面開裂的外界因素，如載荷條件和環境因素(高溫、腐蝕、疲勞、摩擦磨損等)，抵抗涂層與基體間界面開裂的關鍵本征參數(或內因)是涂層與基體間的界面結合性能［2-3］，而涂層/基體材料的界面斷裂行為分析是研究涂層/基體界面結合性能的基礎。涂層與基體材料的界面結合性能研究中，4點彎曲方法仍然是目前最常用的方法之一［2］。關于涂層/基體材料的界面斷裂行為研究目前已取得了不少成果［4-7］，但是這些研究成果多數情況下都沒有考慮殘余應力對界面斷裂行為的影響。

由于在涂層材料的制備、前后熱處理工藝或服役過程中，涂層與基體材料之間存在的晶格失配或熱膨脹系數差異等問題導致界面不穩定，其表現形式為由于溫度變化或外界載荷的作用導致涂層與基體之間的應變失配，這種失配會引起涂層內高達幾十至幾百兆帕的殘余應力［8-10］，有時甚至會達到吉帕的量級［8-10］。這種量級的殘余應力會導致薄膜產生嚴重的彎曲變形以致脆斷失效，對涂層材料界面斷裂行為的影響也十分明顯［5］。

本文在考慮殘余應力作用效應的基礎上，采用ANSYS有限元計算方法，研究了在4點彎曲載荷作用下，殘余應力與彈性模量比對涂層/基體材料界面能量釋放率(裂紋擴展驅動力)及其相角的影響。

1 有限元力學建模及計算過程

在殘余應力與4點彎曲載荷作用下，涂層與基體的界面斷裂行為的力學模型如圖1所示。

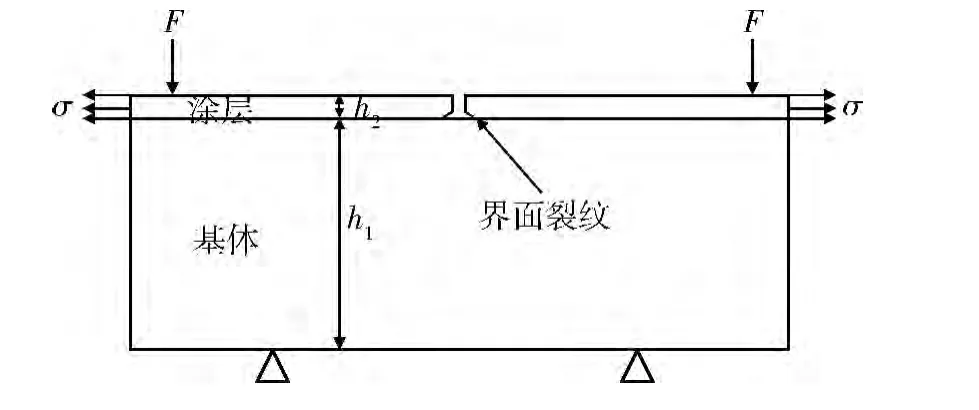
圖1 殘余應力與4點彎曲載荷作用下涂層/基體材料的界面斷裂行為示意圖

圖1中:F為4點彎曲載荷;σ為殘余拉應力，施加在涂層的橫截面;h1為基體的厚度;h2為涂層的厚度。根據線彈性斷裂力學理論，平面應變下的裂紋尖端能量釋放率的計算公式為［11］

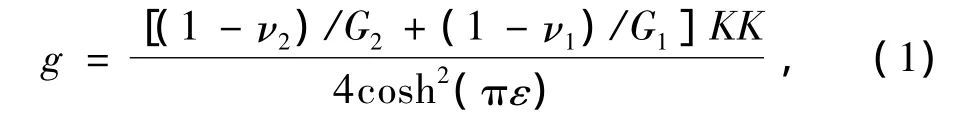
式中:ν1、ν2分別為基體和涂層的泊松比;G1、G2分別為基體和涂層的剪切模量;ε為參數，

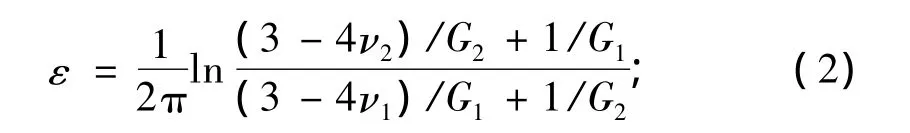
式(3)中，ψ為相角(與材料界面結合性能有關的參數)，

ω=φ-εln r，為幅角，φ為用復數表示的位移幅角，r為節點到裂紋尖端的距離，β=arctan(2ε)，為角度，

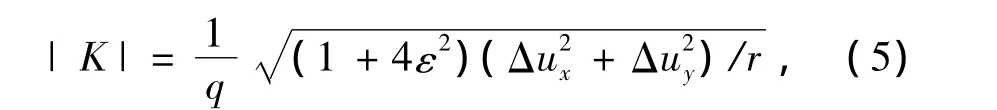
其中

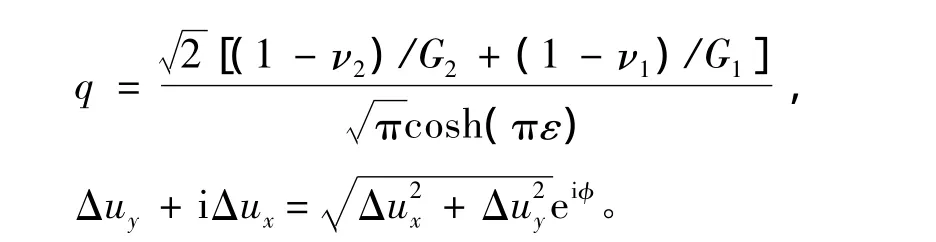
建模過程中，選取電鍍鉻涂層/鋼基體材料為研究對象。電鍍鉻涂層廣泛應用于槍、炮身管的內壁中，具有耐熱、耐磨損和耐腐蝕的特點。這里，鉻涂層的厚度 h2=150μm，涂層的彈性模量為 E2=280 GPa，ν2=0．22;基體的彈性模量為E1=210 GPa，ν1=0．28，厚度 h1=2 mm;殘余應力 σ =250 MPa。

在有限元建模計算過程中，采用PLANE182單元。根據圖1的力學模型，采用ANSYS建立有限元計算模型，如圖2所示。

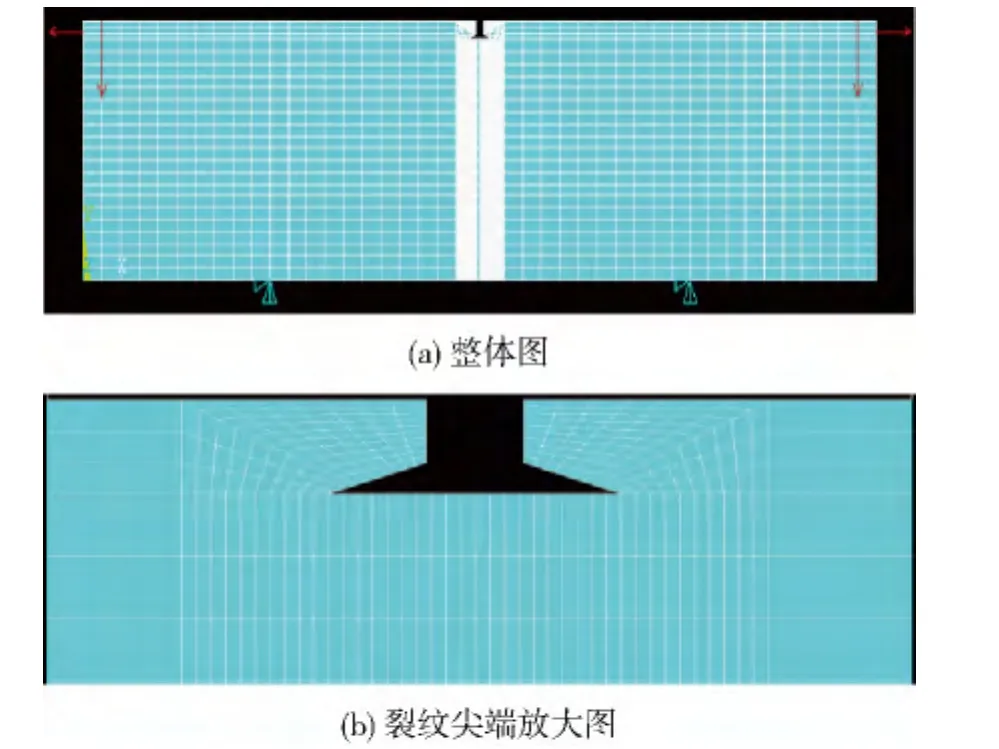
圖2 有限元計算模型

2 計算結果及其分析

應用ANSYS10．0建模分析，首先得出裂紋尖端附近節點位移;然后計算裂紋尖端的能量釋放率。計算過程中，分析了網格劃分密度對計算結果的影響，劃分的網格密度有足夠的精度以保證計算結果的正確性。加載后的變形、應力云圖如圖3所示。

圖3 加載后的變形、應力云圖

由圖3可見:在對稱載荷作用下，結構變形、應力分布表現出對稱特征，在裂紋的尖端附近出現了明顯的應力集中現象。由于結構變形及應力分布特征的對稱性，選取裂紋尖端的一半為例進行研究。

依次改變涂層厚度、彈性模量、殘余應力的大小，分別建立不同彈性模量比E2/E1、不同殘余應力的ANSYS模型，記錄每次計算的節點位移和應力，研究殘余應力與彈性模量比對涂層/基體材料界面能量釋放率及其相角的影響，如圖4-7所示。

由圖4可見:殘余應力對能量釋放率的影響十分明顯，隨著殘余拉應力的增大，能量釋放率將增大，因此殘余拉應力將促使裂紋擴展;反之，可通過減小殘余壓應力來降低能量釋放率，抑制裂紋的擴展。

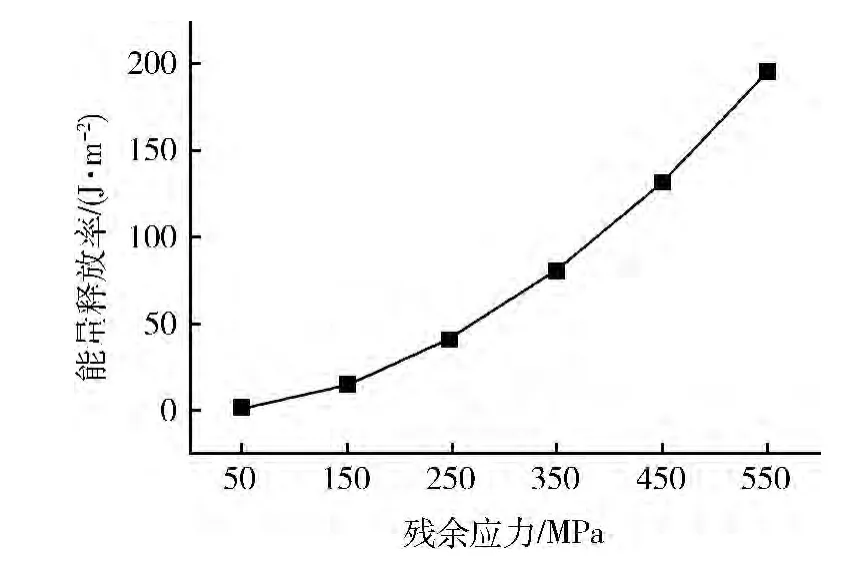
圖4 殘余應力對能量釋放率的影響

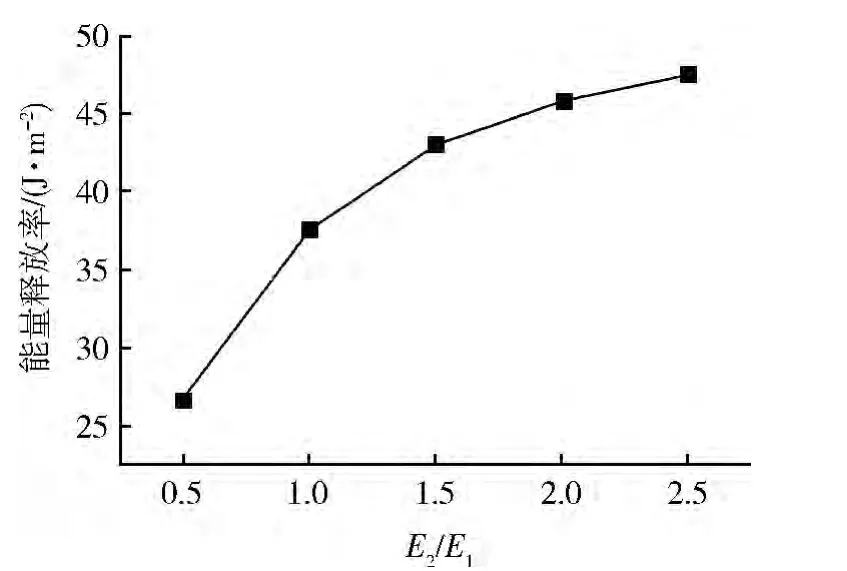
圖5 彈性模量比對能量釋放率的影響

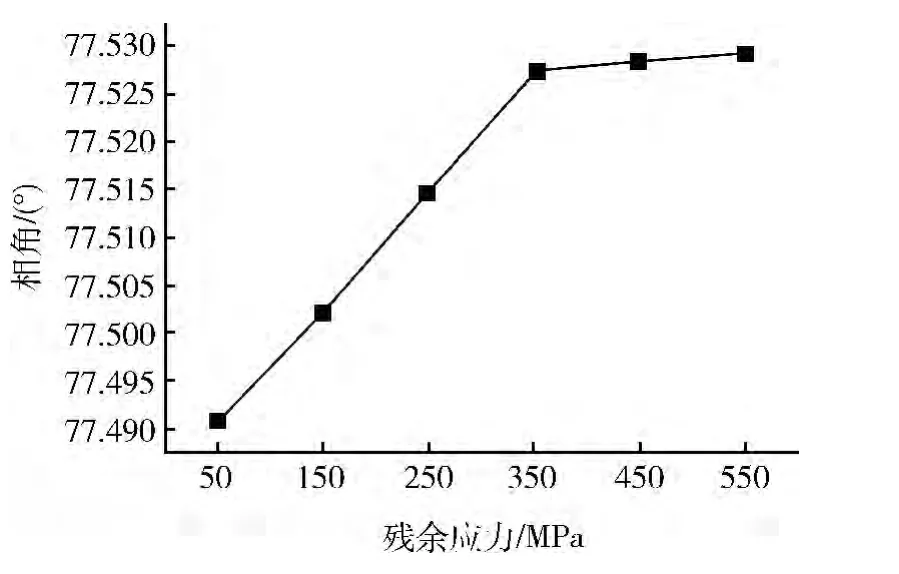
圖6 殘余應力對相角的影響

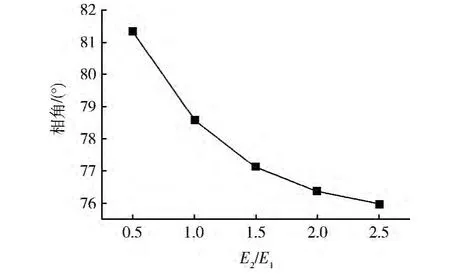
圖7 彈性模量比對相角的影響

由圖5可見:彈性模量比對能量釋放率也有影響，能量釋放率隨著彈性模量比的增大而增大。

由圖6可見:能量釋放率中的相角隨著殘余拉應力的增大而增大，但是影響不是十分顯著。

由圖7可見:能量釋放率中的相角隨彈性模量比的增大而減小，但與殘余應力對相角的影響程度相比，彈性模量比對相角的影響比較顯著。

3 結論

本文在考慮殘余應力效應的基礎上，研究了4點彎曲載荷作用下殘余應力和彈性模量比對涂層/基體材料界面能量釋放率及其相角的影響。本文的計算結果適用于厚涂層/基體材料體系，且假定殘余應力沿著橫截面均勻分布。下一步將對微/納米尺度下，考慮梯度殘余應力效應的單層膜/基體材料或多層膜結構材料的界面斷裂行為與界面結合性能進行深入研究。

［1］ Freund L B，Suresh S．Thin Film Materials，Stress，Defect Formation and Surface Evolution［M］．Cambridge:Cambridge University Press，2003:1-6．

［2］ Volinsky A A，Moody N R，Gerberich W W．Interfacial Toughness Measurements for Thin Films on Substrates［J］．Acta Materialia，2002，50(3):441-466．

［3］ Chou T L，Yang SY，Wu CJ，et al．Measurement and Simulation of Interfacial Adhesion Strength Between SiO2Thin Film and III-V Material［J］．Microelectronics Reliability，2011，51(9/11):1757-1761．

［4］ Lin M J，Chen R S．Effect of Gradient Residual Stress on Adhesion for a Center-anchored Circular Plate and Its Underlying Substrate［J］．Sensors and Actuators A，2004，115:109-117．

［5］ Matin M A，Ozaki K，Akai D，et al．Correlation Between Residual Stresses and Bending in Functional Electroceramic-based MEMS Actuator［J］．Computational Materials Science，2014，85:253-258．

［6］ Fu Y Q，Du H J，Sun C Q．Interfacial Structure，Residual Stress and Adhesion of Diamond Coatings Deposited on Titanium［J］．Thin Solid Films，2003，424(1):107-114．

［7］ Nie P L，Shen Y，Chen Q L，et al．Effects of Residual Stresses on Interfacial Adhesion Measurement［J］．Mechanics of Materials，2009，41(5):545-552．

［8］ Zheng X J，Li JY，Zhou Y C．X-ray Diffraction Measurement of Residual Stress in PZT Thin Films Prepared by Pulsed Laser Deposition［J］．Acta Materialia，2004，52:3313-3322．

［9］ Ohno T，Fu D，Suzuki H，et al．Residual Stress in Lead Titanate Thin Film on Different Substrates［J］．Journal of the European Ceramic Society，2004，24:1669-1672．

［10］ Benegra M，Lamas D G，Fernández M E．et al．Residual Stresses in Titanium Nitride Thin Films Deposited by Direct Current and Pulsed Direct Current Unbalanced Magnetron Sputtering［J］．Thin Solid Films，2006，494:146-150．

［11］ Hutchinson J W，Suo Z．Mixed Mode Cracking in Layered Materials［J］．Advances in Applied Mechanics-transactions of the ASME，1992，29:63-191．