重型柴油機空氣濾清器技術狀況監測方法

趙永東，趙文柱，王憲成，和 穆

(裝甲兵工程學院機械工程系，北京100072)

空氣濾清器的主要作用是濾清進入氣缸的空氣，除去空氣中所攜帶的塵土等雜質，減輕發動機內各零件之間的磨損。隨著空氣濾清器內塵土的增加，進氣阻力會增大，甚至發生空氣濾清器擊穿，將嚴重影響發動機正常工作。因此，必須定期對空氣濾清器進行保養。目前，對某重型柴油機空氣濾清器技術狀況的檢測僅通過阻力指示器的報警實現。測試時，原位穩定發動機轉速2 000 r/min，當空氣濾清器進氣阻力達到(8±0．6)kPa時，信號燈亮，指示器報警。但是該方法只適用于原位測試，在車輛行駛過程中無法有效地監測空氣濾清器的技術狀況。根據某地實際調研情況可知:大多數空氣濾清器擊穿都是由于不能實時監測其使用情況，在行駛過程中發生的。

在車輛行駛過程中對空氣濾清器進行監測可以實時了解其技術狀況，防止因無法預知空氣濾清器擊穿而造成的嚴重事故。為此，筆者通過分析空氣濾清器內部氣體流動過程，選用經驗公式計算各部件壓降損失，推導出了空氣濾清器的技術狀況監測數學模型。通過臺架和實車試驗，驗證了該模型能夠準確地反映空氣濾清器的使用情況，可實時監測空氣濾清器的技術狀況，為其及時保養提供依據。

1 空氣濾清器監測模型建立

1．1 氣體流動過程假設

空氣濾清器內部流動為氣固兩相流動，但是分析和計算兩相流動問題比較復雜，為了方便計算，將空氣濾清器內部流動簡化為空氣的單相流動，對內部氣體作如下假設［1-3］:1)空氣中塵土對空氣流動的影響忽略不計，空氣運動不受塵土的影響;2)空氣流動過程為定常流動;3)忽略溫度的影響，認為整個流動過程為等溫過程;4)二級濾清器(金屬濾網)采用多孔介質模型，在流動過程中金屬濾網完全固定，空氣濾清器內部構件為絕對剛體。

1．2 等效流通截面積模型公式推導

某重型柴油機空氣濾清器主要由一級濾清器(旋風筒)、二級濾清器(濾塵絲盒)、蓋板、頭部等部分組成，其結構簡化模型圖1所示。

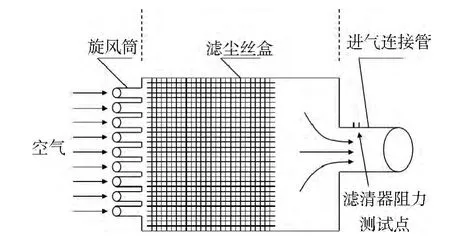
圖1 空氣濾清器結構簡化模型

忽略空氣濾清器進氣口至旋風筒的損失，即整個空氣濾清器的壓降ΔP由旋風筒壓降ΔP1、濾網壓降ΔP2和進氣連接管處局部阻力損失ΔP3組成:

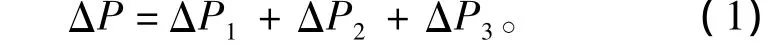
1．2．1 旋風筒壓降計算模型

軸向旋風筒主要由中心管、旋流葉片、導流管組成。在旋流葉片的導流作用下，空氣沿葉片高速旋轉運動，在超出導流管端口時改變方向，中心導流管急速逆向流動。在離心力和慣性力的作用下，大顆粒的塵土被收集到集塵箱，較清潔的空氣進入二級濾清器。

旋風筒的壓力損失主要包括旋風筒形狀壓力損失、氣體流動摩擦損失和內部漩渦耗散損失［4-5］。在旋風筒壓降計算方面，國外學者做了大量的研究，根

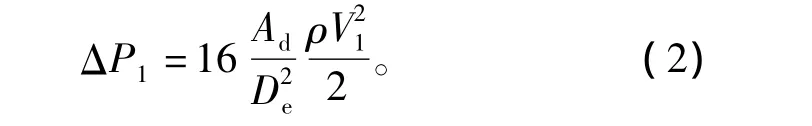
式中:Ad為旋風筒進氣口面積(m2);De為旋風筒出氣口直徑(m);ρ為氣體密度(kg/m3);V1為進氣口氣流平均流速(m/s)。

1．2．2 金屬濾網壓降計算模型

金屬濾網由24層粗濾網和20層細濾網疊加而成，網孔尺度一般是絲網直徑的幾十倍。為了計算壓降，必須簡化模型。在實際計算中，將金屬濾網區域等效為多孔介質模型，根據Darcy-Stoke方程［7］，可得據試驗數據和實踐經驗提出了適用于旋風筒壓降的經驗公式，本文采用Lapple建立的計算式［6］:

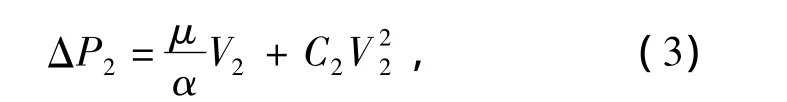
其中

式中:1/α為黏性阻力系數;C2為慣性阻力系數;μ為氣體動力黏度(Pa·s);V2為通過濾芯的氣流流速(m/s);DP為濾芯孔隙平均直徑(m);ε為濾芯孔隙率。其中，DP可以從材質報告中得到，ε指材料內空孔的體積與總體積之比。對于油浴式空氣濾清器，一般絲網直徑不大于0．30 mm，孔隙率不大于97%［8］。

1．2．3 進氣連接管處局部阻力損失

清潔空氣由空氣濾清器到進氣連接管時，流通面積突然縮小，流動狀態發生急劇變化，造成了能量的損失，根據工程流體力學知識，局部損失表示為［9］

其中

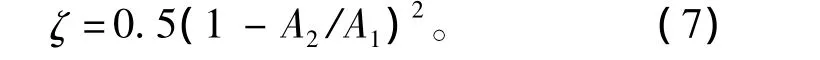
式中:ζ為局部阻力系數;V3為空氣濾清器出口處流速(m/s);g為重力加速度(m/s2);A1為空氣濾清器截面積(m2);A2為進氣連接管截面積(m2)。

1．2．4 空氣濾清器等效流通截面積數學模型

氣體質量流量為

氣體體積流量為

式中:A為氣體流通截面積(m2);V為氣體流速(m/s)。

根據質量守恒定律，聯立式(1)、(2)、(6)、

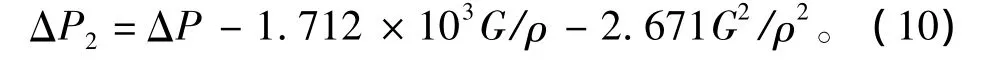
(8)，代入濾清器結構參數，可得將式(10)代入到式(3)中，聯立式(4)、(5)、(9)可得到空氣濾清器流通截面積:

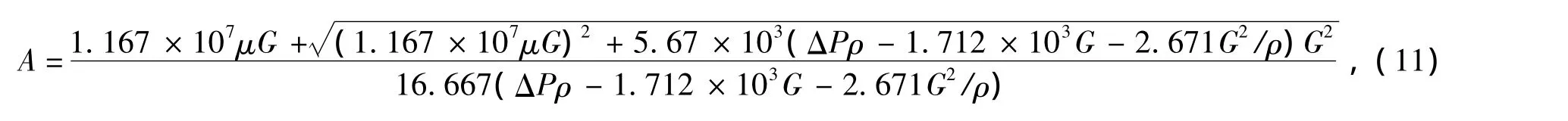
式中:Aφ為空氣濾清器等效流通截面積(m2);μφ=，為空氣濾清器流量系數。

氣體動力黏度根據經驗公式近似計算［9］:

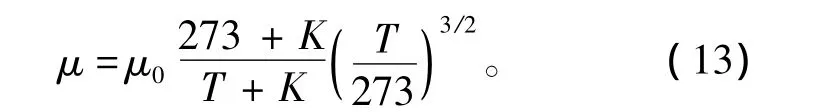
式中:μ0為氣體在0℃時的動力黏度(空氣為1．71×10-3Pa·s);T為氣體熱力學溫度(K);K為依氣體種類而定的系數(空氣為111)。

氣體密度計算公式:

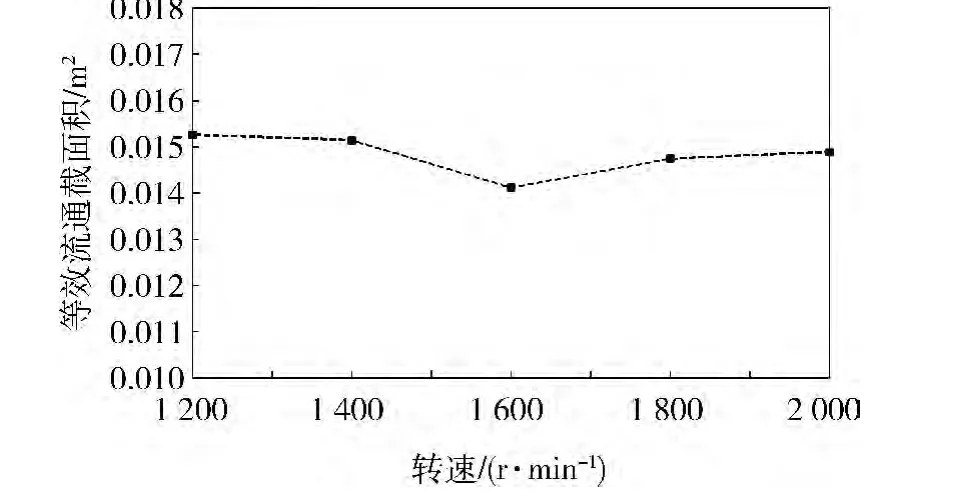
圖2 不同轉速下等效流通截面積

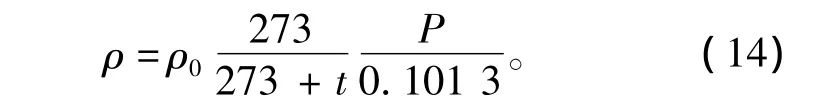
式中:P 為氣體壓強(MPa);ρ0=1．293 kg/m3，為標準大氣壓0℃時空氣密度;t為氣體溫度(℃)。

目前，該型柴油機空氣濾清器并沒有高原條件下進氣阻力閾值的規定，但是根據數學模型的定義，無論在高原地區還是平原地區，等效流通截面積的值是不變的。因此，根據某型柴油機《空氣濾清器使用維護說明書》的規范，平原地區標定工況下進氣流量達到最大值1．24 kg/s時，濾清器阻力最大值為 13．72 kPa，最小值為 3．63 kPa，由此，可以計算出該空氣濾清器等效流通截面積的極限值分別為0．008 9 m2和 0．031 6 m2。器的等效流通截面積，5組數據的標準差為4．49×10-4，誤差為4．82%，通過數值可以看出:不同轉速下的等效流通截面積變化不大，且都在極限值范圍之內。由此證明了推導出的空氣濾清器等效流通截面積模型穩定性較好，適用于高原地區。

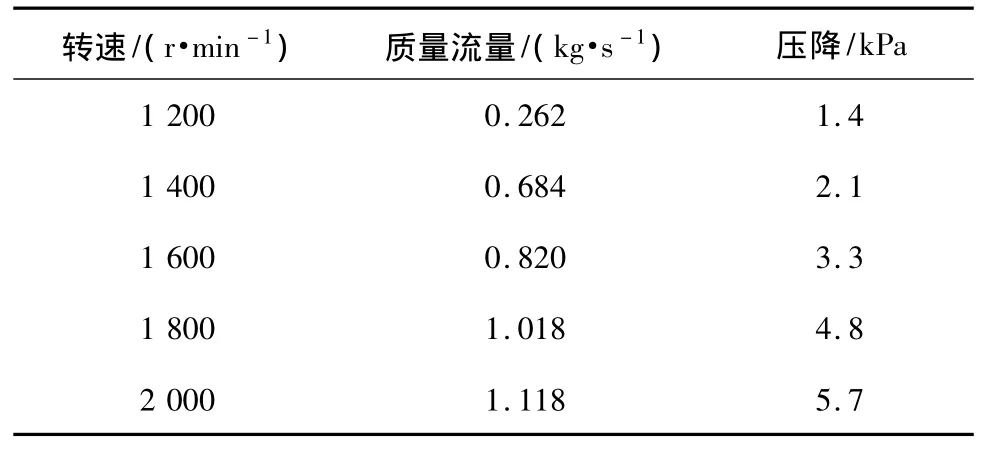
表1 臺架試驗測試數據

2 臺架試驗驗證

2．2 模型單調性驗證

空氣濾清器的等效流通截面積在實體上進行測量比較困難，難以得到其真實值。通過開展臺架試驗，對模型的穩定性和單調性進行檢驗，從而驗證模型的正確性。

2．1 模型穩定性驗證

試驗在車輛動力性能實驗室進行，環境條件:大氣壓力88．9 kPa;大氣溫度34℃。測取不同轉速下進入到發動機的空氣質量流量以及濾清器的壓降，通過式(12)計算濾清器的等效流通截面積，計算結果如圖2所示。表1為臺架試驗測試數據。

由圖1可見:空氣濾清器等效流通截面積不隨轉速升高而增大，不同工況下其數值變化不大。取5次不同工況下的平均值0．014 m2為該空氣濾清

在空氣濾清器試驗臺架上進行空氣濾清器容塵試驗，試驗選用國際標準(ISO)規定的標準試驗粉塵。試驗環境溫度20℃，大氣壓力86．65 kPa。試驗時調節進氣流量為1．24 kg/s，按照含塵濃度2 g/m3對被試驗的空氣濾清器進行均勻連續加灰塵10 min，然后記錄下進氣阻力，每10 min做一組記錄，直至進氣阻力達到13．72 kPa左右為止。圖3為進氣阻力隨時間變化的曲線，可以看出:隨著灰塵的不斷增加，進氣阻力不斷增大，由6．86 kPa增加到13．83 kPa。圖4為根據模型計算出的等效流通截面積隨時間變化的曲線，可以看出:空氣濾清器等效流通截面積隨時間單調下降，在440 min內由0．015 4 m2減小到 0．009 2 m2，減小了 0．006 2 m2，整個容塵試驗中等效流通截面積都在所計算的極限值范圍之內變化，進一步驗證了模型的正確性。

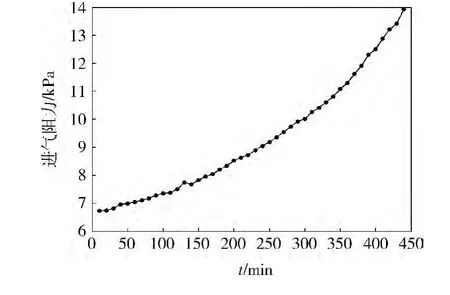
圖3 進氣阻力隨時間變化的曲線

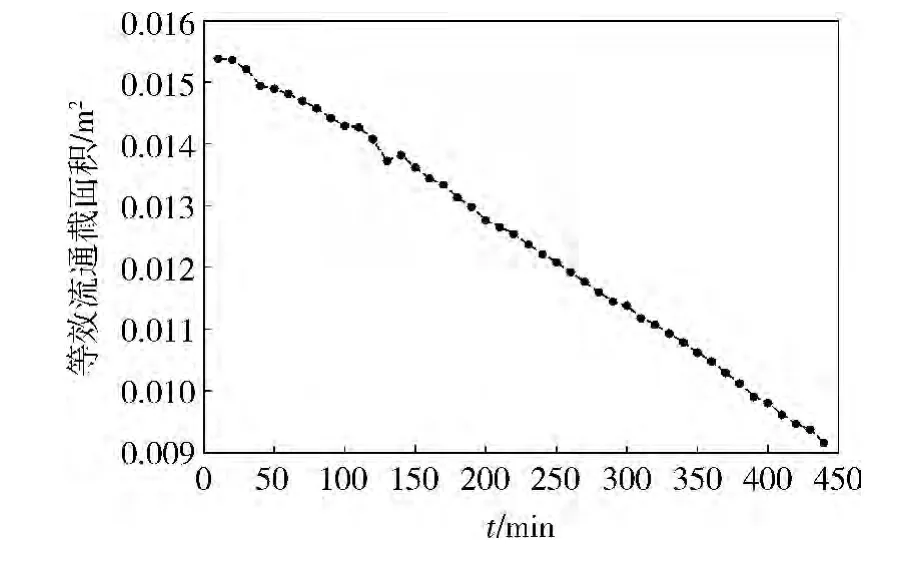
圖4 等效流通截面積隨時間變化的曲線

3 實車試驗

3．1 實車原位空轉試驗

在北京某地區對該型柴油機進行實車原位空轉試驗，環境溫度20℃，大氣壓力100 kPa。試驗時，穩定發動機轉速在 600～2 000 r/min，每升高200 r/min測試1次，分別測量大氣壓力、大氣溫度、濾清器后壓力、壓氣機前壓力、壓氣機前溫度等參數。進氣流量參照文獻［10］中的方法計算，得出每個工況點下的等效流通截面積如圖5所示，計算得出其平均值為0．012 8 m2，相對平均值最大波動為0．000 6 m2，誤差為 4．98%。

圖5 不同轉速下實車原位試驗等效流通截面積

3．2 實車跑車試驗

在新疆葉城某訓練場進行實車跑車試驗，場地含塵量為2．0 ～7．0 g/m3，環境溫度10 ℃，大氣壓力86．82 kPa。試驗使用同一臺車連續行駛3 h，每行駛1 h后進行原位測試。測試時，穩定轉速在600～2 000 r/min，每升高200 r/min測試1次。行駛不同時間后，原位空轉不同轉速下空氣濾清器壓降如圖6所示。從圖6中可知:原位空轉相同轉速下，行駛時間越長，空氣濾清器壓降越大。不同行駛時間后空氣濾清器等效流通截面積如圖7所示，對每次計算的不同轉速下的值取平均，得到3次等效流通截面積的平均值。隨著跑車時間的增長，空氣濾清器等效流通截面積單調減小，平均值由0．012 7 m2減小到 0．009 9 m2。

圖6 不同行駛時間后原位空轉空氣濾清器壓降

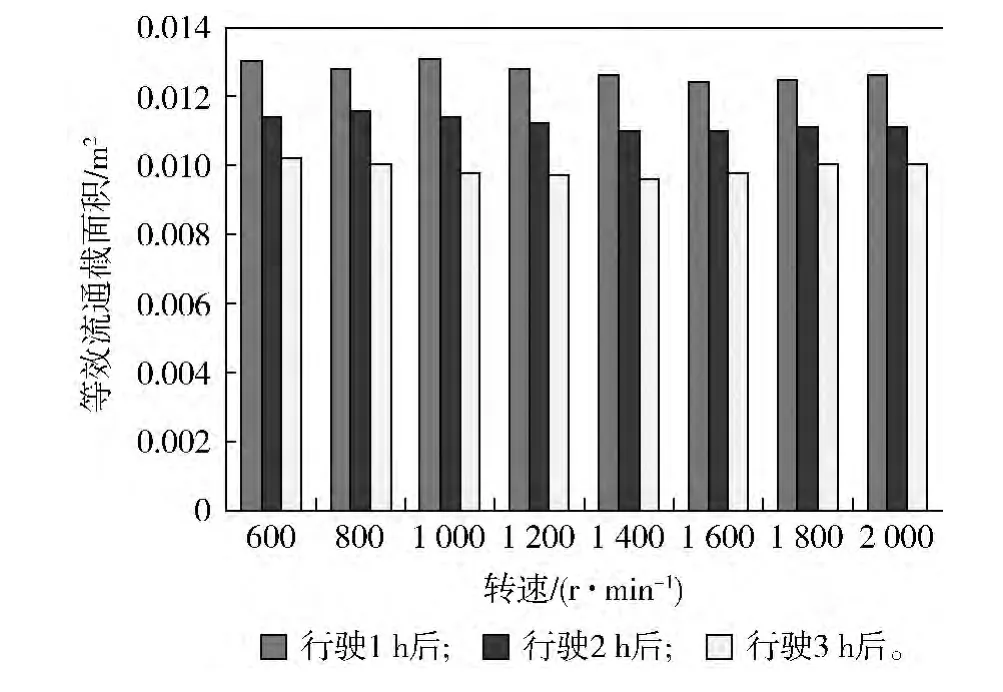
圖7 不同行駛時間后空氣濾清器等效流通截面積

在西藏某場地進行實車在線監測試驗，場地內有土嶺、溝壕等路障，路面浮土高度約20 cm，環境溫度28℃，大氣壓力59．6 kPa。試驗使用同一臺車連續行駛約40 min。行駛過程中進氣流量和進氣阻力隨時間的變化曲線分別如圖8、9所示，可以看出:由于行駛過程中工況、負荷的不同，進氣流量和進氣阻力呈現上下波動的情況，進氣流量最大值為0．58 kg/s，最小值為 0．43 kg/s，進氣阻力最大值為 1．845 kPa，最小值為1．020 kPa。根據推導出的空氣濾清器監測模型，求出等效流通截面積，其實測值與擬合值隨時間變化曲線對比如圖10所示。由于實際行駛中工況不穩定以及振動等其他因素的影響，等效流通截面積存在一定波動。由擬合曲線可知:隨著行駛時間的增長，等效流通截面積呈現不斷下降的趨勢，從0．017 m2減小到0．014 m2，約減少了0．003 m2。由此驗證了該模型實車監測的可行性和準確性。

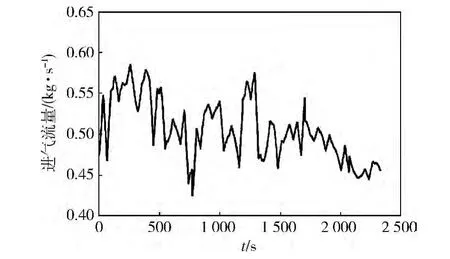
圖8 進氣流量隨時間的變化曲線

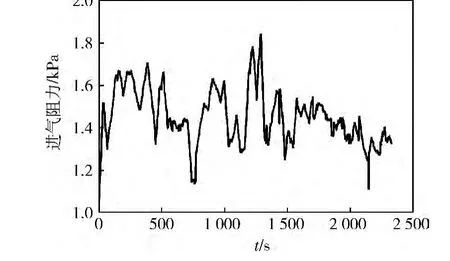
圖9 進氣阻力隨時間的變化曲線

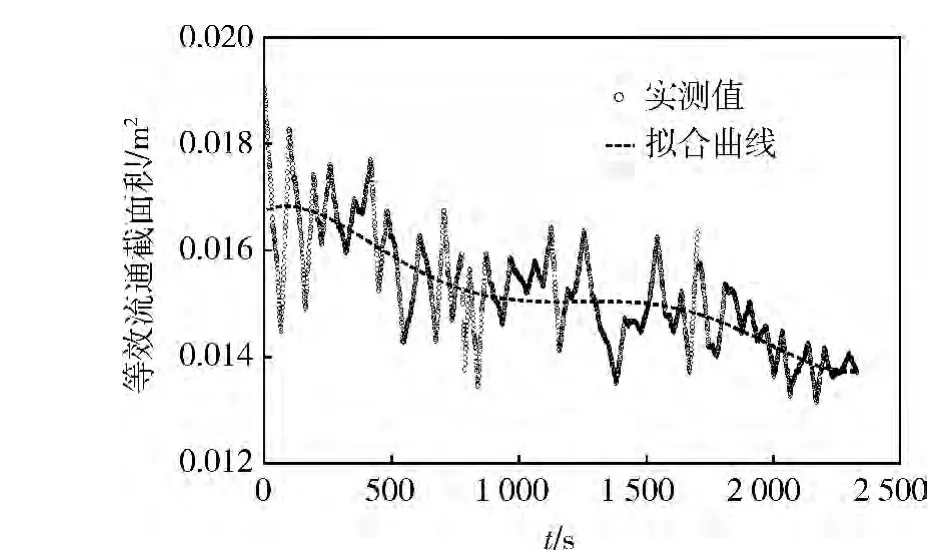
圖10 等效流通截面積實測值與擬合值隨時間的變化曲線對比

4 結論

本文通過簡化空氣濾清器物理模型，運用流體力學相關知識，參考經驗公式，建立了空氣濾清器等效流通截面積數學模型。通過臺架試驗驗證了該模型具有較好的穩定性、準確性以及單調性，能夠反映出空氣濾清器技術狀況的優劣程度。在不同海拔開展了實車試驗，結果表明:該模型同時適用于平原地區和高原地區，可以用于原位狀態監測，也可以用于實車在線監測。模型的運用對及時清洗空氣濾清器、合理安排保養周期具有重要意義，能夠有效預防因進氣阻力增大造成工作惡化以及因空氣濾清器擊穿造成磨損加劇等現象的發生。

［1］ 王偉，王仁人，張良．基于CFD的內燃機空氣濾清器內氣固兩相流數值模擬［J］．德州學院學報，2010，26(2):77-81．

［2］ 李佳，劉震濤，劉忠民，等．空氣濾清器流動過程仿真與試驗分析［J］．浙江大學學報，2012，46(2):327-332．

［3］ 張慧，富旭光．空氣濾清器的CFD分析及空氣流動性優化［J］．流動傳動與控制，2012，46(3):34-37．

［4］ 王德耕．旋風分離器速度分布指數及壓降計算通用模型［J］．化學工程，1998，26(1):44-48．

［5］ 吳克明，潘留明．旋風分離器壓力損失的數學模型及在設計中的應用［J］．化工環保，2005，25(2):156-160．

［6］ Shepperd C B，Lapple C E．Flow Patter and Pressure Drop in Cyclone Dust Collectors［J］．Ind End Chem，1939，31(8):972-984．

［7］ 李偉，王珂．基于CFD的濾材仿真參數研究［J］．研究與開發，2011(10):85-88．

［8］ 霍玉榮．空氣濾清器的設計與計算［J］．內燃機與配件，2011(7):9-12．

［9］ 歸柯庭，汪軍，王秋穎．工程流體力學［M］．北京:科學出版社，2003:15-16．

［10］ 和穆．高原坦克動力裝置狀態監測與壽命預測方法研究［D］．北京:裝甲兵工程學院，2012．