基于加權網絡模型的指揮節點重要度評估方法

姜志鵬，張多林，馬 婧，王 坤

(1．空軍工程大學防空反導學院，陜西西安710051;2．信息保障技術重點實驗室，北京100072;3．95876部隊，甘肅張掖734100)

指揮網絡作為作戰指揮體系建設的關鍵部分，其在攻防對抗中能否正常發揮作用將直接影響戰爭的勝負。節點在指揮網絡中的重要程度不盡相同，節點重要度評估研究有助于發現指揮網絡中的薄弱環節，對提高指揮網絡體系的可靠性和抗毀性具有重要參考價值［1］。

目前，網絡節點重要度評估方法很多，其核心思想主要是:“節點顯著性等價于重要性”，“節點刪除對網絡的破壞性等價于重要性”，“節點重要性不僅取決于自身，還與鄰接節點有關”等［2］。其評估方法主要有節點刪除法、節點收縮法、拓撲勢理論排序法、多屬性決策方法等［3-8］;提出的評估指標主要有節點度、臨近度、介數、隨機行走、凝聚度、接近度等［9-12］;評估范圍主要涉及全局、局部、社區重要性等［2，9］;網絡類型主要有靜態網絡、動態網絡、加權網絡［2，4-8］;評價對象主要涉及計算機網絡、犯罪關系網絡、病毒傳播網絡、謠言傳播網絡、社交網絡、科研合作網絡、電力網絡以及交通網絡等。

在軍事網絡節點重要度研究方面，賈子英等［1］將網絡化防空體系的節點重要度分為屬性重要度和結構重要度2個維度，并利用模糊偏序關系建立了屬性重要度評估模型;王欣等［12］針對指揮信息系統(Command Information System，CIS)的特點，考慮作戰任務需求和網絡拓撲結構對節點重要度的影響，提出了一種新的CIS節點重要度評估方法;李茂林等［13］在對作戰體系結構進行網絡描述的基礎上，分析了各個指標對節點重要度的影響，并根據網絡受損程度選出了最有效的重要性指標。上述方法都能夠在相關背景下進行節點重要度評估，對指揮網絡節點重要度評估具有很大的啟發和借鑒意義，但是這些研究都是基于無權網絡模型，且未考慮指揮網絡的社區特性，無法深度刻畫指揮網絡中各個節點之間的關系，不能真實地反映指揮網絡的特點。為此，本文考慮指揮網絡的任務需求和社區特點，提出了一種利用節點重要度評價矩陣確定加權網絡關鍵節點的方法，并從局部和全局2個方面研究了基于加權網絡模型的指揮節點重要度評估方法。

1 指揮網絡的加權網絡描述與特征分析

1．1 指揮網絡的加權網絡描述

無權網絡反映了節點間的基本連接方式和相互作用，但將實際系統抽象為這種簡單的拓撲結構往往會忽略許多客觀信息，導致問題描述不全面、不客觀，引入加權網絡可通過邊權值來刻畫節點間作用的強弱，從而更客觀地描述網絡的結構。

首先對指揮網絡涉及的術語做如下定義。

定義1:各級指揮機構為網絡節點。

定義2:指揮機構之間的信息交流關系為網絡的邊，并簡化為無向單線邊。

定義3:節點之間的信息流對作戰任務的貢獻程度為邊的權值(簡稱邊權)。

設G={V，E}，為由n個節點、m條邊構成的指揮網絡的加權圖，其中:V={v1，v2，…，vn}，為節點集合;E={e1，e2，…，em}，為邊的集合;

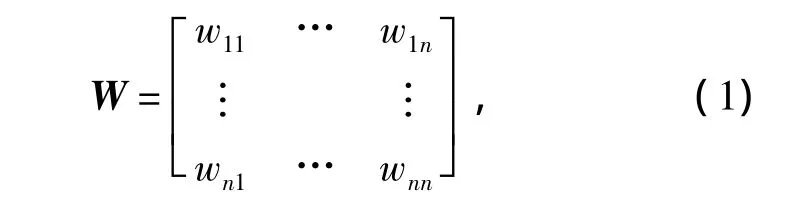
為鄰接節點之間邊的權值矩陣，wij為鄰接節點之間邊的權值。

把實際系統抽象為加權網絡需要考慮邊權的賦值方式，一般有相異權和相似權2種賦權方式［5］，對于相異權，權值越大，表示節點間的距離越大，關系越疏遠;對于相似權，權值越大，表示節點間的距離越小，關系越親密。在加權網絡中，由于邊權的存在，網絡節點間的距離一般不再滿足三角不等式，因而導致最短距離路由發生變化。如設節點vi、vk、vj通過權值為wij和wkj的邊相連，若采用相異權，節點間的距離可直接取和為dik=wij+wkj;而采用相似權，節點間的距離需要使用調和平均值dik=wijwkj/(wij+wkj)。本文采用相似權，設Xij為節點vi與節點vj之間的信息流對作戰任務的貢獻度，則邊權值wij的取值如下:

本文設定指揮信息的上傳、下達均為無向圖，則權值矩陣對稱，即wij=wji。

1．2 指揮網絡的社區特征

復雜網絡具有社區特征，即整個網絡系統可分為若干個“社區”，每個社區由若干個關系密切的節點構成，因此同一社區內的節點之間的關聯相對頻繁且緊密，而不同社區之間的關聯稀疏且松散。指揮網絡系統為追求指揮信息優勢最大化，對協同對象和合作范圍具有局域選擇偏好性，即在小范圍內信息相互交流頻繁，而在全局范圍內的交流相對較少或者交流期望不高，因此整個指揮網絡系統的結構具有社區性，這一特征與部隊的實際情況是相符的。因為根據不同的作戰需求、裝備特點、地理條件等，可將作戰力量分解為不同的作戰集團，各個作戰集團又可再分解為若干個小的作戰集群，各個作戰集群通過上級的指揮與其他作戰集群的協同來完成作戰任務。因此，作戰集群作為一個作戰整體，在其內部信息交流頻繁，而與外部的信息交流相對較少。整個指揮網絡存在如下社區特性:

1)同一社區內(如同一戰略、戰術、戰役單元)的節點之間距離較短;

2)不同社區內(如地理位置或功能不同的作戰單元)的節點之間距離相對較大;

3)同一社區內的節點之間信息交流頻繁，而與其他社區內的節點之間的信息交流頻率較低，即節點通過本社區其他節點的概率較高，而通過其他社區節點的概率較低。

2 評估方法

指揮網絡的層次性決定了各個節點的重要程度各不相同。節點重要度與其位置有關，如“非要塞節點”和“要塞節點”，“非末梢節點”和“末梢節點”，“戰略節點”和“戰術節點”，它們的重要度顯然不同。作戰指揮網絡中節點的特殊性體現在:不同作戰任務對節點所在社區的依賴程度不同，導致了不同社區中位置相同的節點其重要度也有差異，因此，指揮網絡節點的重要度受網絡拓撲結構、作戰任務對社區的依賴度2個因素的共同影響。

2．1 作戰任務對社區的依賴度

首先對子任務、社區功能子集作如下定義。

定義4:子任務為針對一次作戰任務，綜合考慮裝備特點，按照作戰指揮原則，將其細化分解為能由社區直接執行并完成的基本任務序列，稱分解后的基本任務為子任務。本文假定一個社區為一個基本作戰單元，可獨立、直接執行一項子任務。

定義5:社區功能子集(V)為具有相同功能的社區集合，假設同一子集中各社區分別執行同一子任務的效果相同，即彼此間可相互作為備份。

作戰任務對社區的依賴度與任務分解、社區功能子集形成、社區選取有關。由于能直接執行子任務的社區所在的功能子集中有其他社區作為備份，且備份越多，某一社區的失效對子任務的損失越小，則任務對這一社區的依賴度也越小。假設作戰任務M 可分解為子任務 M1，M2，…，Mn，子任務 Mi對應的社區為lij，功能子集Vi中有ki個備份，則子任務Mi對社區lij的依賴度為

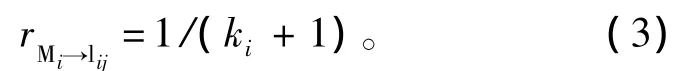
由于子任務對功能子集Vi中所有社區的依賴度相同，對非功能子集中社區的依賴度為0，因此，作戰任務M對社區lij的依賴度為

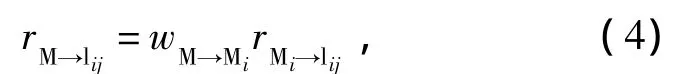
式中:wM→Mi為子任務Mi在任務M中的權重，由子任務Mi對作戰任務的重要度確定，假設 M1，M2，…，Mn的重要度依次為 PM1，PM2，…，PMn，則

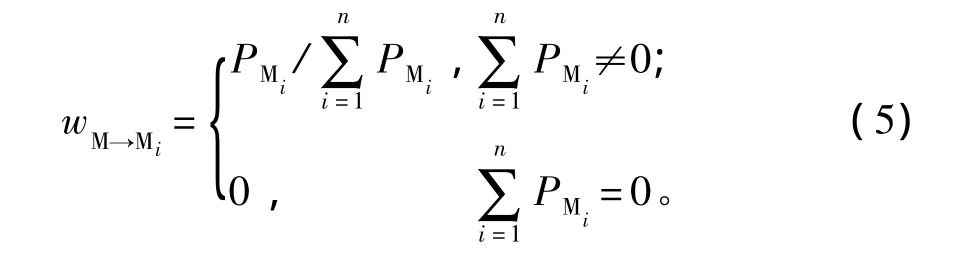
式中:子任務的重要度PM1，PM2，…，PMn可采用文獻［14］提出的基于內聚度和粒度的作戰任務分解評估方法求解。

2．2 節點相對重要度評價矩陣

網絡是由邊和節點構成的有機整體，表現在節點與節點間是互相關聯的，增加或減少節點都會導致其他節點的點權和載荷發生變化，因此，互聯互通的節點之間存在著一定的重要度貢獻拓撲關系，其結構為實際網絡的一個拓撲映射，本文采用節點重要度貢獻矩陣來表示節點之間存在的這種重要度貢獻拓撲關系。

文獻［15］定義了無權無向網絡的節點重要度貢獻矩陣，本文在此基礎上定義有權無向網絡的節點重要度貢獻矩陣(Node Importance Contribution Matrix In Weight Networks，NICMIWN)。在有 n 個節點、無自環、有權無向的網絡中，若節點vi的點權為si，vi對其每個鄰接節點vj的重要性貢獻度為wij/si，則當擴展到網絡中所有節點時，其對鄰接節點的重要性貢獻度可以通過加權網絡節點相對重要度貢獻矩陣來表示:

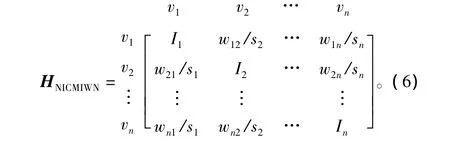
式中:對角線的Ik為節點vk的重要度初始值。

在作戰任務對社區依賴度確定的前提下，可將社區內的指揮網絡簡化為一般的網絡拓撲結構，其節點的重要度取決于節點位置、鄰接節點的重要度貢獻關系，本文采用點權來構建節點間的重要性貢獻關系;由于節點介數(Bn)由節點在網絡中的位置決定，因此，可用Bn反映節點vi的位置信息，矩陣HNICMIWN融合Bn后得到節點重要度評價矩陣:

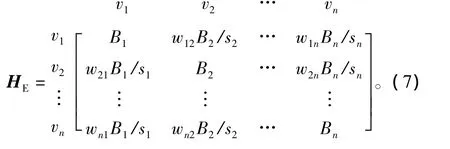
式中:元素HE(ij)表示鄰接點vj對節點vi的重要度貢獻。由式(7)可以看出:加權網絡中某一節點對鄰接節點的重要度貢獻取決于該節點的介數、點權、邊權值。

應用節點相對重要度評價矩陣，綜合考慮節點介數、鄰接節點重要度貢獻，計算節點vi在其所在社區內的相對重要度

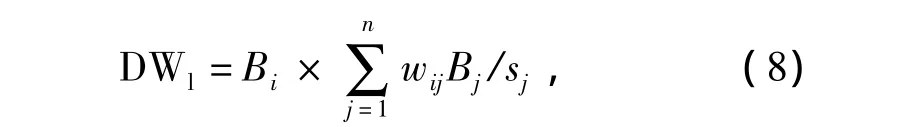
式中:sj為節點vj的點權，

Nj為節點 vj的近鄰集合;Bi為節點 vi的介數［16］，

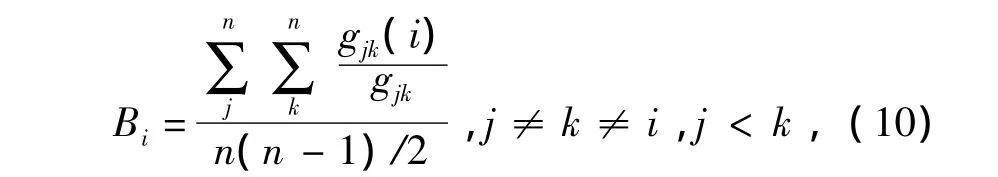
gjk為兩節點之間的最短路徑數，gjk(i)為經過節點vi的最短路徑數，n為節點總數。

2．3 節點全局重要度評價

節點全局重要度評價綜合考慮了作戰任務對社區的依賴度、節點在所在社區中的相對重要度2方面的因素。評估思路為:1)從全局出發將整個指揮網絡分割為一系列社區，給出各社區相對于作戰任務的重要度排序，即作戰任務對社區的依賴度;2)根據節點在社區的位置信息、鄰接節點的重要度貢獻關系，給出節點在社區的相對重要度;3)計算節點的全局重要度，即作戰任務對社區的依賴度與節點在社區的相對重要度乘積;4)遍歷所有節點，得出全部節點的全局重要度。具體步驟如下。

輸入，加權圖G和給定任務M;輸出，節點相對重要度和全局重要度。

1)將作戰任務M分解為子任務M1，M2，…，Mn，根據式(3)-(5)計算作戰任務對社區的依賴度rM→lij，即社區相對于作戰任務的重要度。

2)根據式(6)確定節點在社區內的相對重要度貢獻矩陣。

3)根據式(7)確定節點在社區內的相對重要度評價矩陣。

4)根據式(8)計算每個節點vj(j=1，2，…，ni，ni為社區lij內的節點數)在該社區lij內的相對節點重要度DWl。

5)計算所有節點的全局重要度DW(vj)=rM→lij×DWl，j=1，2，…，N，N 為整個網絡中所有的節點數。

3 案例分析

以防空部隊指揮節點為例，依據現行編制體制，將旅級單位作為一個社區規模，依據裝備類型劃分社區功能子集，每類裝備包含若干社區，假設某一社區lk的指揮網絡由4層指揮節點組成，如圖1所示。

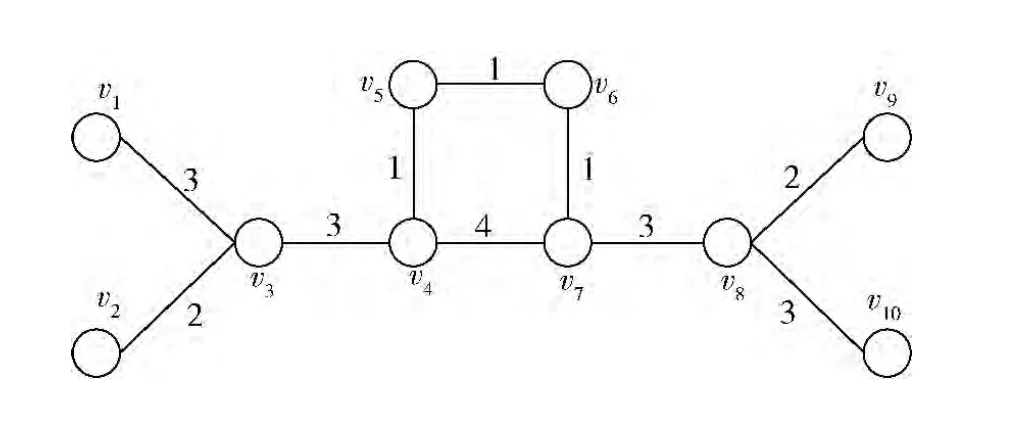
圖1 社區l k加權網絡拓撲結構

網絡中有10個節點和10條邊，根據式(9)、(10)得出網絡中各節點的點權和介數，并對應填入節點相對重要度評價矩陣HE中，得出

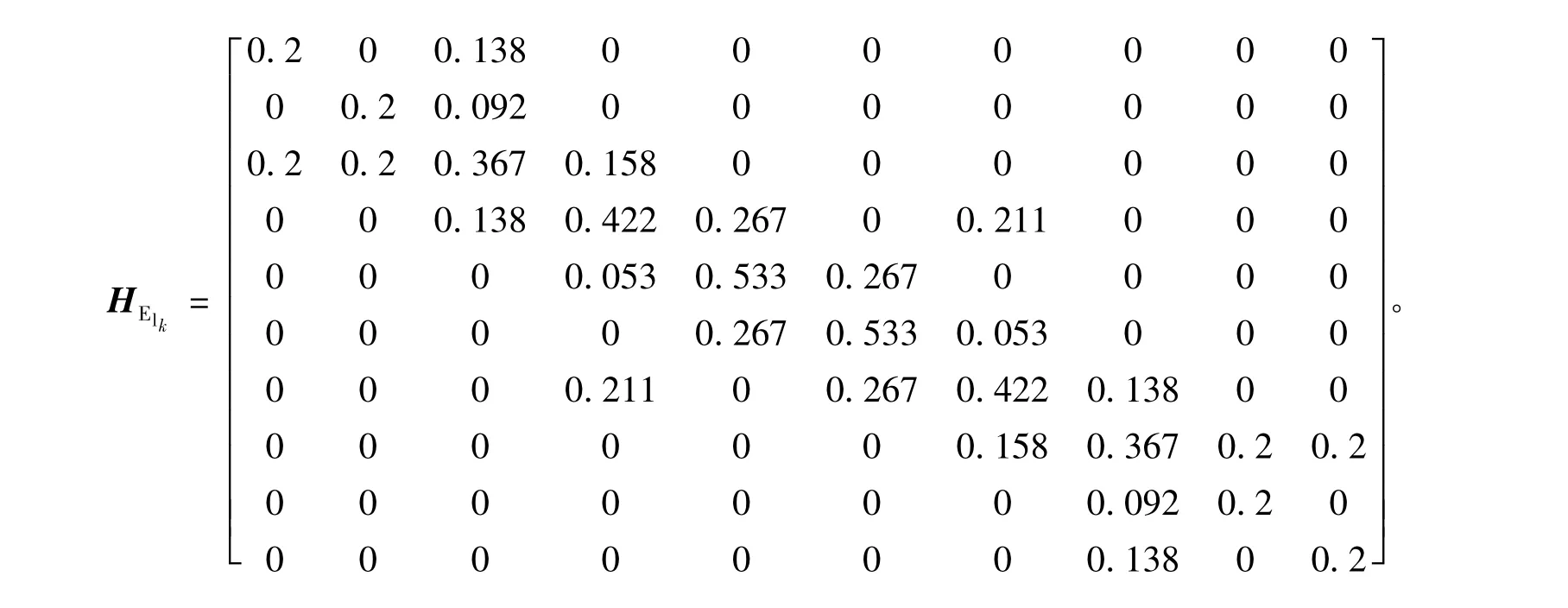
以節點v5為例，通過評價矩陣HElk可得出節點v5在社區lk中的相對重要度DWlk(v5)=0．533×(0．053+0．533+0．267)=0．454 ，同理，可得出其他節點的相對重要度。

表1為采用本文算法計算的社區lk內節點相對重要度評價結果，與介數方法、文獻［5］方法、文獻［6］方法的評價結果的對比分析，以及社區lk、lg節點全面重要度評估結果。由表1可以看出:1)本文算法與介數方法、文獻［6］方法有差異，介數方法不考慮邊權，因此無法進一步刻畫節點1、2、9、10之間的重要度差異，精度比本文算法稍差，文獻［6］方法在節點3、4、5、6、7、8的重要度排序與其他3種算法均有差異，原因在于文獻［6］的方法中引入了邊重要度系數，給出節點與邊系數比值以便重點考察節點重要度，但是邊的引入意味著計算結果是將節點、鄰邊作為整體并與其他整體進行比較，無法將節點剝離出來;2)文獻［5］的方法與本文算法的結果一致，得出節點5和節點6為最重要節點，但本文算法不涉及歸一化運算、矩陣乘法，運算量相對較小。

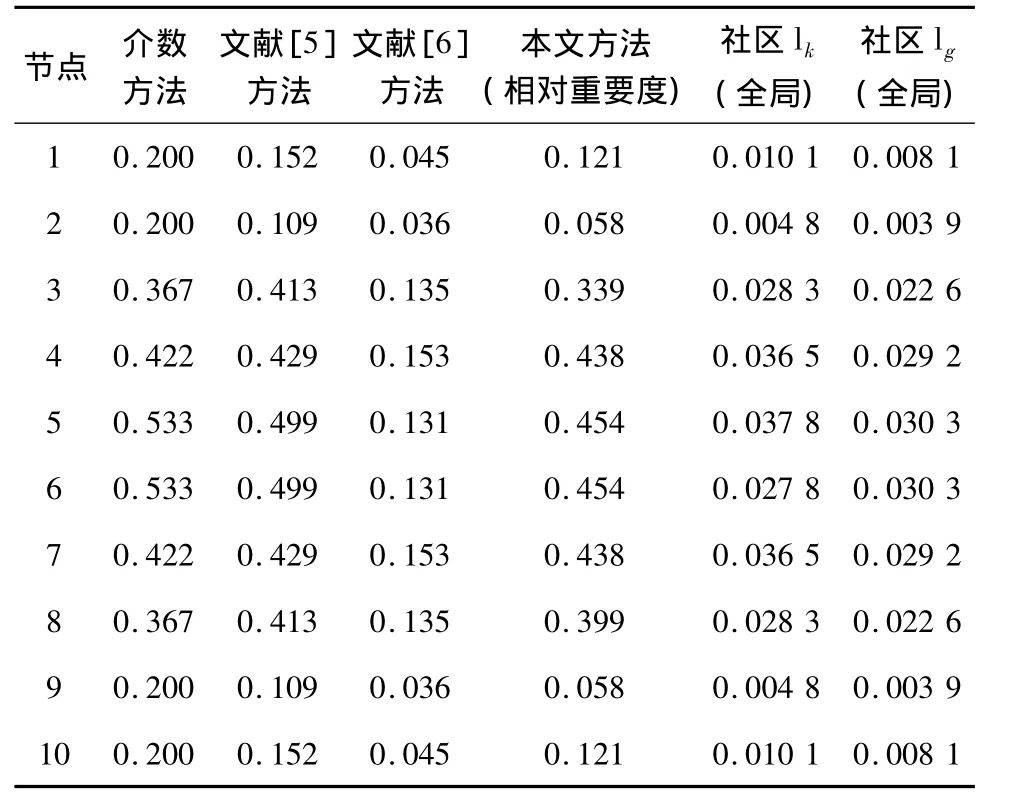
表1 社區l k內節點相對重要度的評估結果、與其他方法計算結果的對比及節點全局重要度評估結果

為了說明節點的全局重要度，本文假設針對一次作戰任務存在2個指揮結構、規模相同的社區lk、lg，且分別隸屬于A型和B型裝備形成的社區功能子集，其中A型社區功能子集中有3個備份，B型社區功能子集中有4個備份，并假設任務M可分解為子任務 M1，M2，M3，子任務重要度都為 1，則任務 M對社區 lk、lg的依賴度分別為 rM→lk=(1/(3+1))(1/(1+1+1))=1/12，rM→lg=1/15，結合節點在社區內的相對重要度，則2個社區節點的全局重要度如表1中社區lk和社區lg兩列所示，可以看出:隸屬于不同功能子集，但指揮結構相同的社區在應對同一任務時，節點全局重要度出現差異，這一結果與實際作戰情況相符，也表明算法是有效的。

4 結論

本文基于無權網絡無法深入刻畫指揮網絡中節點間相互關系細節，不能真實反映網絡結構特點的難題，研究了基于加權網絡模型的指揮節點重要度評估方法，本文的算法是在靜態網絡模型下建立的，下一步，將對包括節點增加、刪除以及邊權隨時間變化而變化的動態網絡展開進一步研究。

［1］ 賈子英，侯學隆，潘大志．網絡化防空體系中作戰單元重要度評估［J］．現代防御技術，2013，41(5):12-16．

［2］ 李玉華，賀人貴，鐘開，等．動態加權網絡中節點重要度評估［J］．計算機科學與探索，2012，6(2):134-144．

［3］ 陳勇，胡愛群，胡嘯．通信網中節點重要性的評價方法［J］．通信學報，2005，25(8):129-134．

［4］ 譚躍進，吳俊，鄧宏鐘．復雜網絡中節點重要度評估的節點收縮方法［J］．系統工程理論與實踐，2006(11):79-84．

［5］ 朱濤，張水平，郭戎瀟，等．改進的加權復雜網絡節點重要度評估的收縮方法［J］．系統工程與電子技術，2009，31(8):1902-1905．

［6］ 王甲生，吳曉平，廖巍，等．改進的加權復雜網絡節點重要度評估方法［J］．計算機工程，2012，38(10):74-76．

［7］ 張健沛，李弘波．基于拓撲勢的網絡社區節點重要度排序算法［J］．哈爾濱工程大學學報，2012，33(6):745-753．

［8］ 于會，劉尊，李勇軍．基于多屬性決策的復雜網絡節點重要性綜合評價方法［J］．物理學報，2013，62(2):020204-1-020204-9．

［9］ Callaway D S，Newman M E J，Strogatez S H，et al．Network Robustness and Fragility:Percolation on Random Graphs［J］．Physical Review Letters，2000，85(25):5468-5471．

［10］ Budanisky A，Hirst G．Evaluating Word Net-based Measures of Lexical Semantic Relatedness［J］．Computational Linguistics，2006，32(1):13-47．

［11］ Newman M E J．A Measure of Betweenness Centrality Based on Random Walk［J］．Social Networks，2005，27(1):39-45．

［12］ 王欣，姚佩陽，周翔翔，等．指揮信息系統網絡節點重要度評估方法［J］．北京郵電大學學報，2011，34(4):38-43．

［13］ 李茂林，龍建國，張德群．基于復雜理論的作戰體系節點重要性研究［J］．指揮控制與仿真，2010，32(3):15-19．

［14］ 董濤．基于智能算法的作戰任務分解評估研究［D］．西安:空軍工程大學，2013．

［15］ 周漩，張鳳鳴，李克武，等．利用重要度評價矩陣確定復雜網絡關鍵節點［J］．物理學報，2012，61(5):050201-1-050201-7．

［16］ 趙毅寰，王祖林，鄭晶，等．利用重要性貢獻矩陣確定通信網絡中最重要節點［J］．北京航空航天大學學報，2009，35(9):1076-1081．