課堂上那一條無形的“線”

趙紅婷

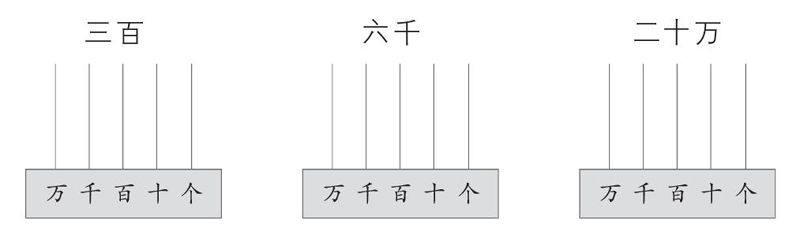
認識整萬數，其實質是對數位結構的整體把握。從萬以內數到整萬數，這是認數的一次飛躍，也是數級的一次拓展。不管是認數、讀數，還是寫數，都與數位結構息息相關。課前，周老師設計了四個問題，引領學生開展小研究，課堂上的大多數時間，師生都在交流展示，看似隨意，但形散而神不散，適時的點撥透露著深意。教師抓住了一條無形的“線”——數位結構，以數位結構的拓展、對應、分隔貫穿始終，使課堂教學達到了一定的深度。

一、撥數矛盾：實現數位結構的拓展

一位學生上臺匯報交流小研究第1題。

生：我用畫算珠的方法，在下面的計數器上表示相應的數。

學生呈現了前兩個數撥珠方法，對于撥20萬，她發現數位不夠，就在旁邊畫了一根豎線，并在上面撥了兩顆珠子。請別人補充，有學生說，新添的數位是十萬位。

教師特意請該班馮博士同學上臺展示小研究，他原本是在萬位撥了20顆珠子，但上來展示時卻已擦掉。教師及時抓住了這個例子，即使已擦去，仍讓學生觀察20顆珠子的印痕，學生認識到：如果萬位上放20顆珠子，能表示20萬。

教師設問：“萬位上的20顆珠子，相當于十萬位上的2顆珠子，它們之間是什么關系？”一學生說：“滿十進一。”因而得出：萬位和十萬位之間的進率是10。教師說：“這兩個計數單位只是冰山一角，能向左邊看看，再向右邊看看嗎？”隨著學生回答，教師板書了個級和萬級的計數單位，并標出了相鄰兩個單位之間的進率。

【賞析】小研究第1題的設計，體現了教師的匠心獨具。前兩個數是復習舊知，第三個數意在激起矛盾，讓學生感受數位拓展是必須。在最高位是萬位的計數器上，撥20萬，大多數學生都想到添加一個十萬位。但教師并不滿足于此，他發現一位學生的做法，即在萬位上撥20顆珠子。在辨析中，使學生認識到：萬位上的20顆珠子，相當于十萬位上的2顆珠子，萬位和十萬位之間的進率是10。隨著數的位數逐漸增多，新的數位將不斷出現，教師順勢引導學生從個級數位拓展到萬級數位，原有的數位結構便得到拓展和更新。

二、寫數對比：凸顯數位結構的對應

一位學生上臺交流第2個研究問題，具體如下。

師：怎么寫整萬數呢？結合下面的例子介紹我的方法。

例如，南京市目前常住人口大約是八百萬人，這個數寫作________________________________________________。

這個數寫作：________________________________________________ 。

我的方法是：________________________________________________。

這個學生舉的例子是：武漢大約有人口一千三百萬，寫作：13000000。他的方法是：先寫1300，再寫四個0。另一學生上臺補充：一套豪華別墅一千萬，寫作10000000。她的方法是：先寫后面的四個0，再寫前面的數。教師肯定了兩位學生的做法，鼓勵學生上黑板貼出數位，并寫出八百萬和一千萬。

接著，教師報數，學習練習寫數，依次是如下各數：

八十五 八十五萬

八百五十 八百五十萬

八千五百 八千五百萬

教師：“從左往右看，你是不是有話說？”學生：“右邊數比左邊數多4個0。”教師：“多了個‘萬字，就多了4個0。從上往下看，有什么特點？”學生：“右邊的數都有四個0。”揭示整萬數后，教師又追問：“整萬數末尾都只有四個0嗎？”學生持反對意見，學生：“不是，整萬數可能有4個0。”師生經過互相爭論和補充，得出：凡是整萬數末尾至少有4個0。

【賞析】小研究的第2題重在研究寫數方法。學生掌握寫法后，教師組織學生進行寫數對比。橫向對比使學生意識到，后者只比前者多一個“萬”，寫數的前一部分都是一致的，后者只要多寫4個0。縱向對比，學生更清晰地認識到，右邊是整萬數，它們末尾至少有4個0。這樣的縱橫對比，溝通了個級與萬級數位的聯系，雖然數級不同，但相關數位的對應關系卻是一致的。學生雖未能言傳，但他們已隱約意識到，整萬數前一部分的書寫，跟萬以內數的寫法是一致的，只需在后面添4個0即可。凸顯數位結構之間的對應關系，對學生認數、寫數都至關重要。

三、讀數求簡：突出數位結構的分隔

學生上臺匯報小研究的第3個問題，具體如下。

生：怎么讀這個整萬數呢？結合下面的例子介紹我的方法。

例如：一輛奔馳車的價格是1240000元，這個數讀作：________________________________________________。

________________________________________________。

我的方法是________________________________________________。

一位學生上臺讀出了汽車的價錢，舉出自己的例子，并介紹了自己的方法：先讀前面的數，再讀萬。

教師：“怎樣讀數更簡便呢？”教師特意請另一位學生上來交流，他說：“只要在千和萬之間畫一條豎線，我一看就知道了！”教師：“這樣畫豎線好嗎？畫豎線是不是隨便畫的？幾個0才能換一個萬？”師生交流后得出：在千位和萬位之間畫一條豎線，這便是個級和萬級的分級線。

【賞析】小研究的第3題主要解決讀數問題。對學生而言，讀數的難度要比寫數更大，因為讀數首先要將整萬數進行分級。教師并未直接介紹數位的分級，而是讓學生在讀數中感受分級的必要性。在師生的交流補充中，學生達成共識：要在千位和萬位之間畫分級線。事實上，分級線看似細小、微不足道，但對于構建正確的數位結構，起著非常關鍵的作用。數位的分級是一種分隔，但更是一種統整，分級線雖將個級和萬級予以區分，但其潛在的對應關系卻愈加分明，因此，分級既有分的思想，更有合的韻味。

四、玩數活動：內化數位結構的特質

學生上臺交流小研究的第4題，題目如下。

認識“整萬數”這部分內容中，有的題目特別好，我來給大家推薦一道。（可以從課本或資料中找現成的，也可以自己編）

解決了兩位學生設計的題目后，教師請幾位學生參與擺數游戲，用9、5、3、0、0、0擺一個整萬數，呈現：953000。教師：“你們有什么想說的？”學生：“少了一個0。”教師給出兩個0，學生貼出：95300000。教師：“只能這么擺嗎？”學生又將數改為：59300000，39500000。教師提示：后面的5個數能動嗎？于是，學生擺成：39050000。教師：“動來動去，有的地方一直沒動，哪些數不能動？”學生發現，最后四個0沒有動。教師鼓勵學生擺出一個最大的整萬數和一個最小的整萬數。學生都很容易擺了出來，接著教師說：“允許有些數字卡片下崗，擺出最小的整萬數。”幾位學生頗費了些周折，先是呈現了3050000，最后終于大膽擺出了30000。

【賞析】第4個小研究題目，旨在鼓勵學生與教師一起設計或搜集題目。解決了兩個學生的典型題目后，教師跟學生做起了擺數游戲。一開始，教師故意給學生6張數字卡片（其中僅三個0），學生馬上發現少了一個0，此處再次強化：整萬數的末尾要有4個0。接下去，教師給了學生兩個0，學生貼出一個最大的整萬數后，教師鼓勵學生改變數。教師問：“動來動去，有的地方一直沒動，哪些數不能動？”這個問題極為絕妙，讓學生再次感受到整萬數的數位結構，即整萬數末尾至少要有4個0。接著，教師鼓勵學生讓一些卡片“下崗”，最后呈現“30000”，再次凸顯：整萬數末尾至少要有4個0。這是整萬數最顯著的特征，教師通過一個擺卡片游戲，將整萬數數位結構的特征再次凸顯，收到了意想不到的效果。

（作者單位：江蘇省張家港市云盤小學 責任編輯：王彬）