用BP-PLS方法評(píng)價(jià)城市路側(cè)帶行人服務(wù)水平

李 嘉，鄧 敏

(1.西安市政設(shè)計(jì)研究院，陜西 西安 710068；2.合川區(qū)市政設(shè)施管理處，重慶 401520)

當(dāng)下，世界各國(guó)的城市交通領(lǐng)域均在提倡節(jié)能減排、綠色出行，而步行又是其主要的形式，因此步行交通系統(tǒng)的服務(wù)水平高低在一定程度上決定了城市的發(fā)展。路側(cè)帶作為城市居民步行主要的交通設(shè)施，其服務(wù)質(zhì)量的好壞直接影響著城市步行交通系統(tǒng)的服務(wù)水平，該服務(wù)質(zhì)量通常用行人服務(wù)水平(Pedestrian Level of Service，PLOS)進(jìn)行評(píng)價(jià)。國(guó)外對(duì)PLOS做了很多研究，具有代表性的有通過行人通行能力對(duì)路側(cè)帶PLOS進(jìn)行評(píng)價(jià)[1]，通過研究環(huán)境因素對(duì)路側(cè)帶行人服務(wù)水平的影響，提出定性和定量指標(biāo)進(jìn)行評(píng)價(jià)[2]，及通過對(duì)步行舒適度和安全感的定性、定量分析對(duì)PLOS進(jìn)行評(píng)價(jià)[3]。國(guó)內(nèi)對(duì)PLOS的研究較少，一些學(xué)者以行人密度、速度與流量為主要指標(biāo)，提出了劃分等級(jí)標(biāo)準(zhǔn)的評(píng)價(jià)方法。這些方法大多采用多元線性模型計(jì)算PLOS評(píng)分進(jìn)行評(píng)價(jià)，而各評(píng)測(cè)變量相互間多為非線性關(guān)系，多元線性模型無法準(zhǔn)確處理其間的關(guān)系，且傳統(tǒng)評(píng)分不能全面體現(xiàn)使用者的滿意程度，使評(píng)價(jià)精度降低。筆者引入滿意度評(píng)測(cè)中使用很多的結(jié)構(gòu)方程模型(Structural Equation Model，SEM)[4]建立評(píng)測(cè)體系，用以反映路側(cè)帶行人服務(wù)水平，并用BP神經(jīng)網(wǎng)絡(luò)偏最小二乘法(Back Propagation Neural Networks-Partial Least Squares，BP-PLS)[5]對(duì)PLOS進(jìn)行評(píng)分計(jì)算，從而提高評(píng)測(cè)的精度。

1 研究對(duì)象

根據(jù)CJJ 37—2012《城市道路工程設(shè)計(jì)規(guī)范》的定義，城市道路車行道兩側(cè)的人行道、綠化帶以及公用設(shè)施帶等功能帶統(tǒng)稱為路側(cè)帶。筆者研究對(duì)象即為城市道路普通路段路側(cè)帶的行人服務(wù)水平。

2 行人滿意度評(píng)測(cè)體系

評(píng)測(cè)行人滿意度所采用的結(jié)構(gòu)方程模型是一種建立、估計(jì)和檢驗(yàn)因果關(guān)系的模型，是由外部觀測(cè)樣本和內(nèi)部結(jié)構(gòu)模型組成，可同時(shí)考慮并處理多個(gè)因變量。模型中自變量(感知質(zhì)量)既包含可觀測(cè)的顯在變量，也可能包含無法直接觀測(cè)的潛在變量。因變量包括滿意度和忠誠(chéng)度兩個(gè)方面，Anderson模型和Kano模型分別反映了滿意度和忠誠(chéng)度、滿意度與感知質(zhì)量的非線性關(guān)系，如圖1。

圖1 Anderson模型及Kano模型Fig.1 Anderson model and Kano model

根據(jù)結(jié)構(gòu)方程模型的組成，設(shè)外部觀測(cè)樣本包括p個(gè)自變量(評(píng)價(jià)指標(biāo))(x1,x2,…,xp)和q個(gè)因變量(評(píng)價(jià)結(jié)論)(y1,y2…,yq)；內(nèi)部結(jié)構(gòu)模型與之對(duì)應(yīng)的包括m個(gè)潛在自變量(α1,α2,…,αm)和1個(gè)潛在因變量β。對(duì)應(yīng)模型結(jié)構(gòu)如圖2。

圖2 行人滿意度評(píng)測(cè)體系Fig.2 Evaluation system for pedestrian satisfaction

由于結(jié)構(gòu)方程模型在建模時(shí)對(duì)模型中各變量之間的關(guān)系均采用線性假設(shè)，而滿意度評(píng)價(jià)中各變量之間通常為非線性關(guān)系(圖1)，因此線性擬合會(huì)造成評(píng)估精度的降低。筆者用BP神經(jīng)網(wǎng)絡(luò)偏最小二乘法(BP-PLS)對(duì)各變量之間的關(guān)系進(jìn)行非線性擬合，可以解決線性模型難以合并交互作用，不能處理定性數(shù)據(jù)和數(shù)據(jù)缺失的問題。

3 BP-PLS建模

3.1 建模思想

BP網(wǎng)絡(luò)是一種多層前饋型神經(jīng)網(wǎng)絡(luò)，它主要被應(yīng)用于函數(shù)逼近、時(shí)間序列預(yù)測(cè)及模式識(shí)別。BP網(wǎng)絡(luò)算法首先是選取一組隨機(jī)數(shù)作為網(wǎng)絡(luò)的初始權(quán)值，再任意試取網(wǎng)絡(luò)的隱含層節(jié)點(diǎn)數(shù)和層數(shù)。若初始權(quán)值和隱含層節(jié)點(diǎn)數(shù)取值不當(dāng)，將會(huì)導(dǎo)致網(wǎng)絡(luò)陷入局部極小，使網(wǎng)絡(luò)訓(xùn)練速度減緩。偏最小二乘法是一種新型的多元統(tǒng)計(jì)數(shù)據(jù)分析方法，是S.Wold，等[6]在1983年首次提出的。它將多元線性回歸分析、典型相關(guān)分析和主成分分析結(jié)合起來，能夠處理多個(gè)因變量對(duì)多個(gè)自變量的建模問題，能夠克服變量多重相關(guān)性在系統(tǒng)建模中的不良作用。

筆者利用BP網(wǎng)絡(luò)算法能較好地?cái)M合非線性數(shù)據(jù)的特性，通過偏最小二乘法確定BP網(wǎng)絡(luò)的初始權(quán)值、隱含層數(shù)以及隱含層節(jié)點(diǎn)數(shù)，從而構(gòu)建一個(gè)基于非線性迭代偏最小二乘的BP網(wǎng)絡(luò)模型。該模型的優(yōu)勢(shì)在于能有效地確定網(wǎng)絡(luò)的初始權(quán)值、隱含層數(shù)及隱含層節(jié)點(diǎn)數(shù)，降低迭代次數(shù)，避免局部極小，使網(wǎng)絡(luò)計(jì)算精度最優(yōu)化。

3.2 偏最小二乘(PLS)原理與方法

PLS方法主要基于主成分回歸思想，首先尋求原始自變量x=(x1,x2,…,xp)的線性函數(shù)，分析它們與因變量y=(y1,y2…,yq)之間的相關(guān)性，選擇既便于計(jì)算，又與因變量相關(guān)性強(qiáng)的線性函數(shù)x，最后將新得到的自變量與因變量進(jìn)行回歸。由于它只偏愛與因變量有關(guān)的變量，所以未考慮全部的x1,x2,…,xp線性函數(shù)[7]。

PLS回歸是在x與y中分別提取成分t1和u1(其中t1是x1,…,xp的線形組合，u1是y1,…,yq的線形組合)。此時(shí)的t1與u1間具有相關(guān)程度最大、攜帶各自數(shù)據(jù)中變異信息程度最多等特點(diǎn)。

第1遍提取成分t1和u1后，回歸算法分別進(jìn)行x對(duì)t1及y對(duì)u1的回歸運(yùn)算。若回歸結(jié)果滿足預(yù)先設(shè)定的精度要求，則停止運(yùn)算；若不能滿足要求,算法，則用x被t1解釋后的殘余信息，和y被t1解釋后的殘余信息進(jìn)行第2遍成分提取。通過若干次循環(huán)，算法將自動(dòng)比對(duì)，判斷回歸結(jié)果是否滿足預(yù)先設(shè)定的精度要求。

PLS模型由求外部關(guān)系和內(nèi)部關(guān)系組成，x與y的外部關(guān)系有：

(1)

(2)

式中：T，U分別為x和y的主成分向量；P，Q分別為x和y的荷載矩陣；E，F(xiàn)分別為殘差矩陣。

x與y的內(nèi)部關(guān)系針對(duì)每個(gè)成分有：

(3)

(4)

PLS模型回歸具體步驟如下：

1)首先對(duì)數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理。x經(jīng)處理后的矩陣記為E0=(e01,e02,…,e0p)n×p，y經(jīng)處理后的矩陣記為F0=(f01,f02,…,f0q)n×q。

4)求得w1和c1后，可得到成分t1=E0w1和u1=F0c1，再分別求E0，F(xiàn)0對(duì)應(yīng)t1，u1的3個(gè)回歸方程：

E0=t1p1′ +E1

(5)

(6)

F0=t1r1′ +F1

(7)

5)用交叉有效性檢驗(yàn)增加成分t是否能夠顯著改善邊際貢獻(xiàn)值：

(8)

6)提取主成分個(gè)數(shù)及x，y的荷載矩陣P，Q。

3.3 BP-PLS模型

1)將原始自變量和因變量分為學(xué)習(xí)樣本和測(cè)試樣本兩部分。設(shè)原始自變量學(xué)習(xí)樣本矩陣x=(x1,x2,…,xp)和原始因變量學(xué)習(xí)樣本矩陣y=(y1,y2…,yq)分別為BP網(wǎng)絡(luò)的輸入矩陣和輸出矩陣。

2)用MATLAB內(nèi)置函數(shù)對(duì)原始數(shù)據(jù)矩陣進(jìn)行預(yù)處理，按先前所提及的PLS模型回歸方法逐步計(jì)算得到主成分個(gè)數(shù)、各主成分的系數(shù)回歸矩陣b以及荷載矩陣。

3)用主成分?jǐn)?shù)作為BP網(wǎng)絡(luò)的隱含層節(jié)點(diǎn)數(shù)，用x，y的主成分荷載矩陣P，Q作為網(wǎng)絡(luò)輸入層和輸出層的運(yùn)行初始矩陣，用x，y作為神經(jīng)網(wǎng)絡(luò)的輸入和輸出矩陣[8]。

4)構(gòu)建BP-PLS模型(圖3)，設(shè)定誤差目標(biāo)值，利用學(xué)習(xí)樣本訓(xùn)練網(wǎng)絡(luò)。

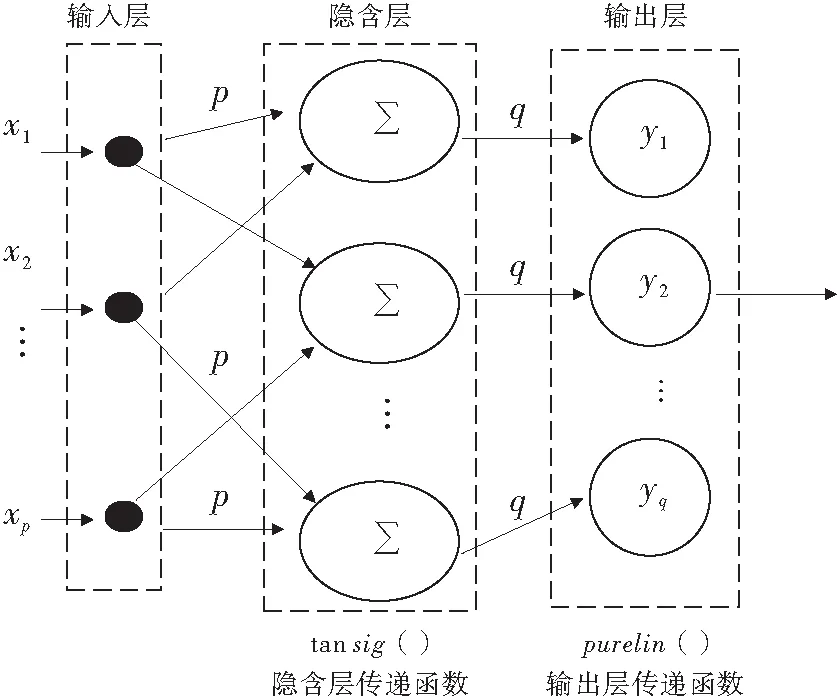
圖3 BP-PLS三層前饋神經(jīng)網(wǎng)絡(luò)示意Fig.3 BP-PLS three-layer feed forward neural network

5)網(wǎng)絡(luò)訓(xùn)練完成后，返回步驟1)～步驟3)，求測(cè)試樣本矩陣相應(yīng)的主成分?jǐn)?shù)及各矩陣。

6)將求得的測(cè)試樣本各數(shù)據(jù)逐一對(duì)應(yīng)輸入訓(xùn)練后的網(wǎng)絡(luò)，求得針對(duì)測(cè)試樣本的預(yù)測(cè)值。

4 模型實(shí)例分析

為了驗(yàn)證BP-PLS模型在路側(cè)帶行人服務(wù)水平(PLOS)評(píng)價(jià)中的有效性，利用文獻(xiàn)[9]的案例進(jìn)行分析。案例中調(diào)查人員通過不同時(shí)段實(shí)景拍攝、問卷調(diào)查(受訪者包括不同年齡階段)和專家評(píng)測(cè)，對(duì)主城區(qū)內(nèi)2條主干路10個(gè)路段街區(qū)的路側(cè)帶進(jìn)行了行人服務(wù)水平的評(píng)價(jià)研究，得出反映行人滿意度和行人忠誠(chéng)度的評(píng)分。

筆者按照行人滿意度評(píng)測(cè)體系，對(duì)案例中的各評(píng)價(jià)指標(biāo)進(jìn)行了歸納、分解，得到3個(gè)潛在自變量指標(biāo)：行人安全感知、行人舒適感知與步行空間效用感知，分別對(duì)應(yīng)10個(gè)顯在自變量指標(biāo)(x1,x2,…,x10)，如表1；因變量指標(biāo)則包括行人滿意度得分和行人忠誠(chéng)度得分(y1,y2)。因此，利用BP-PLS模型則有10個(gè)輸入因子，2個(gè)輸出因子。選取10組調(diào)查數(shù)據(jù)，其中8組作為神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)數(shù)據(jù)，2組作為測(cè)試數(shù)據(jù)。

表1 行人服務(wù)水平評(píng)價(jià)指標(biāo)

1)首先對(duì)學(xué)習(xí)數(shù)據(jù)進(jìn)行預(yù)處理，利用MATLAB計(jì)算得到交叉有效性判別結(jié)果，見表2。

表2 交叉有效性判別

2)構(gòu)建BP 三層前饋神經(jīng)網(wǎng)絡(luò)。根據(jù)第1)步求得的結(jié)果確定網(wǎng)絡(luò)結(jié)構(gòu)為10-2-2。輸入層采用S型函數(shù)，輸出層采用線性函數(shù)，x，y的主成分荷載矩陣P，Q分別為輸入層和輸出層的初始權(quán)值，用量化共軛梯度transcg()函數(shù)訓(xùn)練網(wǎng)絡(luò)。

3)通過迭代計(jì)算49次，誤差達(dá)到目標(biāo)值要求。利用訓(xùn)練后的網(wǎng)絡(luò)對(duì)測(cè)試數(shù)據(jù)進(jìn)行預(yù)測(cè)。

4)分別用PLS方法、BP模型以及BP-PLS模型對(duì)兩組測(cè)試數(shù)據(jù)分別進(jìn)行預(yù)測(cè)，通過測(cè)定系數(shù)R2對(duì)預(yù)測(cè)精度進(jìn)行檢驗(yàn)，結(jié)果見表3。

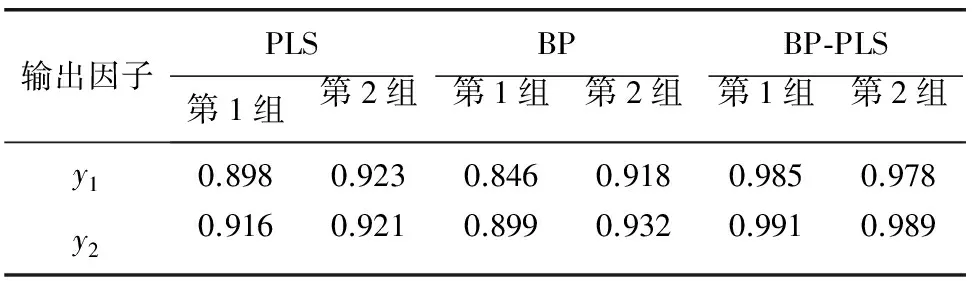
表3 3種方法R2比較

注：表內(nèi)數(shù)值為測(cè)定系數(shù)R2的值，R2越接近1，說明預(yù)測(cè)值越接近實(shí)際值。

從表3可以看出，3種方法擬合結(jié)果BP-PLS模型優(yōu)于PLS方法與BP模型，說明BP-PLS模型有比較好的擬合、預(yù)測(cè)功能。

5 結(jié) 語

用BP-PLS對(duì)路側(cè)帶行人服務(wù)水平的進(jìn)行評(píng)價(jià)。該方法將神經(jīng)網(wǎng)絡(luò)與偏最小二乘法結(jié)合起來，首先利用神經(jīng)網(wǎng)絡(luò)能夠很好地解決變量間非線性關(guān)系的特點(diǎn)，彌補(bǔ)了結(jié)構(gòu)方程模型的不足；其次，用PLS法提取原始樣本的主成分權(quán)值作為BP網(wǎng)絡(luò)的初始權(quán)值，提取主成分?jǐn)?shù)作為BP網(wǎng)絡(luò)隱含層的節(jié)點(diǎn)數(shù)，有效地提高了網(wǎng)絡(luò)的收斂速度，降低了迭代次數(shù)，很好地描述了因變量與自變量之間的關(guān)系，更易于解釋神經(jīng)網(wǎng)絡(luò)本身的含義。

從案例的預(yù)測(cè)結(jié)果可以看出，BP-PLS模型的預(yù)測(cè)精度最高，誤差最小，對(duì)實(shí)測(cè)數(shù)據(jù)具有較高的擬合精度和很好的預(yù)測(cè)效果。因此，可以作為一種行人服務(wù)水平評(píng)價(jià)方法。

[1] Fruin J J.Pedestrian Planning and Design [R].New York:Metropolitan Association of Urban Designers and Environmental Planners,1971.

[2] Dixon L B.Bicycle and pedestrian level-of -service performance measures and standards for congestion management systems[J].Transportation Research Record: Journal of the Transportation Research Board, 1996, 1538: 1-9.

[3] Landis B W,Vattikuti V R,Ottenberg R M, et al.Modeling the roadside walking environment: pedestrian level of service [J]. Transportation Research Record:Journal of the Transportation Research Board, 2001, 1773(1): 82-88.

[4] Stuart K R,Meduiek M,Bockman J.Structural equation model of customer satisfaction for the New York City subway system [J].Transportation Research Record, 2000, 1735(1): 133-137.

[5] Holcomb T R,Morari M.PLS/ neural networks [J].Computers & Chemical Engineering, 1992, 16 (4): 393-411.

[6] Wold S,Martens H,Wold H.The Multivariate Calibration Problem in Chemistry Solved by the PLS Method [M].New York: Springer Berlin Heidelberg,1983.

[7] 王惠文.偏最小二乘回歸方法及其應(yīng)用[M].北京:國(guó)防工業(yè)出版社,1999.

Wang Huiwen.Partial Least-Squares Regression-Method and Applications[M].Beijing: National Defense Industry Press,1999.

[8] Qin S J,McAvoy T J.Nonlinear PLS modeling using neural network [J].Computers & Chemical Engineering, 1992,16(4): 379-391.

[9] Dowling R, Reinke D, Flannery A, et al.Multimodal Level of Service Analysis for Urban Streets [R].Washington D.C.:Transportation Research Board, 2008.