岸橋并行作業效率約束下泊位與岸橋集成分派

高超鋒，胡志華,2

(1.上海海事大學 物流研究中心，上海201306；2.同濟大學 經濟與管理學院，上海 200092)

0 引 言

對于集裝箱碼頭，通過靠泊計劃和岸橋分派，及其集成分派優化船舶在港作業時間，不僅能夠降低運作成本，而且能夠提升整個運輸網絡系統的運作效率[1-4]。泊位與岸橋集成分派(Berth-Crane Allocation Problem，簡稱BCAP)是指船舶到港之前根據各個泊位的空閑情況和物理約束為船舶安排停靠泊位和靠泊順序，并配置岸橋。

泊位分派與岸橋調度通常作為兩個獨立的環節分別進行研究[5-7]。泊位分配與岸橋調度相互影響，將泊位分派與岸橋調度作為整體進行集成調度能夠提高港口碼頭的作業效率。A.Imai，等[8]考慮了岸橋移動路徑建立了同時優化離散泊位分配與岸橋調度的模型；Y. M. Park，等[9]建立了帶有偏離偏好泊位懲罰的最小費用泊位動態分配模型，并給出每個時間點為船舶作業配備的岸橋數量；M.Sammarra，等[10]建立岸橋作業順序和岸橋移動路徑優化的模型，采用禁忌搜索算法求解；R.M.Tavakkoli，等[11]給岸橋作業完成時間和船舶延遲到港時間賦予相應的權重，建立岸橋分派模型；P.Legato，等[12]考慮船偏好泊位和時間，以船舶作業時間和岸橋使用數量最少為目標建立泊位分派和岸橋分派模型。以上的研究僅從船舶在港等待時間，運作成本、偏好位置，岸橋移動路徑等角度考慮泊位—岸橋調度優化問題，很少涉及多臺岸橋同時作業的情況下，岸橋邊際效率減少的泊位與岸橋調度優化。

Y.M.Park，等[9]的研究表明，為一艘船舶同時服務的岸橋數量約為2～5臺。當為一艘船舶同時服務的岸橋數量大于1，則稱之為并行作業。分配給船舶的岸橋數量決定船舶掛靠以后的作業效率，船舶的裝卸作業時間和分配給它的并行作業的岸橋數量成反比，即岸橋數量越多，作業時間越短。但是，分配給船舶的單個岸橋的作業效率隨著并行作業岸橋數量的增多，因相互之間干擾增大而降低。靳志宏，等[13]將岸橋劃分為固定岸橋及調度岸橋兩子集，并且不同類型的岸橋作業效率不同，設計開發了遺傳算法，但沒有考慮多臺岸橋同時為一艘船舶工作時相互之間存在的干擾對岸橋作業效率的影響。F.Meisel，等[14]從靠泊位置的變化對岸橋作業效率產生影響和岸橋邊際效率減少的角度進行研究，但是沒有對每個時刻為船舶分配的岸橋數量變化對效率的影響進行分析，因為每個時刻船舶可用岸橋數量增加時，即并行作業的岸橋數量增加，相互之間干擾增大。C.J.Liang，等[15]考慮了岸橋配置數量對岸橋平均作業效率的影響，但是沒有考慮偏好泊位和并行作業岸橋相互的干擾。

不同數量的岸橋同時為一艘船舶工作時，對單個岸橋作業效率的影響不盡相同，相同數量的岸橋由于作業人員技術和作業環境的不同對效率的影響也不同，因此引入干擾因子研究船舶在港懲罰成本和岸橋作業時間的變化趨勢。另外，為了考慮偏離偏好泊位的影響，通過引入偏離最佳偏好泊位的懲罰系數來研究對船舶在港懲罰成本和岸橋作業時間的影響。最后，考慮多臺岸橋并行作業之間的相互干擾，研究并行作業的岸橋臺數對泊位與岸橋集成優化的影響。筆者對這些因素進行了綜合考慮、建模與分析。

1 問題描述

為了實現泊位與岸橋的集成調度，參照Y.M.Park，等[9]的研究，將泊位分配和岸橋分派問題用圖1的“時間-空間”表示。

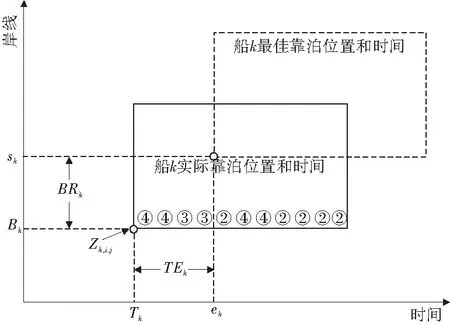
圖1 泊位岸橋集成調度Fig.1 Chart of berth-crane integrated scheduling

“時間-空間”圖由網格組成，一個網格表示一個單位時間和一個單位岸線，船舶占用網格表示在該事件和該位置進行裝卸作業。在圖1中，引入0/1變量Zk,i,j，表示船舶k是否從由靠泊時間j和靠泊位置i表示的位置開始作業。而方框表示該船舶占用的岸線(縱向)與作業的時間(橫向)，方框中圓圈中的數據代表每個時刻分配給該船舶的岸橋數量。

集裝箱港口根據船舶到港情況分配泊位。通常集裝箱都是暫時存放在堆場中，船舶靠泊時希望靠近其特定的堆場位置，這樣方便集卡把集裝箱從岸邊運送到堆場。這個位置相對應的岸線，即是船舶偏好的靠泊位置。如果實際分配的靠泊位置與最佳靠泊位置不一致，如圖1，將使集卡水平運輸距離增加，導致岸邊作業效率下降，船舶需要更多的岸橋工時。為此引入靠泊位置左偏離變量BLk和右偏離變量BRk，將靠泊位置和岸橋工時聯系起來，如圖2。

圖2 偏離最佳泊位懲罰成本Fig.2 Penalty costs off the optimal berthing position

定義Bk和sk分別表示船舶k的實際靠泊位置和最佳偏好泊位，從船舶左偏離量要求滿足約束BLk≥Bk-sk，船舶右偏離量要求滿足約束BRk≥sk-Bk。通過ak指定岸橋作業工時，則岸橋作業工時ak會因為作業效率的下降而隱性增加，可以表示為1+β(BLk+BRk)ak。β= 0.01表示若靠泊位置偏離其偏好位置1單位，其岸橋作業工時會隱性增加1%。船舶都有時間窗的約束，ek是船舶預期到達港口的時間，Tk是船舶實際到港時間，船舶提前到達港口的時間TEk=ek-Tk，推遲到達港口的時間TLk=Tk-ek，如圖3。

圖3 提前、推遲、延遲時間懲罰成本Fig.3 Penalty costs for time advancement and delay

當有多個岸橋同時服務于一艘船的時候，隨著岸橋數目的逐漸增多，岸橋的裝卸效率因為岸橋并行作業之間的干擾而產生變化。因此，引入岸橋干擾因子α，規定α≤1。ak表示完成船舶k作業需要的岸橋總臺時數，Yk,j表示j時刻分配給船舶k岸橋數量，把偏離最佳泊位的影響一起考慮，則需要滿足如式(1)的約束條件：

(1)

因為α≤1，所以需要增加岸橋數量或者延長船舶在港操作時間來抵消岸橋邊際效率減少的影響。隨著每個時刻的岸橋數的增加，則岸橋并行作業之間的干擾是怎樣變化，增加多少個岸橋才是合理的。如果延長船舶在港操作時間，則可能會造成船舶延遲離港，船舶延遲離港懲罰成本增加。

2 模 型

在模型中引入多臺岸橋同時工作的干擾因子α和泊位偏移系數β。如果多臺岸橋同時工作，相互之間存在一定的干擾，從而會降低岸橋工作效率。當船舶沒有停靠在偏好泊位時，同樣會對岸橋工作效率產生影響。為使模型設計與分析之便，將干擾系數與偏離懲罰系數設置為決策變量，即根據不同的岸橋數量產生不同的干擾率，根據偏離偏好泊位懲罰系數的大小產生不同的效率影響。并且，為重點研究干擾問題，考慮以下作業特征的泊位與岸橋集成分派問題：待靠泊的船舶沒有吃水和水深等約束；每條船都必須且只能靠泊一次，不考慮船舶靠泊后的移泊情況；船舶裝卸作業不能在中途停止；每艘船舶接受服務的岸橋數目有上下限制；若提供某個船舶服務的岸橋超過2個以上，則岸橋的工作效率受到影響。

2.1 集合、參數與決策變量

2.1.1 集 合

sl= {1，2，…，sls}，表示船舶序號集合，k，k-和k+表示其中的船舶；

sm={1，2，…，sms}，表示岸線分段集合，i，i-和i+表示其中的分段位置；

sn={1,2，…，sns}，表示時間分段集合，j，j-和j+表示其中的時段。

2.1.2 參 數

ek指定預期到達時間；

ak是以單位橋時計算的總的岸橋作業時間；

bk是船長；

dk是船舶離開的最晚期限；

sk是船舶的偏好泊位；

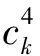
lk指定可以分配給船的最少岸橋數量；

uk表示能分配給船舶的最大岸橋數量；

c是港口可用岸橋的總數量。

2.1.3 決策變量

Xk,i,j是0/1變量，表示船舶k是否停靠在時空網格(i，j)作業，是為1，反之為0；

Zk,i,j是0/1變量，表示如果船舶k在時空網格(i，j)開始作業，是為1，反之為0；

vk,j表示船k是否在j時刻作業，是則為1，反之為0；

Uk,j表示船舶k是否占用位置i，是則為1，反之為0；

Yk,j表示在j時刻分配給船k的岸橋數量；

Ck表示船舶裝卸作業的完成時間；

BLk表示船舶在岸線維度的左偏離長度；

BRk表示船舶在岸線維度的右偏離長度；

TEk表示靠泊的提前時間長度；

TLk表示靠泊的推遲時間長度；

DLk表示相對于最晚離泊要求的延遲時間長度；

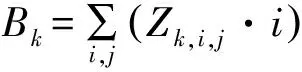
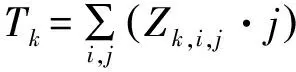
2.2 考慮岸橋并行作業效率約束BCAP模型

在Y.M.Park，等[9]的模型的基礎上，引入并行作業岸橋干擾因子和偏離偏好泊位的懲罰系數，構建船舶在港懲罰成本最小的泊位與岸橋的集成分派模型。

2.2.1 目標函數

最小化船在港總懲罰成本：

minf=(f1,f2,f3,f4)

(2)

2.2.2 約束函數

每艘船的操作時間要求必須滿足：

(3)

每一個時間段可供分配的岸橋數目不超過岸橋總數量：

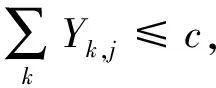
(4)

式(5)和式(6)定義Y和v之間的關系：

vk,j≤Yk,j,?k,j

(5)

Yk,j≤M·vk,j,?k,j

(6)

分配的岸橋數量，滿足可為該船舶服務的岸橋數量的上下限約束：

Yk,j+M·(1-vk,j)≥lk,?k,j

(7)

Yk,j≤uk,?k,j

(8)

離左邊最佳停泊位置的距離：

BLk≥Bk-sk,?k

(9)

離右邊最佳停泊位置的距離：

BRk≥sk-Bk,?k

(10)

提前到達時長：

TEk≥ek-Tk,?k

(11)

推遲到達時長：

TLk≥Tk-ek,?k

(12)

延遲離港時長：

DLk≥Ck-dk,?k

(13)

船舶離港時間必須在岸橋作業結束時間之后，即：

Ck≥vk,j·(j+1),?k,j

(14)

式(15)定義一個時空網格最多被一條船占用：

(15)

式(16)和式(17)約束v和X之間的關系：

(16)

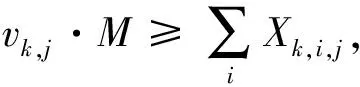
(17)

式(18)和式(19)約束U和X之間的關系：

(18)

(19)

式(20)保證船靠泊空間上的連續性：

(20)

式(21)保證船接受岸橋作業時間上的連續性：

(21)

式(22)約束v和Z在時間上的關系：

(22)

每艘船只能靠泊一次：

(23)

船靠泊在計劃的時空矩形內，Xi,j,k才能取值1：

?k,(sms-bk)≥i-≥2

(24)

定義船停靠位置的臨界條件：

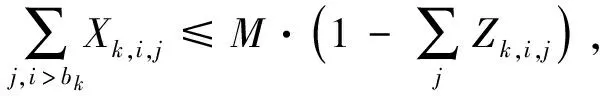
(25)

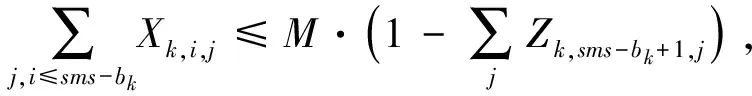
(26)

保證在時空網格圖中船舶靠泊矩陣的寬度等于船的長度：

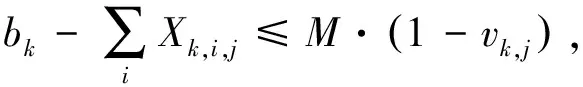
(27)

2.3 BCAP模型轉換

在2.2的模型中，式(3)是非線性的約束條件，下面把該約束條件轉換為線性約束。

在Meisel模型[14]的基礎上,將偏離最佳泊位分為左偏離和右偏離，這樣避免了Meisel模型計算泊位偏離的誤差，同時把偏離最佳泊位的懲罰成本作為目標函數，并且在算例中設定可用岸橋數量是變化的集合，用于分析在不同程度的干擾環境下岸橋數量變化對效率的影響。

在下面的模型中，引入以下變量：vk,j,q表示q個岸橋在j時刻分配給船舶k,則為1，否之為0；yk-,k+表示船舶k-在船舶k+之前靠泊，則為1，否之為0；zk-,k+表示船舶k-在船舶k+之前由岸橋開始對之作業，則為1，否之為0；定義岸橋數量集合R≡{q:lk≤q≤uk}，通過q進行索引。

2.3.1 目標函數

最小化船在港總懲罰成本：

minf=f1+f2+f3+f4

(28)

2.3.2 約束函數

多臺岸橋并行作業互相干擾及泊位偏移的影響下，須滿足每艘船的操作時間要求：

(29)

滿足最大岸橋數量限制：

(30)

每艘船舶作業開始與結束時間的關系如式(31)～式(33)：

(31)

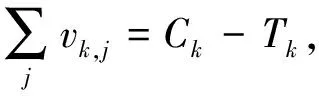
(32)

j·vk,j+sns·(1-vk,j)≥Tk,?k,j

(33)

兩艘船舶停靠的位置關系：

Bk++M·(1-yk-,k+)≥Bk-+bk-,?k-≠k+

(34)

兩艘船舶停靠時間的關系：

Tk++M·(1-zk-,k+)≥Ck-,?k-≠k+

(35)

避免兩艘船舶之間在停靠時間和停靠位置上的沖突：

yk-,k++yk+,k-+zk-,k++zk+,k-≥1,?k-≠k+

(36)

船離港時間必須小于最大時間窗：

Ck≤sns,?k

(37)

保證每艘船均停靠在岸線范圍內：

0≤Bk≤sls-bk,?k

(38)

3 算例與分析

以上海市洋山港集裝箱碼頭為例，驗證泊位與岸橋集成分派方法。泊位岸線長1 200 m，以50 m作為一個泊位單位，仿真服務周期48 h，1 h為一個時間單位。岸橋總數為16臺。同時為一艘船舶服務的岸橋數量有上下限約束，最小量是船公司和集裝箱碼頭簽署的合同決定，最大量是由可用岸橋數量決定。

為了模擬多船型的泊位與岸橋集成調度，列出了4種船型的相關參數。船舶到達時間ek隨機取自區間[1，35]，船舶偏好位置sk隨機取自區間[1，20]，船舶離開時間dk隨機取值([4，8] +ek)，船舶作業時間ak隨機取自區間[10，45]，不同類型的船舶參數取值范圍不同，如表1。

表1 種類型船舶的參數

3.1 靠泊位置對船舶在港懲罰成本和岸橋作業時間的影響

偏離最佳泊位的懲罰系數即偏離系數β在0～0.04之間依次遞增，岸橋可用數量集的范圍取[3，5]，即岸橋最大可用數量為5個，最小可用數量為3個，運行結果得到表2，岸橋總工時指每個時刻工作的岸橋數量總和，簡稱橋時。

表2 偏離最佳泊位的懲罰系數影響的計算結果

注：Δ=[(f2-f1)+(f3-f2)+(f4-f3)+(f5-f4)]/4。

由表2可知，隨著偏離最佳泊位懲罰系數增大，船舶在港懲罰成本平均增長率為12.07%，岸橋總工時平均增長率為1.39%。因為偏離最佳泊位的懲罰系數β增大，則1+β(BLk+BRk)ak增大，根據約束條件(3)就需要更多岸橋工時才能滿足，增加了船在港操作時間，相應的船在港懲罰成本增加；偏離最佳泊位同時會引起集卡交叉作業或者加長路線，則港口的運營成本增加。

偏離最佳泊位的懲罰成本沒有變化是因為懲罰系數一定的情況沒有改變整個集成調度系統的泊位分配，當不同船舶的懲罰系數不同時，則偏離最佳泊位的懲罰成本就會改變。

當β=0～0.02，隨著偏離最佳泊位懲罰系數增大，船舶提前到港的懲罰成本增加，而延遲離港成本減少。原因是隨著偏離最佳泊位懲罰系數增大，船舶在港操作時間增加，為了規避高額的延遲離港懲罰成本的增加，船舶會選擇提前到達港口。

當β=0.02～0.04，隨著偏離最佳泊位懲罰系數增大，船舶提前到港的懲罰成本減少，而延遲離港成本增加。這是因為船舶都有時間窗約束，不可能為規避高額的延遲離港懲罰成本，而使整個集成調度系統懲罰成本增加。

3.2 不同的作業環境對船舶在港懲罰成本和岸橋作業時間的影響

由于作業人員技術水平和作業環境的不同對效率產生的影響也不同。作業環境對并行岸橋作業效率的影響通過干擾因子來體現。在干擾因子α在1～0.8之間依次遞減，岸橋可用數量的范圍取[4，6]時，求解得到如表3的結果。

表3 干擾因子影響的計算結果

從表3可知，隨著岸橋并行作業干擾影響的增大(干擾系數的降低)，船舶在港的總懲罰成本f、偏離最佳泊位的懲罰成本、提前到港懲罰成本、推遲到港懲罰成本、延遲離港懲罰成本和岸橋總工時都是增大的趨勢。船舶在港的總懲罰成本f平均增加2 750元，岸橋總工時平均增加23.25 h。原因是隨著干擾增大，岸橋作業效率遞減，船舶所需岸橋工時增加，從而延長操作時間，需要安排船提前到港或者延遲船舶離港，增加船舶在港的懲罰成本。

船舶提前到港懲罰成本、延遲離港懲罰成本都與岸橋干擾影響正相關，而船舶延遲到港懲罰成本一直為0。原因是船舶到港時間比較集中，然而每艘船所需操作時間較大就會要求船提前到達港口，從而增加提前到港懲罰成本，避免高額的延遲離港懲罰成本。

船舶偏離最佳泊位的懲罰成本增加的原因是前一艘船舶在港操作時間延長，當船舶到達港口時，該船舶的最佳泊位被占用，所以船舶只能選擇偏離其最佳泊位的位置靠泊，從而增加船偏離最佳泊位的懲罰成本。

3.3 并行作業岸橋數量變化對船舶在港懲罰成本和岸橋作業時間的影響

設置偏離最佳泊位的懲罰系數為β= 0.01，干擾因子α在1～0.8之間依次遞減，岸橋可用數量的范圍在“[2，4]、[3，5]、[4，6]”依次變化，求解模型得到如表4的結果。

表4 并行作業岸橋數量變化的影響結果

注：Δf=((f|3-5|-f|2-4|)+(f|4-6|-f|3-5|))/2。

通過對表4進行分析發現，隨著每艘船舶可用岸橋數量的增加，船舶在港的懲罰成本f呈減少趨勢。Δf為負，表示船舶在港懲罰成本與可用岸橋數量呈負相關關系。并且發現，岸橋總工時與可用岸橋數量存在正相關關系，即隨著每艘船舶可用岸橋數量的增加，岸橋總工時增加。如圖4，岸橋可用數量為[4，6]是最下面的曲線，岸橋可用數量為[2，4]為最上面的曲線。

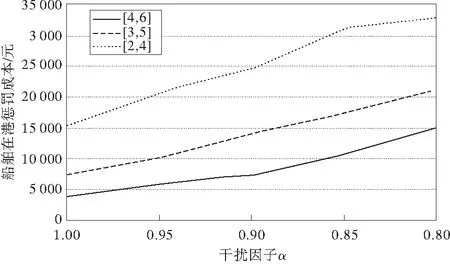
圖4 岸橋數量對船泊在港懲罰成本的影響Fig.4 Effect of cranes numbers on the penalty costs of vessel in port

當每艘船可用岸橋數量從[2，4]增加為[3，5]時，懲罰成本f平均減少43.83%，當岸橋可用數量從[3，5]增加為[4，6]時，懲罰成本f平均減少38.8%；因為船靠泊后并行作業的岸橋數量增加時，加快了貨物裝卸，則船舶需要的裝卸時間減少，相應的會減少船舶延遲離開港口時間，則延遲離港懲罰成本減少；或者因為操作時間減少，可以選擇船準時靠泊，則相應提前到港的懲罰成本減少。

如圖5，岸橋可用數量為[4，6]的曲線位于上方，岸橋可用數量為[2，4]的曲線位于下方，結果與圖4相反。

圖5 船舶在港岸橋總工時Fig.5 Cranes total operation time in port

當每艘船可用岸橋數量從[2，4]增加為[3，5]時，岸橋總工時平均增加4.65%，當岸橋可用數量從[3，5]增加為[4，6]時，岸橋總工時平均增加1.58%；因為同時為船舶并行作業的岸橋數量增加，岸橋相互之間的干擾更大，岸橋的裝卸作業效率降低，則船需要的總岸橋工時增加。

岸橋數量直接影響岸橋之間的干擾效率，岸橋并行作業的數量越多，則相互之間的干擾越大。雖然岸橋并行作業的數量較多時能夠加快船舶的裝卸，減少船在港操作時間，滿足船在計劃的時間內到港和離港的要求，減少船在港懲罰成本，但是卻增加了岸橋總工時，導致岸橋工作效率降低，增加港口能源消耗，使得集裝箱港口運作總成本增加。港口如何安排合理數量的岸橋為船舶作業，即要能夠滿足船靠泊時間窗約束，又要能夠避免分配的岸橋數量過多，導致并行作業之間的干擾增大，本文為決策者和船舶運營商在處理該問題時提供了解決矛盾的模型和依據。

4 結 語

在連續泊位與岸橋的集成調度模型的基礎上，研究岸橋并行作業時相互之間存在的干擾影響岸橋作業效率的問題。分配給同一條船舶的并行作業岸橋之間的干擾會影響岸橋作業效率；當船舶的偏離最佳靠泊位置時，同樣數量的岸橋并行作業產生的干擾大小是不同的。

筆者引入岸橋干擾因子和偏離最佳泊位懲罰系數來研究岸橋效率問題，建立了以船總在港懲罰成本最小的混合整數規劃模型。仿真分析發現，當岸橋可用數量確定時，隨著偏離最佳泊位懲罰系數增大，船舶在港懲罰成本平均增長為12.07%，岸橋總工時平均增長1.39%；隨著岸橋干擾因子變小船舶在港懲罰成本平均增長40.08%，岸橋總工時平均增長7.3%。分配給船舶的岸橋可用數量集增大時，船舶在港懲罰成本減小41.31%，但岸橋總工時增加3.12%，這兩者的矛盾邏輯上服從二律背反規律，服務與成本的矛盾，船公司希望少付費用而滿足自己所有的服務要求，而港口則希望在高質量服務時能夠得到高的效益回報。因此，集裝箱港口在集成調度中既要充分考慮并行作業的岸橋對服務質量的影響，同時還要充分考慮對作業效率的影響。下一步將在以下兩個方面繼續進行研究：建立岸橋干擾因子與岸橋分配數量的關系函數，利用啟發式算法進行求解大規模問題；根據岸橋作業的實時數據，研究在不確定性作業環境下岸橋并行作業對效率的影響。

[1] Monoaca M F, Sammarra M.The berth allocation problem: a strong formulation solved by a lagrangean approach [J].Transportation Science, 2007, 41(2): 265-280.

[2] Daganzo C F.The cranes scheduling problem transportation research [J].Transportation Research Part B: Methodological, 1989, 23(3): 159-175.

[3] 計明軍,靳志宏.集裝箱碼頭集卡與岸橋協調調度優化[J].復旦大學學報:自然科學版,2007,46(4):476-480.

Ji Mingjun, Jin Zhihong.A united optimization of crane scheduling and yard trailer routing in a container terminal [J].Journal of Fudan University:Natural Science, 2007, 46(4): 476-480.

[4] 周鵬飛,康海貴.面向隨機環境的集裝箱碼頭泊位-岸橋分配方法[J].系統工程理論與實踐,2008,31(1):161-169.

Zhou Pengfei,Kang Haigui.Study on berth and quay-crane allocation under stochastic environments in container termina [J].Systems Engineering Theory & Practice, 2008, 31(1): 161-169.

[5] Li C L,Cai X Q,Lee C Y.Scheduling with multiple jobs on one processor pattern [J].IIE Transaction,1998, 30(5): 433-445.

[6] Imai A,Nishimura E,Papadimitriou S.The dynamic berth allocation problem for a container port [J].Transportation Research Part B: Methodological, 2001, 35(4): 401-417.

[7] Gerald G B,Siriphong L,Katie P T.Optimizing ship berthing [J].Naval Research Logistics,1994, 41(1):1-15.

[8] Imai A,Chen H C,Nishimura E,et al.The simultaneous berth and quay crane allocation problem [J].Transportation Research Part E:Logistics and Transportation Review, 2008, 44(5): 900-920.

[9] Park Y M,Kim K H.A scheduling method for berth and quay cranes [J].Container Terminals and Automated Transport Systems,2003,25(1): 1-23.

[10] Sammarra M,Cordeau J F,Laporte G,et al.A tabu search heuristic for the quay crane scheduling problem [J].Journal of Scheduling,2007, 10 (4/5): 327-336.

[11] Tavakkoli-Moghaddam R,Makui A,Salahi S,et al.An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports [J].Computers & Industrial Engineering,2009,56 (1): 241-248.

[12] Legato P,Gulli D,Trunfio R.The quay crane deployment problem at a maritime container terminal [C]//Proceedings of the 22ndEuropean Conference on Modeling and Simulation.Campora San Giovanni, Amantea (CS),Italy: [s. n.], 2008: 53-59.

[13] 靳志宏,徐奇,韓駿,等.集裝箱碼頭泊位與岸橋聯合動態調度[J].中國科技論文在線,2011,11(6): 809-814.

Jin Zhihong,Xu Qi,Han Jun,et al.United dynamic scheduling of berths and quay cranes in a container terminal with consideration of actual constraints [J].Science Paper Online,2011,11(6):809-814.

[14] Meisel F,Bierwirth C.Heuristics for the integration of crane productivity in the berth allocation problem [J].Transportation Research Part E:Logistics and Transportation Review,2009,45(1):196-209.

[15] Liang C J,Huang Y F,Yang Y.A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning [J].Computers & Industrial Engineering,2009,56(3): Y1021-1028.