基于電阻法的鋼橋疲勞裂紋檢測方法研究

袁周致遠，吉伯海，傅中秋，劉 榮，程 苗

(河海大學 土木與交通學院，江蘇 南京210098)

近年來，交通基礎建設得到迅猛發展，各地興建了大量的大跨度鋼橋，但鋼材的自身特點在車輛荷載的反復作用下容易產生疲勞損傷。常用的探傷的方法主要有超聲波探傷、磁粉探傷及射線探傷。超聲波探傷對粗糙、形狀不規則、小、薄或非均質材料難以檢測。磁粉探傷只能針對表面或近表面的裂紋。射線探傷由于其器材費用高、對人體有傷害、且檢測速度慢、攜帶不方便，不易發現小裂紋而不適用于橋梁鋼面板的檢測。

目前，電阻法[1]探傷已經初步在許多領域應用起來，但更多地僅限于金屬構件的損傷檢測[2-4]、評定[5]及預測金屬材料疲勞壽命[6-7]，對于鋼橋面板疲勞裂紋檢測尚未研究和應用。筆者提出了基于電阻變化規律[8]來檢測鋼橋面板疲勞裂紋的方法，在理論與有限元分析基礎上，對測量影響因素及測點布置[9-11]方式進行的研究分析，通過U肋部位疲勞裂紋試驗驗證，并計算出檢測部位有效損傷率及斷面損傷面積，給出3種適合實際裂紋檢測的方法。

1 電阻法檢測原理

假設鋼板的標準電阻值為R0，實測電阻值為R1，則斷面損傷率D按式(1)計算：

(1)

對于電阻法檢測裂紋而言，其斷面損傷率D按式(2)計算：

(2)

式中：A0為斷面面積；A1為損傷面積。

根據斷面損傷面積A1和測點有效分布寬度b可推算裂紋的等效深度[12]h：

(3)

斷面損傷面積是針對每個測點而言的，如圖1。在水平鋼板上施加電流時，電流有一定的有效分布寬度b，其值的大小與兩電極之間的距離L有關，L越小，b值就越小。因此在合理的測點布置情況下，測點之間的距離B就可以作為有效分布寬度b的值。

圖1 有效分布寬度示意Fig.1 Effective distribution width

2 電阻法檢測影響因素分析

2.1 板 寬

板寬影響著電阻計算的邊界條件。圖2(a)表明：在同一電極間距下，板寬達到一定時，電阻值逐漸趨于平穩，該平穩點可以當作測點的有效分布寬度。不同電極間距對比看出電極間距越小，其趨于平穩的板寬越小。減小測點間距，能夠沿裂紋方向布置更多的測點，提高檢測的準確性。

2.2 電極間距

保持板寬不變，建立電極間距與測點電阻值之間關系，如圖2(b)。板寬越小，電阻值對電極間距的變化敏感性大；板寬越大，電阻值的變化幅度就越小。對于鋼橋面板來說，其板寬相對于電極間距，可以當作無窮大，即每組測點的邊界條件近乎是一致的。因此，在對隱蔽裂紋進行初步探查時，增大電極間距對于探測裂紋的靈敏度無多大影響。

圖2 電阻變化規律Fig.2 Variation of electrical resistance

2.3 裂紋附近測點有限元分析結果

有限元實體模型的尺寸為600 mm × 600 mm × 14 mm的平鋼板，中間設一短裂縫，如圖3。沿x軸方向每隔50 mm分別布置11個測點。得到11組電阻值，繪制成折線圖，見圖4。

圖3 帶裂紋平板有限元模型和測點布置情況Fig.3 Finite element model of deck with the crack and layout of measurement points

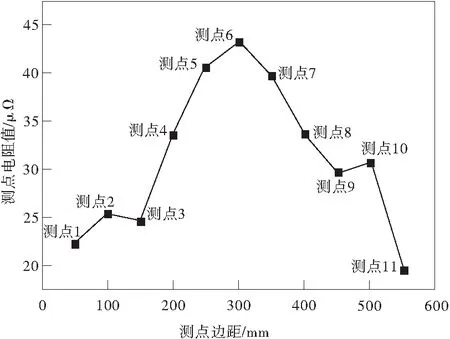
圖4 裂紋附近測點阻值變化規律Fig.4 Changing law of electrical resistance near the crack

從圖4看出，位于裂紋附近的電阻值比其它測點電阻值大，曲線呈現明顯的單峰。由此可以判斷曲線峰值附近對應的部位存在缺陷或裂紋。從圖4中曲線趨勢來看，裂紋存在于測點4～測點8之間。位于裂紋遠處的測點，如測點1～測點3，測點9～測點11的電阻值大小受單元劃分及鄰近測點電流干擾存在正常波動。

筆者針對電極間距分別為100，200 mm做了電阻值計算分析對比，如圖5。電極間距越大，曲線峰值越不明顯，裂紋判斷的準確度也會降低；但曲線峰值對應的測點邊距近似一致。因此，大電極間距只能夠用于初步掃查，確定裂紋初步位置，小電極間距用于準確定位和確定裂紋起始點。

圖5 不同電極間距下裂紋附近測點阻值變化規律對比Fig.5 Comparison of changing rule of electrical resistance near the crack with different electrode spacings

3 裂紋分布結果判斷

改變測點布置方式，以裂紋中心為圓心，電極間距為直徑，依次布置11個測點，如圖6。

圖6 環形電極有限元模型及測點布置Fig.6 Finite element model of annular electrode and layout of measurment points

繪制似“雷達圖”，如圖7。其中測點6的電阻值最大，測點1電阻值最小。從實際測點布置與裂紋開裂方向來看，測點6對應的方向近似為裂紋方向，通過尋找測點最大值可以判斷裂紋方向。增加測點數量，能夠提高準確度。

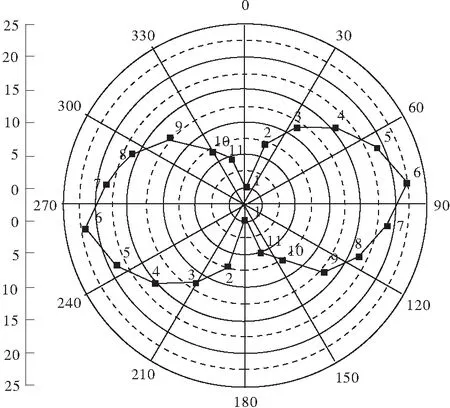
圖7 環形電極測點電阻值變化規律Fig.7 Changing law of annular electrode resistance at measurement points

4 電阻法裂紋檢測方法應用

4.1 測點設計

測點設計主要包括兩方面的內容：①開裂部位檢測的測點設計；②裂紋走向的測點設計。前者的作用是檢測是否存在裂紋，后者的作用是判斷裂紋的走向。

1)表面可見裂紋。由于其已經被發現，故可以直接在裂紋附近布置測點。對于1組探頭測量而言，可采用逐點測量法(圖8)，即沿著裂紋方向布置的測點逐個測量。對于多組探頭，可采用跳點測量法(圖9)，即先測量相隔1或2個測點上的電阻值，然后再回過來測量剩余點處的電阻值。

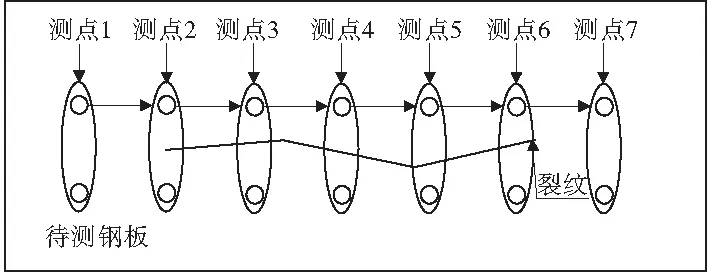
圖8 逐點測量法示意Fig.8 Point by point method

圖9 跳點測量法示意Fig.9 Jump point method

2)隱蔽裂紋。首先增大探頭間距，提高檢測范圍，待發現電阻變化后，采用逐步逼近法，減小探頭之間距離，提高檢測精度(圖10)。檢測到裂紋后，采用環形測點法(圖11)進行裂紋走向判定。測點最大阻值所對應的方向可近似作為裂紋開裂方向。沿著預判方向繼續測查，直到每個方向測點電阻值近似相等，將預判方向依次連接，即可當作裂紋延伸走向。

圖10 逐步逼近法測量示意Fig.10 Stepwise approximation method

圖11 裂紋走向測點布置Fig.11 Crack trend and layout of measurement points

4.2 試驗試件及裝置

本驗證試驗采用的雙臂電橋型號為QJ84A。試件材料為Q345鋼材，模擬鋼橋面板與U肋連接部位。該試件已經過疲勞試驗，在面板和U肋連接處產生沿U肋縱向的裂縫，如圖12。

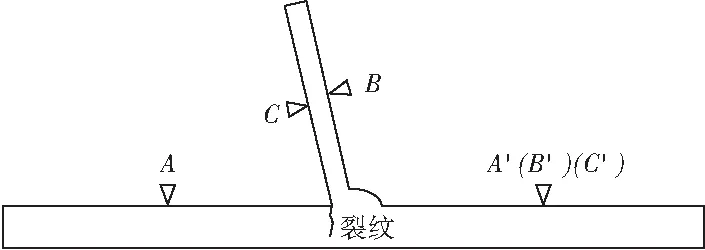
圖12 試件斷面Fig.12 Fracture of specimen

4.3 檢測結果分析

雙臂電橋裝置分別在U肋兩側(A、A′)、U肋外面(B、B′)、U肋內面(C、C′)布置。實測鋼板沿程電阻值數據如表1，沿程電阻變化如圖13。

表1 鋼板沿程實測電阻值

圖13 鋼板電阻沿程變化Fig.13 Electrical resistance of specimen

除去該異常點，可以看到其他測點電阻值的變化規律，如圖14。U肋兩側電阻值隨著測點邊距增大，曲線逐漸向上延伸。在測點邊距25.5 cm處電阻值達到最大。這說明沿著U肋縱向，裂紋深度增大，截面損傷嚴重。

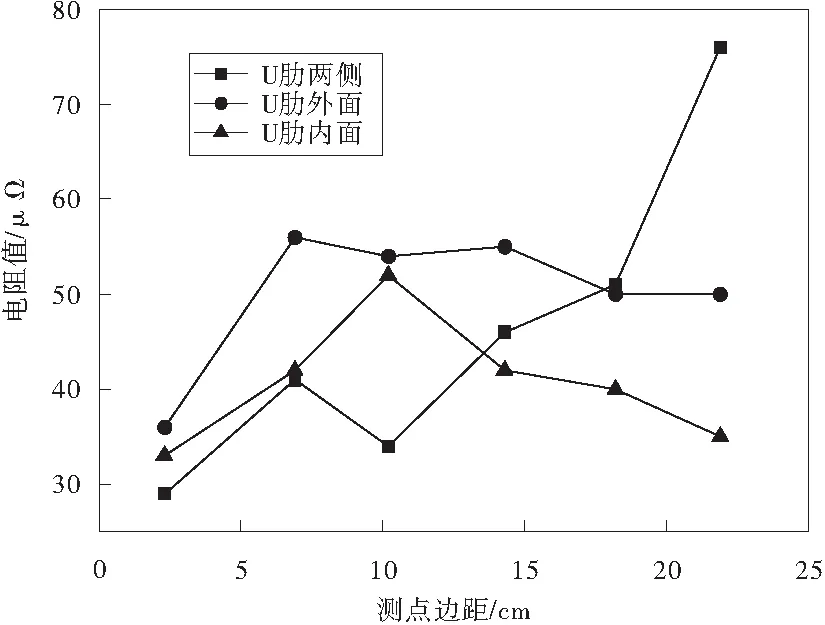
圖14 去除異常點后實測電阻變化規律Fig.14 Electrical resistance of specimen removing abnormal point

在U肋外面測點和U肋內面測點的電阻值，存在小幅波動，曲線峰值不明顯。考慮焊縫尺寸不均勻及測量誤差，相對于U肋兩側，可以認為U肋和頂板連接處不存在疲勞裂紋。這也符合實際鋼板疲勞裂紋開裂變化情況。

由式(1)、式(3)對U肋兩側分別計算截面損傷率D和裂紋等效深度h，結果如表2。

表2 截面損傷率和裂紋等效深度計算結果

試件實際厚度為1.4 cm。試件切割后通過斷面觀察疲勞裂紋，在測點邊距2.3 cm處幾乎不存在疲勞裂紋，把該處的阻值作為標準阻值。在測點邊距為25.5 cm處鋼板疲勞裂紋計算深度為1.32 cm，符合實際近乎裂透的情況，并有一定的鐵銹。因此在該測點的U肋實測電阻值相對于其他測點阻值異常，并且很大。

5 結 論

1)電極間距越小則檢測精度越高。在實際鋼橋面板疲勞裂紋檢測中，測點的邊界條件可以認為近乎一致，電極間距的大小對實測值的變化影響較小。因此大電極間距適合裂紋位置的初步判斷，小電極間距適合裂紋的精確定位。

2)對裂紋附近測點進行設計，建立裂紋分布結果的判斷方法并提出逐點測量法、跳點測量法、環形測點法3種測量方法，用于檢測裂紋開裂部位及判斷裂紋延伸方向。

3)對存在疲勞裂紋的試件進行測量，得到測點沿程變化情況。計算所得的斷面損傷率和裂紋等效深度符合鋼板實際裂紋深度情況，驗證電阻法檢測鋼橋疲勞裂紋方法具有較好的精度。

[1] 鄭慶華,童悅.雙臂電橋測低電阻[J].物理與工程,2009,19(1):36-38.

Zheng Qinghua,Tong Yue.Low resistance measurement by double bridge [J].Physic and Engineering,2009,19(1): 36-38.

[2] 唐文強.雙臂電橋測量低電阻中接線問題[J].儀器儀表用戶,2005,12(5):105-106.

Tang Wenqiang.Wiring question in double armed electric bridge measure low resistance [J].Instrumentation Customer, 2005,12(5):105-106.

[3] 孫斌祥,郭乙木.考慮電阻率變化的電阻法預測金屬材料剩余壽命[J].工程設計,2001(2):81-84.

Sun Binxiang,Guo Yimu.Estimation of remaining life of metallic materials by electrical resistance method considering variable resistivity [J].Engineering Design, 2001(2): 81-84.

[4] 黃丹,許平聰,郭乙木.金屬疲勞剩余壽命預測模型的一種探索[J].實驗力學,2003,18(1):113-117.

Huang Dan,Xu Pingcong,Guo Yimu.A research on the estimation of remaining service life for metals in fatigue [J].Journal of Experimental Mechanics, 2003,18(1): 113-117.

[5] 袁立方.基于電阻法的30Cr1Mo1V汽輪機轉子蠕變壽命研究[D].長沙:長沙理工大學,2007.

Yuan Lifang.Study of Creep Life of Steam Turbine Rotor Steel 30Cr1Mo1V Based on Electrical Resistance Method [D].Changsha: Changsha University of Science & Technology, 2007.

[6] 馬寶鈿,杜百平,朱維斗,等.電阻法檢測疲勞損傷及預測修復效果探討[J].理化檢驗:物理分冊,2002,38(11):493-495.

Ma Baotian, Du Baiping, Zhu Weidou, et al.Fatigue damage evaluation and repairing effect prediction by electrical resistance measurements [J].Physical Testing and Chemical Analysis Part A: Physical Testing, 2002, 38(11): 493-495.

[7] 黃丹,章青,郭乙木.電阻法檢測金屬構件損傷及預測疲勞壽命[J].無損檢測,2008,30(4):213-215.

Huang Dan,Zhang Qing,Guo Yimu.Damage measurement and fatigue life prediction for metallic components by electrical resistance method[J].Nondestructive Testing, 2008, 30(4): 213-215.

[8] 馬寶鈿,杜百平,朱維斗,等.從電阻變異規律分析疲勞損傷件中溫熱等靜壓效果[J].測試技術學報,2002,16(增刊1):337-340.

Ma Baotian,Du Baiping,Zhu Weidou,et al.HIP effect on fatigue damaged specimens by electric resistance variation [J].Journal of Test and Measurement Technology, 2002, 16(S1): 337-340.

[9] Todoroki A,Omagari K,Shimamura Y,et al.Matrix crack detection of CFRP using electrical resistance change with integrated surface probes[J].Composites Science and Technology,2006,66:1539-1545.

[10] Todoroki A,Tanaka M,Shimamura Y.Electrical resistance change method for monitoring delaminations of CFRP laminates [J].Composites Science and Technology, 2005, 65: 37-46.

[11] Jie Wen,Zhen Haixia,Choy F.Damage detection of carbon fiber reinforced polymer composites via electrical resistance measurement [J].Composites:Part B, 2011, 42: 77-86.

[12] 王苗苗,曾燕屏,王習術,等.航空用超高強度鋼疲勞裂紋表面長度與內部長度之間的關系[J].航空材料學報,2009,29(3):102-106.

Wang Miaomiao, Zeng Yanping, Wang Xishu, et al.Relationship between surface length and inside length of fatigue crack in ultra-high strength steel [J].Journal of Aeronautical Materials, 2009, 29(3):102-106.