多智能體系統初始狀態一致性應用研究

劉孝琪，康懷祺，曾超

電子科技大學電子科學技術研究院，成都611731

1 引言

近年來，隨著控制理論的發展，越來越多的研究者開始轉向多智能體系統一致性理論的研究，目前在無人機編隊、蜂擁控制、分布式控制中都有著廣泛的應用。對于復雜系統，利用傳統的控制方法來分析和控制是十分困難的，在這種背景下多智能體系統協調控制的發展是必然的。

在多智能體系統的一致性問題研究中，關鍵問題在于設計一致性控制律使得各智能體的狀態達到相同。隨著控制理論的發展，多智能體一致性的研究取得了一系列的成果。Vicsek等人[1]利用局部信息提出了一個自驅動模型描述平面粒子的運動；Jadbabaie等人[2]對Vicsek模型進行了線性化，分析了拓撲結構變化情況下的一致性問題；Ren等人[3]將Jadbabaie等人所得結果推廣到了有向圖；與Ren等人工作并行，M oreau[4]研究了有向圖非線性多智能體系統一致問題；Hong等人[5]研究了二階多智能體系統，基于局部信息提出了一個二階協議，將Jadbabaie等人的結果推廣到二階多智能體系統；文獻[6-9]研究了多智能體系統基于有向信息交換的分組一致問題。

目前，多智能體系統的平均一致性研究的比較早，成果也比較多，文獻[10]在考慮通信時滯和拓撲結構變化對系統狀態影響的基礎上，研究了平均一致性問題。但是，目前的研究針對多智能體初始狀態的一致性問題的還比較少。而現實中，多智能體系統能否收斂到初始狀態非常重要，不管是系統中每個智能體的初始狀態校準還是智能體狀態需要同步達到初始狀態，這些都需要一種新的系統控制方法。最后，針對無人機編隊中需要初始狀態一致這一場合，分析了本文研究成果的有效性。

2 預備知識及問題描述

2.1 預備知識

2.1.1 代數圖論知識

令G=(v，ξ，A)為一個n階(n≥2)賦權有向圖，其中v={v1，v2，…，vn}為非空節點集合，ξ?v×v為邊的集合，權值鄰接矩陣A=[aij]的鄰接元素aij為非負值。節點指標屬于一個有限指標集Γ={1，2，…，n}。G的邊用eij=(vi，vj)表示。與圖的邊對應的鄰接元素為正，例如，eij∈ξ?aij＞0。另外，假定對所有的i∈Γ，aii=0。節點vi的鄰集由Ni={vj∈v:(vi，vj)∈ξ}表示。集合Ni中元素的數目稱為節點vi的出度，，用矩陣D表示出度矩陣。類似地，集合N～i={vj∈v:(vi，vj)∈ξ}中元素的數目稱為節點vi的入度，由degin表示。令xi∈R表示節點vi的值，將拓撲（或信息流）為G，狀態值為x∈Rn的網絡（或代數圖）表示為Gx=(G，x)。

2.1.2 一致性協議

假定所考慮的動態智能體網絡包含n個智能體。每個智能體被視為有向圖G中的一個節點。每條邊(vj，vi)∈ξ(G(t))對應在時刻t，智能體i到智能體j之間的可靠信息傳遞。另外，每個智能體只根據自身和它鄰居智能體的信息改變目前的狀態值。考慮單積分器智能體動力學特性，令

其中xi(t)∈R為智能體的信息狀態值，ui(t)為時刻t時的控制輸入（或協議）。

2.2 問題描述

多個相互通信的智能體系統，每個智能體只能獲得其鄰居智能體的狀態值，可以用有向圖G=(v，ξ，A)來描述，多智能體的狀態方程可由式（1）表示：

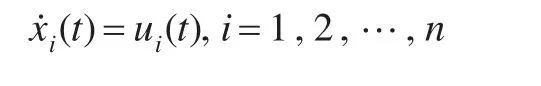
例如，無人機編隊飛行過程中，機群整體協調才能完成它們所承擔的共同任務，必須具有相同的初始姿態，由于某些偶然因素干擾，致使無人機編隊中的各個智能體偏離初始姿態，無法繼續執行既定任務。所以，每個無人機（都是一個智能體）都需要調正自己的姿態至初始設定的姿態值，如果每個智能體都只是孤立地調整自己的姿態，而沒有顧及機群整體的狀態值，一旦自己的姿態調整好之后就去執行整體的任務，而鄰居智能體還沒調整好，任務顯然會失敗。那如何設計一種協議，使得每個無人機都能服從機群整體的狀態改變，即當無人機群中每個無人機（智能體）都調整到初始姿態時才一起執行任務，而某一無人機提前回歸到初始姿態，其他無人機還未準備好時，會繼續使自身處于姿態調整的過程中，不會去執行任務。為解決類似的初始狀態一致問題考慮，針對多智能體系統（1），本文分別從不含時滯和含有時滯兩種情況展開了此類問題的研究。

2.2.1 多智能體系統不含時滯

在多智能體系統不含時滯的情況下，為使多智能體系統收斂到初始狀態量，采用以下一致性控制協議：

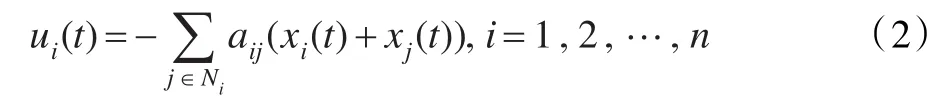
將式（2）代入式（1）可得：

x˙(t)=-(D+A)x(t)（3）其中，x=[x1，x1，…，xn]T，D為出度矩陣，A為臨界矩陣。

2.2.2 多智能體系統含有時滯

在多智能體系統含有時滯的情況下，在式（2）所表示的協議基礎上增加時滯部分，則

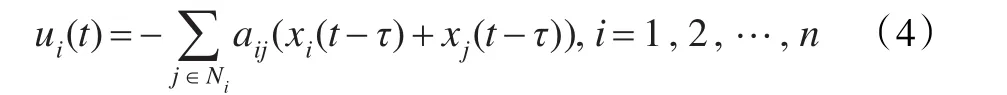
其中，0＜τ＜d為正在通信的兩個多智能體之間的通信時滯。

將式（4）代入式（1）可得：

其中x=[x1，x1，…，xn]T，D為智能體間拓撲結構所對應的出度矩陣，A為對應的鄰接矩陣。

3 主要結論

本章針對多智能體系統（1）在存在時滯和不存在時滯兩種情況下收斂到初始狀態進行分析。為了便于定理推導，先給出一個引理。

引理1[11]給定任意實可微向量函數x(t)∈Rn，任意可微標量函數τ(t)∈(0，h]和任意常矩陣0＜Q=QT∈Rn×n，如下不等式成立：

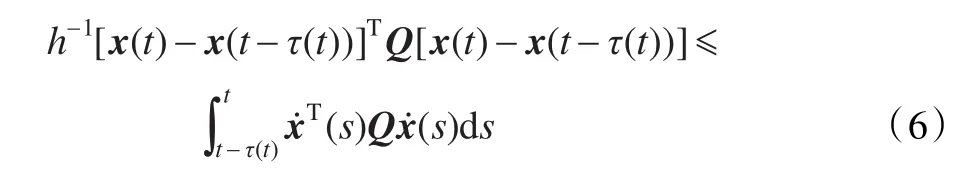
其中，h∈R為正實數，t≥0。

3.1 無時滯情況

定理1如果存在一個對稱矩陣P∈Rn×n，使得

那么由式（3）所確定的一致性協議能使多智能體一致收斂到初始狀態。

證明針對式（1）確定的多智能體系統，構造如下Lyapunov-K rasovskii泛函：

其中，0＜P=PT∈Rn×n。

那么V(t)對時間t求導可得：

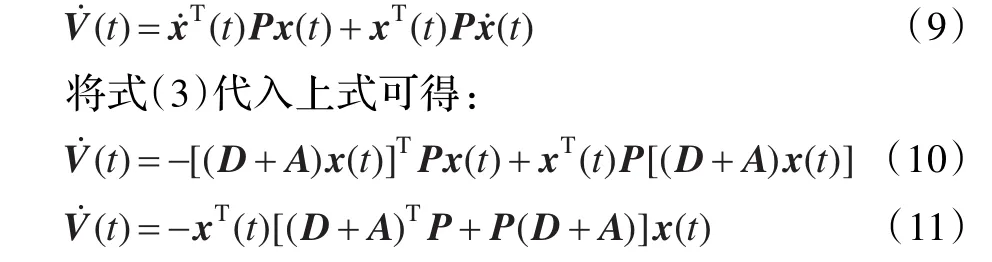
根據式（7）中，(D+A)TP+P(D+A)＞0，所以(t)＜0。由此可得，在滿足式（7）的充分性條件下，由式（3）確定的多智能體系統可達到初始狀態一致。

3.2 時滯情況

定理2假設一階固定時滯多智能體系統滿足以下條件：

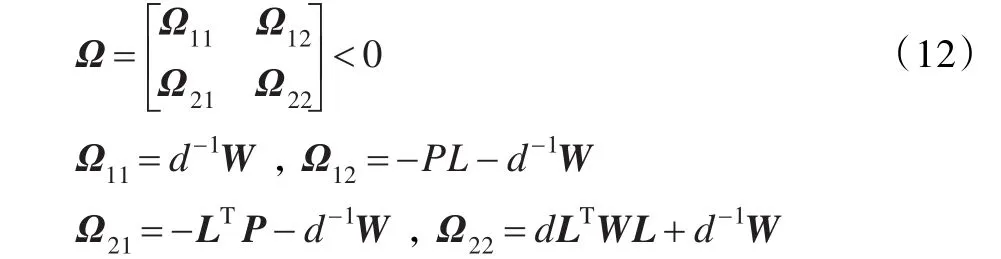
其中，0＜τ＜d，L=D+A，P=PT＞0，W=WT＞0都是適維的矩陣，那么由式（5）決定的多智能體系統收斂到初始狀態0。

證明對于由式（5）確定的多智能體系統，構造如下Lyapunov泛函：

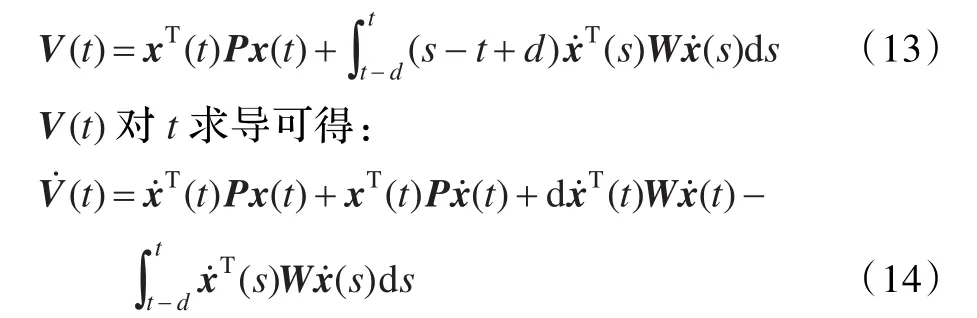
將式（5）代入可得：

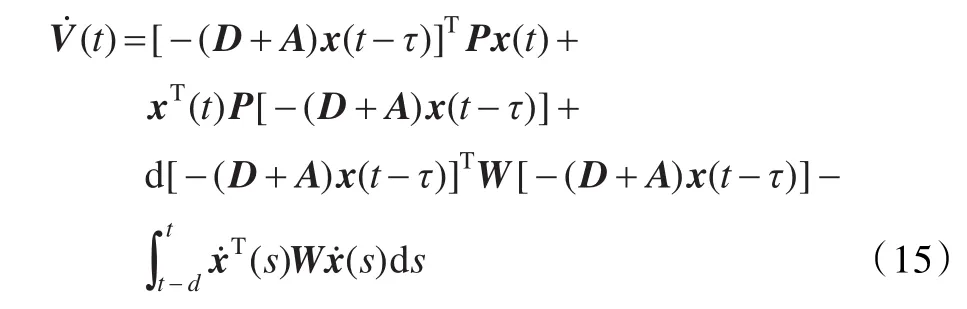
由引理1可推導出：

V˙(t)≤[-(D+A)x(t-τ)]TPx(t)+

xT(t)P[-(D+A)x(t-τ)]+

d[-(D+A)x(t-τ)]TW[-(D+A)x(t-τ)]-

d-1[x(t)-x(t-τ)]TW[x(t)-x(t-τ)]（16）

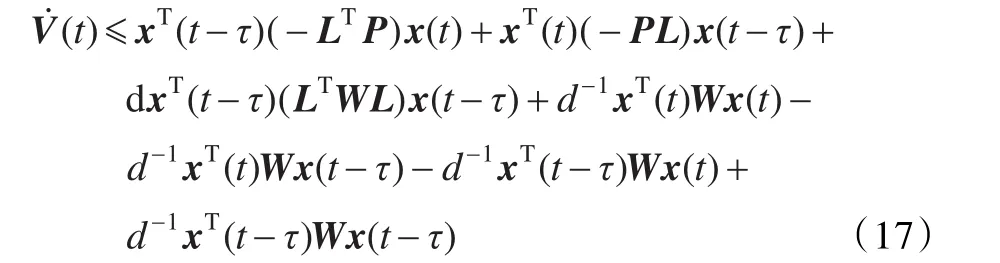
令yT(t)=[xT(t)xT(t-τ)]，則上式可化簡為：

4 仿真及驗證

這里給出計算機仿真實例來驗證上述定理的正確性。

例1考慮如下多智能體系統：

其中xi∈R是第i個智能體的狀態，ui∈R是第i個智能體的控制規則，x(0)i是第i個智能體偏離初始狀態后的當前狀態值，i=1，2，…，5。系統所對應的拓撲結構如圖1所示。

設智能體之間信號傳輸沒有時滯，選取如下各智能體當前狀態值：

x1(0)=6，x2(0)=3，x3(0)=1，x4(0)=-4，x5(0)=-5

由拓撲結構可以得到鄰接矩陣A為：

出度矩陣D=diag(1，1，1，1，1)。

根據是否含有時滯分兩種情況進行討論。

4.1 不含時滯即τ=0的情況

首先根據定理1的公式驗證此種拓撲結構的矩陣表達式是否滿足條件，利用M atlab的LM I工具箱很容易得出一個滿足條件的對稱矩陣P為：

相應的各智能體狀態仿真結果如圖2所示。

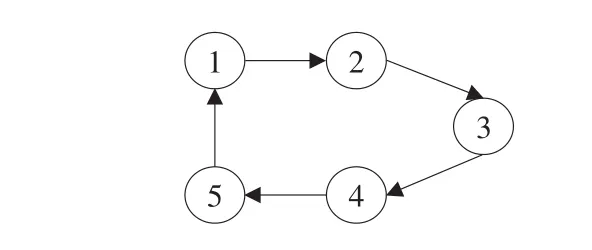
圖1 五個智能體構成的拓撲結構

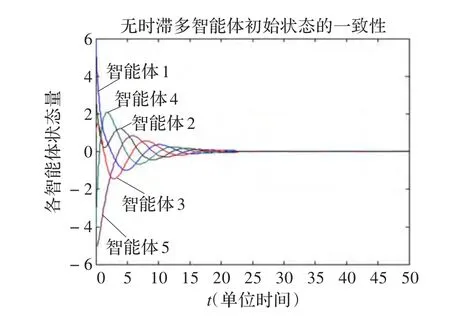
圖2 τ=0時多智能體狀態曲線

通過上述仿真可以得到，使用由式（2）確定的一致性協議，在滿足定理1的情況下，某一個智能體在提前收斂到初始狀態而其他智能體尚未調整到初始狀態值時會繼續使自己處于調整狀態的過程中，最后每個智能體一起達到初始狀態，解決了本文第2章提出的問題。

4.2 含有時滯即0＜τ＜d的情況

在仿真過上述多智能體系統不含時滯的基礎上，本文繼而討論含有時滯τ的情形，此時的d需要滿足一定的條件，不能很大，因為延時量τ的取值范圍不是本文的研究范疇，所以在此為方便仿真取τ為一個比較小的量0.25，在上述拓撲結構和一致性協議下，引入延時量，針對上述假設，進行仿真。仿真結果如圖3所示。

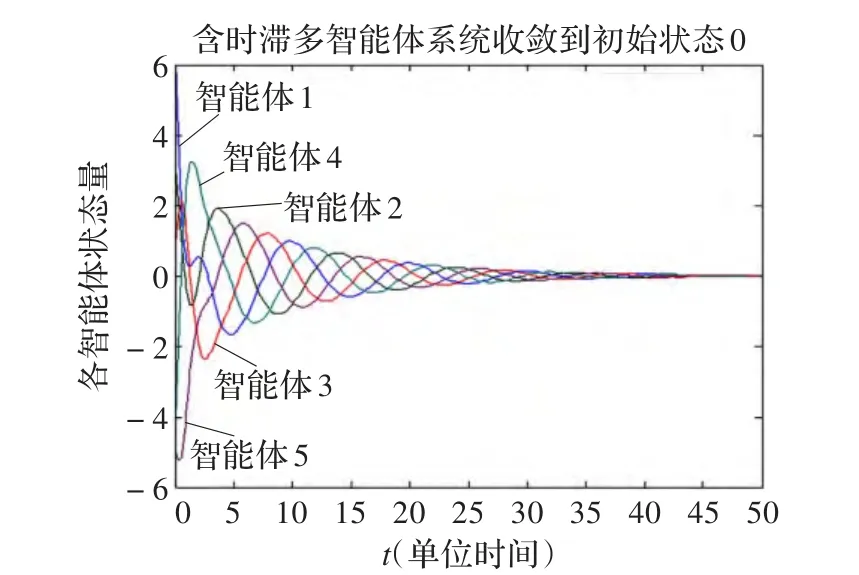
圖3 τ=0.25時多智能體狀態曲線

通過上述仿真可得到，經過一定量的時延之后，收斂速度會變慢，在滿足定理2的條件下，多智能體系統仿真結果與不含時滯的情形相同，一同達到了初始狀態量，驗證了一致性協議及充分性定理的有效性。

5 結束語

研究了多智能體系統收斂到初始狀態的一致性問題，在給出一致性控制協議和定理推導的同時，進行了計算機仿真。解決了無人機編隊飛行中很常見的一個初始狀態一致問題，使得無人機系統在這一局部控制協議下，只通過獲知鄰居無人機的狀態值就可以同步達到初始狀態一致。

本文的研究成果還處于初步階段，今后還將在考慮不同通信時滯，切換拓撲結構的基礎上研究多智能體系統的初始狀態一致性。

[1]Vicsek T，Czirok A，Jacob E B，et al.Novel type of phase transitions in a system of self-driven particles[J].Physics Review Letters，1995，75（6）：1226-1229.

[2]Jadbabaie A，Lin J，Morse A S.Coordination of group of mobile autonomous agents using nearest neighbor rules[J].IEEE Transactions on Automatic Control，2003，48（6）：988-1001.

[3]Ren W，Beard R W.Consensus seeking in multi-agent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control，2005，50（5）：655-660.

[4]M oreau L.Stability of multi-agent system s with time dependent communication links[J].IEEE Transactions on Automatic Control，2005，50（2）：169-182.

[5]Hong Y，Gao L，Cheng D，et al.Lyapunov-based approach to multiagent systems with swithing jointly connected interconnection[J].IEEE Trans on Autom Control，2007，52（5）：943-948.

[6]Yu J Y，Wang L.Group consensus of multi-agent systems with directed information exchange[J].International Journal of Systems Science，2012，43（2）：334-348.

[7]Wang Y Z，Zhang C H，Liu Z B.A matrix apprach to graph maximum stable set and coloring problems with application to multi-agent systems[J].Automatica，2012，48（7）：1227-1236.

[8]Xia W G，Cao M.Clustering in diffusively coupled networks[J].Automatica，2011，47（11）：2395-2405.

[9]Yu J Y，Wang L.Group consensus of multi-agent systems with undirected communication graphs[C]//Proceedings of Asian Control Conference，Beijing，2009：105-110.

[10]Olfati-Sabet R，Murray R M.Consensus problem in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control，2004，49（9）：1520-1533.

[11]Sun Y，Wang L，Xie G.Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays[J].System and Control Letters，2008，57（2）：175-183.