基于改進隨機移動算子的人工魚群算法

淦艷，魏延，，楊有，萬輝

1.重慶師范大學計算機與信息科學學院，重慶401331

2.重慶師范大學科研處，重慶401331

1 引言

生活中許多實際工程問題都可以歸結為一個優化問題，為了尋找該優化問題的最優解，李曉磊等人于2002年提出一種自下而上的新型尋優方法——人工魚群算法（Artificial Fish Swarm Algorithm，AFSA）[1-2]。在文獻[1-2]中李曉磊等給出了人工魚群覓食行為、聚群行為、追尾行為和隨機行為的描述和具體實現。其算法的主要特點是通過比較和移動來實現尋優，易于實現和理解。

但是，使用人工魚群算法在求解多峰函數優化（Multi-peaks Function Optimization）[3]時，存在求解精度有限，運行時間較長，算法易陷入局部最優，魯棒性較差，以及收斂速率較慢和搜索效率不理想的缺點，有許多學者提出了改進算法。其中，針對計算精度不高的缺點，文獻[4]引入模擬退火算法改進人工魚群算法（Simulated Annealing AFSA，SA-AFSA）；文獻[5]采用特殊覓食行為和約束擁擠度區間的方法改進人工魚群算法，文獻[6]采用混合人工魚群算法提高求解精度；文獻[7]引入混沌搜索的思想改進人工魚群算法，均取得了一定的成果。在綜合考慮計算精度和收斂速率問題方面，文獻[8]融合進化策略和粒子群算法改進人工魚群算法；文獻[9]也利用粒子群算法改進人工魚群算法；文獻[10]引入多父體雜交進化技術；文獻[11]提出基于高斯變異算子與差分進化變異算子相結合的混合變異算子的人工魚群算法；文獻[12]針對0/1背包問題，采用隨機鍵的方法以及單位價值啟發式信息進行編碼，直接在編碼空間上進行求解，均提高了計算精度和收斂速率。在綜合考慮計算精度、收斂速率和算法穩定性問題方面，文獻[13]采用保留最優個體，根據雙射的定義和性質，對問題的搜索域進行縮小，加速全局搜索；文獻[14]利用優先適合啟發算法去計算適應度函數值，從實驗結果來看，比AFSA算法有所改進；文獻[15]比較全面地總結了人工魚群算法的改進算法，以及應用領域，并且指出算法存在時間復雜性高，缺乏平衡全局最優和局部最優的缺點。

目前，很少有研究綜合考慮計算精度、魯棒性以及收斂速率和搜索效率問題，只是考慮了其中的部分問題。基于此，本文受到文獻[1-4，8-9，14-16]的啟發，綜合考慮AFSA算法計算精度、魯棒性以及收斂速率和搜索效率問題，提出基于粒子群算法的人工魚群算法（Particle Swarm Optimization AFSA，PSO-AFSA）和包含自適應擾動項的改進人工魚群算法（Adaptive Disturbance Improved AFSA，ADI-AFSA）。對于PSO-AFSA算法主要是利用粒子群算法[3，8-9，16]改進聚群和追尾行為中的隨機移動算子，以概率e-r改進覓食行為[4]中隨機移動算子；對于ADI-AFSA算法主要是對覓食、聚群和追尾行為中隨機移動算子進行改進，添加一項擾動，讓它跳出局部最優值，從而進一步搜索到全局最優值；并從理論上證明了PSO-AFSA和ADI-AFSA算法的收斂性。通過實驗仿真，驗證了本文算法的有效性，避免在尋優時陷入局部最優，提高了AFSA在求解多峰函數最優值時的計算精度，同時驗證了所提出算法比人工魚群算法具有更好的魯棒性，加快了收斂速率和提高了搜索效率。

2 人工魚群基本算法

人工魚群算法（AFSA）是一種新的群智能算法，主要是通過模仿魚的覓食、聚群、追尾和隨機行為來實現尋優的目的。為了更方便描述人工魚群算法，假設：N表表示人工魚個體i、j之間的距離；try_number表示覓食行為試探的最大次數；max gen表示最大迭代次數，gen表示當前迭代次數。如沒有特殊說明，此假設適用于整篇文章。AFSA算法主要包括：覓食、聚群、追尾和隨機行為，其基本思想如下描述。

覓食行為（AF-prey）[1-2，15，17-18]：設人工魚i當前狀態為Xi，在其感知范圍內隨機選擇一個狀態Xj，如果Yi＜Yj（認為后者比前者更優），則向該方向前進一步示人工魚群個體數目；Xi表示人工魚個體的狀態位置，用向量Xi=(x1，x2，…，xn)表示，其中xi(i=1，2，…，n)是尋優的變量；Yi表示第i條人工魚當前所在位置的食物濃度，用Yi=f(Xi)表示目標函數；Visual表示人工魚的感知距離；Step表示人工魚移動的步長；δ表示擁擠度因子；，反之，再重新隨機選擇狀態Xj，判斷是否滿足前進條件，并反復嘗試try_number次，若仍不滿足前進條件，則隨機移動一步

聚群行為（AF-swarm）[1-2，15，17-18]：設人工魚i當前狀態為Xi，探索當前鄰域內(di，j＜Visual)的伙伴數目nf及中心位置Xc。若Yc/nf＞δYi，表明伙伴中心有較多食物且不太擁擠，則朝伙伴的中心位置方向前進一步，否則執行覓食行為。

追尾行為（AF-follow）[1-2，15，17-18]：是一種向鄰近的有著最高適應度的人工魚追逐的行為，在尋優算法中可以理解為是向附近的最優伙伴前進的過程。設人工魚i當前狀態為Xi，探索當前鄰域內(di，j＜Visual)的伙伴中Yj為最大值的伙伴Xj，若Yj/nf＞δYi，表明伙伴Xj的狀態具有較高的食物濃度并且其周圍不太擁擠，則朝Xj的方向前進一步，否則執行覓食行為。

隨機行為（AF-move）[1-2，15，17-18]：隨機行為就是在視野中隨機選擇一個狀態，然后向該方向移動，其實是覓食行為的一個缺省值。

從AFSA算法的行為描述可知，在覓食行為、聚群行為和追尾行為中均出現隨機移動的情況，會降低算法的收斂速率。針對收斂速率不樂觀的問題，文獻[18]提出了對覓食行為、聚群行為和追尾行為進行改進的策略，主要是限制隨機移動的范圍于定義區間內，讓它在事先定義的區間內移動，這樣可以加快收斂速率。實驗仿真表明，可以提高計算的精度。為了后面表述方便，稱其為限制隨機移動的人工魚群算法（Limited Move AFSA，LM-AFSA）。為了便于說明將文獻[4]中SA-AFSA和文獻[18]中LM-AFSA算法視為傳統改進算法。

3 基于粒子群算法的人工魚群算法

針對人工魚群算法優化精度不足、魯棒性較差，以及收斂速率較慢和搜索效率較低的缺點，受文獻[3，8-9，16]的啟發，本文提出了基于粒子群算法的人工魚群算法（PSO-AFSA）。

3.1 PSO-AFSA算法思想

PSO-AFSA算法主要思想是利用粒子群算法改進聚群和追尾行為中的隨機移動算子，改進的聚群行為隨機移動算子描述如下：

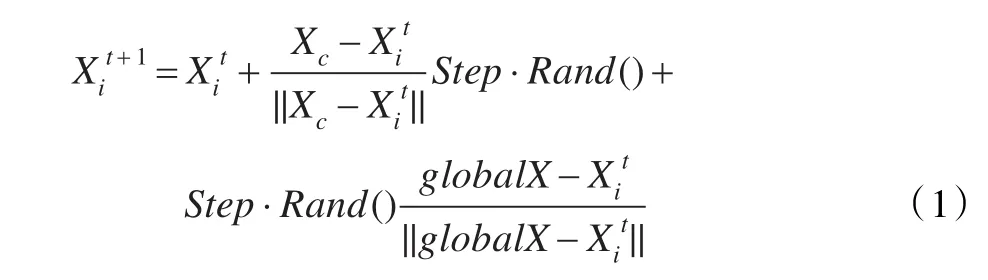
其中，Xc是中心位置，Rand()是0到1之間的隨機數，globalX是全局的最優值，下同。改進的追尾行為隨機移動算子描述如下：

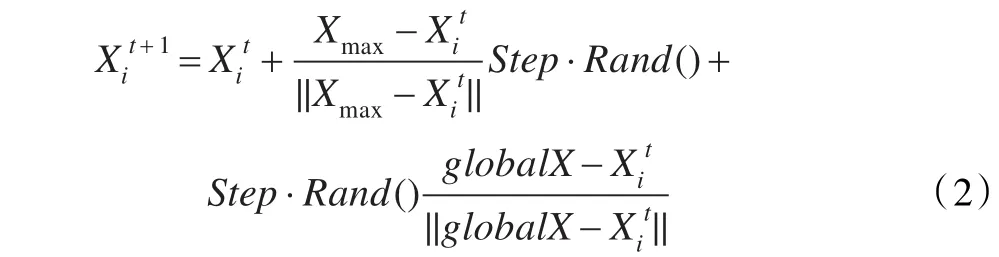
其中，Xmax是探索其視野范圍內最優的一個值。其次，就是以概率e-r改進覓食行為[4]中隨機移動算子，其中r=i/max gen，即滿足概率e-r，就執行覓食行為的隨機移動算子，其描述如下：

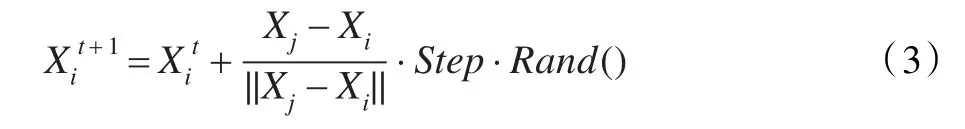
如果不滿足概率e-r，則直接移動到Xj，即并且限制覓食、聚群和追尾行為中向前移動一步的范圍，具體做法是：當時，取；當時，取=Xmin；這樣就在定義區間[Xmin，Xmax]內。另外采用公告牌用來記錄最優人工魚個體狀態，每條人工魚在每次尋優過程完成后，自動與公告牌的狀態相比，如果自身狀態優于公告牌狀態，就將公告牌狀態替換為自身狀態，這樣公告牌就記錄了最優的人工魚狀態。

3.2 PSO-AFSA算法描述

首先初始化參數，然后執行聚群行為、覓食行為、追尾行為和隨機行為，采用公告牌記錄最優值，詳細的描述見算法1。

算法1基于粒子群算法的人工魚群算法（PSO-AFSA算法）

步驟1初始化人工魚群中參數和公告牌信息，即：N、Visual、try_number、δ、max gen、gen=1、BestY、BestX；公告牌中參數：besty、bestx。

步驟2 執行聚群行為、覓食行為、追尾行為和隨機行為，具體在執行聚群、追尾和覓食行為中的隨機移動算子時，分別按照式（1）、（2）和（3）所給的移動算子執行。

步驟3 每條人工魚每完成一次尋優，BestY就與besty比較，若BestY優于besty，首先用BestY去更新besty，同時將記錄besty所對應的bestx，然后轉步驟4；反之，若BestY沒有besty優，不用更新，直接轉步驟4。

步驟4判斷是否滿足結束條件gen≤max gen，若滿足，則返回到步驟2繼續執行；反之，若不滿足gen≤max gen，則轉步驟5。

步驟5 算法結束。結束時，besty中即為所求函數最優值，而bestx中記錄的就是besty所對應的自變量值。

算法1中的聚群和追尾行為隨機移動算子采用了粒子群算法的思想進行改進，利用粒子群算法有顯著的全局搜索能力優點，能夠使得算法1跳出局部最優，進而求得最優問題的全局最優值；采用以概率e-r改進覓食行為隨機移動算子，提高了算法1的計算精度；采用限制隨機移動范圍于定義區間的方法，能夠提高算法1的收斂速率。采用粒子群算法思想，以概率移動的思想和限制移動范圍相結合方式改進隨機移動算子，加快了算法1收斂速率，提高了魯棒性以及求解的計算精度。

4 包含自適應擾動項的改進人工魚群算法

在AFSA算法中的覓食、聚群和追尾行為中，均出現隨機移動一步的現象，它會使得算法陷入局部最優，降低收斂效率和搜索效率。為了克服AFSA算法的缺點，本文提出了包含自適應擾動項的改進人工魚群算法（ADI-AFSA）。

4.1 ADI-AFSA算法思想

ADI-AFSA算法主要是對覓食、聚群和追尾行為中隨機移動算子進行改進，具體做法是在覓食、聚群和追尾行為中添加一項擾動，讓它跳出局部最優，進一步搜索到全局最優值，從而達到加快收斂速率和提高搜索效率的目的。改進后覓食行為隨機移動算子描述如下：

改進后的聚群行為隨機移動算子描述如下：

改進后的追尾行為隨機移動算子描述如下：

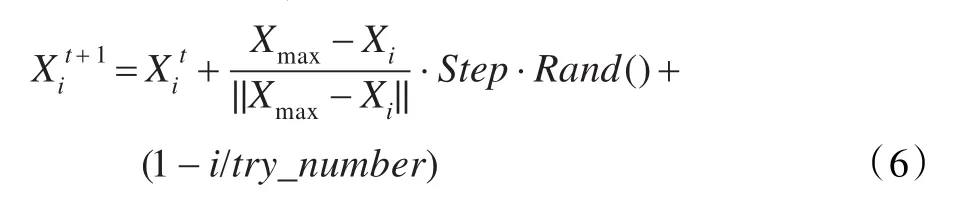
其中，式（4）、（5）和（6）中(1-i/try_number)是擾動項，i是1～1-i/try_number的整數變量，隨著當前第多少次嘗試的改變而改變，因此叫做自適應擾動項；式（5）中Xc是中心位置；式（6）中Xmax是探索其視野范圍內最優的一個值。并且同樣限制覓食、聚群和追尾行為中向前移動一步的范圍，具體的做法：當＞Xmax時，取；當＜Xmin時，取=Xmin；這樣就在定義區間[Xmin，Xmax]內。同理也采用公告牌，用于記錄最優值。

4.2 ADI-AFSA算法描述

首先初始化參數，然后執行聚群行為、覓食行為、追尾行為和隨機行為，同樣采用公告牌策略，詳細的描述見算法2。

算法2 包含自適應擾動項的改進人工魚群算法（ADI-AFSA算法）

步驟1初始化人工魚群中參數和公告牌信息，包括：N、Visual、try_number、δ、max gen、gen=1、BestY、BestX；公告牌中參數：besty、bestx。

步驟2執行聚群行為、覓食行為、追尾行為和隨機行為，具體在執行覓食、聚群和追尾行為中隨機移動算子時，分別按照式（4）、（5）和（6）所給的移動算子執行。

步驟3 每條人工魚每完成一次尋優，BestY就與besty比較，若BestY優于besty，首先用BestY去更新besty，同時將記錄besty所對應的bestx，然后轉步驟4；反之，若BestY沒有besty優，不用更新，直接轉步驟4。

步驟4 判斷是否滿足結束條件gen≤max gen，若滿足，則返回到步驟2繼續執行；反之，若不滿足gen≤max gen，則轉步驟5。

步驟5 算法結束。結束時，besty中即為所求函數最優值，而bestx中記錄的就是besty所對應的自變量值。

算法2中的聚群、覓食和追尾行為隨機移動算子均采用了增加擾動的思想進行改進，能夠使得算法2跳出局部最優，進而求得最優問題的全局最優值；采用限制隨機移動范圍于定義區間的方法，能夠提高算法2的收斂速率。采用帶有擾動和限制移動范圍移動的結合方式改進隨機移動算子，加快了算法2收斂速率和搜索效率，提高了求解的計算精度以及具有較好的魯棒性。

5 PSO-AFSA和ADI-AFSA算法收斂性分析

命題1 當時間趨于無窮時，PSO-AFSA和ADI-AFSA算法具有全局漸近收斂性。

證明因為在PSO-AFSA和ADI-AFSA算法的覓食、聚群和追尾行為中，個體在尋優過程中有信息交換和相互學習的行為，即有“社會協作[19]”；還有個體主動或被動地調節自身的狀態以更好地適應環境，即有“自我適應[19]”；以及使用公告牌策略，即有“競爭[19]”。從PSO-AFSA和ADI-AFSA算法描述中可知，改進的PSO-AFSA和ADIAFSA算法滿足群智能算法統一框架中迭代搜索過程中的社會協作、自我適應和競爭3個基本條件，即可以將PSO-AFSA和ADI-AFSA算法歸到智能算法統一框架中，由智能優化統一框架算法性能所列出的收斂性結論[19]可知，當時間趨于無窮，基于統一框架的保優性群體智能優化（Population-based Intelligent Optim ization，PIO）算法具有全局漸近收斂性，即命題1成立。

引理若一個算法滿足如下兩個條件[8，20-21]：

（1）對可行域內的任意兩個點X和X′，X′是X通過進化為η精度可達的；

（2）算法采用的是精英保存策略，即最優個體是單調的，則算法以概率1收斂到具有η精度的全局最優解。

命題2若待求解的優化問題在搜索空間域中連續，則PSO-AFSA和ADI-AFSA算法以概率1收斂到待求解優化問題的全局最優解。

證明因為在PSO-AFSA和ADI-AFSA算法的行為中有“自我適應”，即存在進化的過程，使得PSO-AFSA和ADI-AFSA算法滿足引理條件（1）；在PSO-AFSA和ADIAFSA算法中均采用公告牌的策略，因此所記錄的優化函數值構成的數列是一個單調的數列，從而使得算法中魚群最優個體狀態是單調的，滿足引理條件（2），即命題2得證。

6 仿真實驗

為了驗證所提出的PSO-AFSA和ADI-AFSA算法的計算精度、魯棒性、收斂速率以及搜索效率的優越性，下面將具體介紹測試函數及參數的選取和實驗結果分析。

6.1 測試函數及參數的選取

為了驗證提出的基于粒子群算法的人工魚群算法（PSO-AFSA）和包含自適應擾動項的改進人工魚群算法（ADI-AFSA）的性能，本文采用文獻[17]附錄B中所提供的公認測試函數集，因在求解最大值與最小值之間可以添加符號相互轉化，所以本文選取了其中的5個求最大值的多峰函數進行測試。具體所選取的測試函數如下：

（2）max F2(x，y)=x sin(4πx)-y sin(4πy+π+1)，x,y∈[-1，2]。max F2(1.628 9，2)=3.309 9，即在點（1.628 9，2）處，F2取得全局最大值3.309 9。

（3）max F3(x，y)=cos(2πx)×cos(2πy)×e-(x2+y2)/10，x，y∈[-1，1]，max F3(0，0)=1，即在點（0，0）處，F3取得全局最大值1。

運行環境：處理器Intel?CoreTMi3-2350M CPU@2.30 GHz，內存為4.00 GB，MATLAB版本為matlabR2012b。對于測試函數F1、F2、F3、F4和F5所選用的人工魚群算法參數受到文獻[8，13，18]的啟發并通過大量的對比實驗分析，所選參數的具體值如表1所示。

表1 人工魚群算法參數設置

6.2 實驗結果分析

根據表1設置的參數，以及考慮到對比性，針對測試函數F1、F2、F3、F4和F5所選用的參數均相同。每種算法對每個測試函數進行20次實驗，記錄下20組實驗值。得出測試函數F1、F2、F3、F4和F5在AFSA、LM-AFSA、SA-AFSA、PSO-AFSA和ADI-AFSA等5種算法的尋優結果，如表2所示。

針對不同的測試函數，相同的測試參數，通過實驗仿真表明：

（1）從表2仿真結果中最佳優化值來看，對于測試函數F1、F2、F3、F4和F5，PSO-AFSA和ADI-AFSA算法得到的結果均比AFSA、LM-AFSA和SA-AFSA算法得到的結果理想，顯示出改進算法的明顯優勢。其次從最差優化值和平均優化值來看，改進算法得到的結果在不同測試函數下，也顯示出一定優勢。另外，對于同一測試函數F1來說，改進算法得到的最佳優化值1.000 00比文獻[5]中給出的全局最優值0.999 20要精確，已達到理論的分析值。對于測試函數F2來說，算法得到的最佳優化值3.309 89更接近文獻[17]給出的函數全局最優值3.309 90。對于測試函數F3和F4來說，改進算法得到的最佳優化值更接近文獻[17]中給出的全局最優值1.000 00。對于測試函數F5來說，改進算法得到的最優值更接近文獻[17]中給出的全局最優值186.730 91。這些結果說明改進算法具有更高的計算精度，能夠搜索到全局最優值。

（2）對于測試函數F1、F2、F4和F5，與其他4種算法相比，PSO-AFSA算法所得到的優化值方差更小，說明改進的PSO-AFSA算法具有更好的魯棒性。在測試函數F1和F5中，ADI-AFSA算法所得到的優化值方差比AFSA、LM-AFSA和SA-AFSA算法要小，表明ADI-AFSA算法也表現出較好魯棒性的優點。

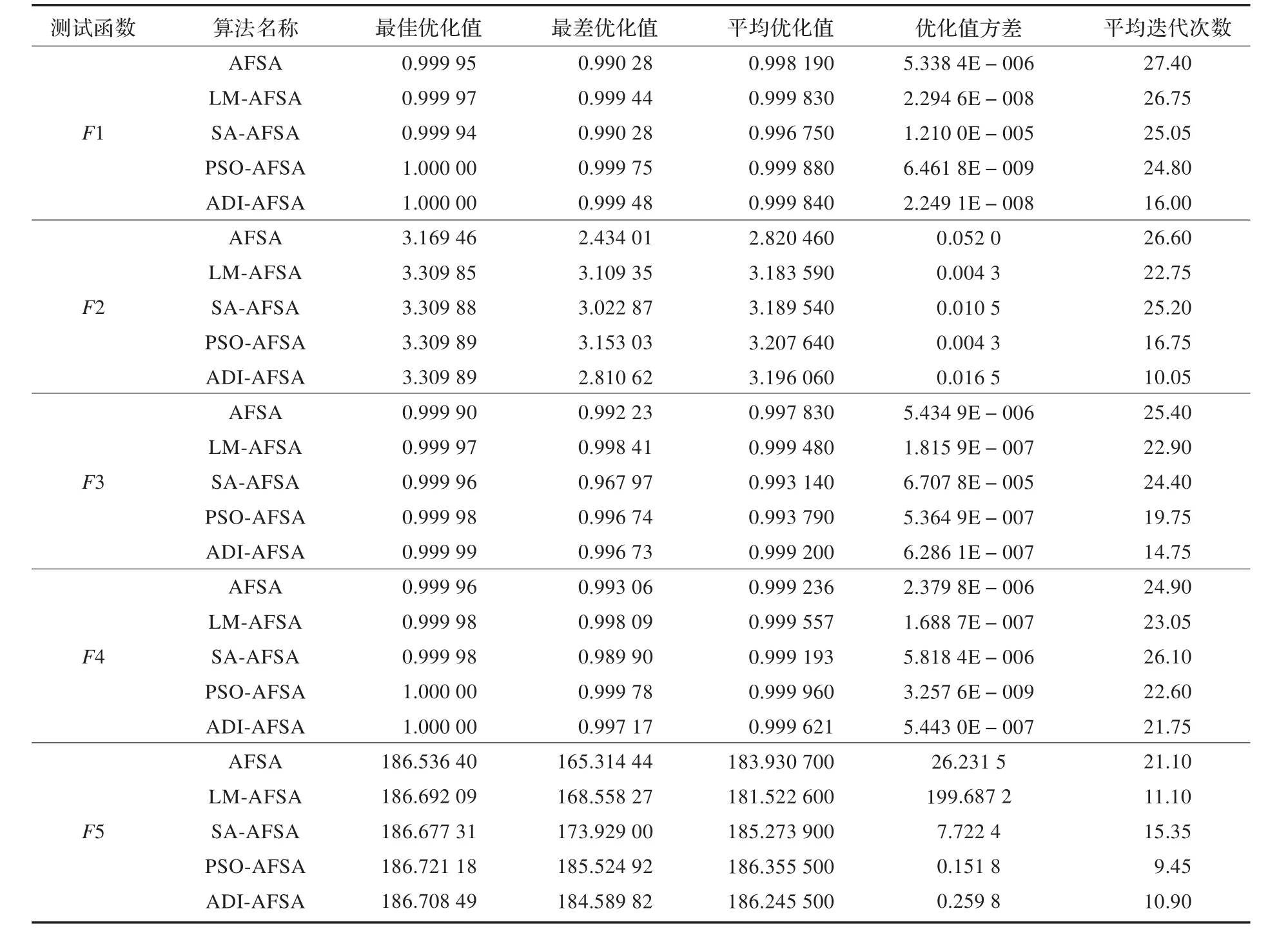
表2 仿真結果

（3）對于測試函數F1、F2、F3、F4和F5，改進的PSO-AFSA和ADI-AFSA算法的平均迭代次數小于AFSA、LM-AFSA和SA-AFSA算法的平均迭代次數，說明改進的PSO-AFSA和ADI-AFSA算法具有更好的收斂速率和搜索效率。

7 結束語

針對人工魚群算法在求解多峰函數優化問題時，搜索全局最優解的能力不足，求解精度不夠，魯棒性較差以及收斂速率較慢和搜索效率較低的缺點，提出基于粒子群算法的人工魚群算法（PSO-AFSA）和包含自適應擾動項的改進人工魚群算法（ADI-AFSA）兩種算法，主要是以概率隨機移動的思想改進覓食行為中隨機移動算子，利用粒子群算法的思想去改進聚群行為和追尾行為中的隨機移動算子，以及利用擾動項的思想改進覓食行為、聚群行為和追尾行為中隨機移動算子。并且嚴格限制隨機移動算子在定義區間[Xmin，Xmax]內，最后利用公告牌記錄全局的最優值，并從理論上分析了兩種改進算法的收斂性。通過對5個典型的多峰函數進行實驗仿真，結果表明改進隨機移動算子能夠進一步提高求解多峰函數最優值的求解精度，克服了人工魚群算法求解精度不足和搜索全局最優值能力有限的缺點。而且改進了的隨機移動算子使得提出的算法與人工魚群算法及傳統算法相比，具有更好的魯棒性，以及更好的收斂速率和搜索效率。

[1]李曉磊，邵之江，錢積新.一種基于動物自治體的尋優模式：魚群算法[J].系統工程理論與實踐，2002，22（11）：32-38.

[2]李曉磊.一種新型的智能優化方法——人工魚群算法[D].杭州：浙江大學，2003.

[3]趙吉，孫俊，須文波.一種求解多峰函數優化問題的量子行為粒子群算法[J].計算機應用，2006，26（12）：2956-2960.

[4]劉佳，劉麗娜，李靖，等.基于模擬退火算法的改進人工魚群算法研究[J].計算機仿真，2011，28（10）：195-198.

[5]張嚴，楚曉麗.一種改進的人工魚群算法[J].計算機系統應用，2011，20（5）：199-201.

[6]鄧濤，姚宏，杜軍.多峰函數優化的改進人工魚群混合算法[J].計算機應用，2012，32（10）：2904-2906.

[7]Chen Z H，Tian X Q.Artificial fish-swarm algorithm with chaos and its application[C]//Proceedings of the 2nd International Workshop on Education Technology and Computer Science，2010：226-229.

[8]曲良東，何登旭，黃勇.一種新型的啟發式人工魚群算法[J].計算機工程，2011，37（17）：140-142.

[9]范玉軍，王冬冬，孫明明.改進的人工魚群算法[J].重慶師范大學學報：自然科學版，2007，24（3）：23-26.

[10]Luo Y X.The novel compound evolutionary optimization algorithm with hybrid discrete variables and its application to mechanical optimization[J].Advaned Macterials Research，2010（97/101）：3276-3280.

[11]曲良東，何登旭.混合變異算子的人工魚群算法[J].計算機工程與應用，2008，44（35）：50-52.

[12]厙向陽，朱命昊，趙亞敏.求解0/1背包問題的改進人工魚群算法研究[J].計算機工程與應用，2011，47（21）：43-46.

[13]姚祥光，周永權，李詠梅.人工魚群與微粒群混合優化算法[J].計算機應用研究，2010，27（6）：2084-2086.

[14]Zheng Genrang，Lin Zhengchun.A w inner determination algorithm for combinatorial auctions based on hybrid artificial fish swarm algorithm[J].Physics Procedia，2012，25：1666-1670.

[15]Neshat M，Sepidnam G，Sargolzaei M，et al.Artificial fish swarm algorithm：a survey of the state-of-the-art，hybridization，combinatorial and indicative applications[J/OL].（2012-05）[2013-12-31].http：//dx.doi.org/10.1007/s10462-012-9342-2.

[16]Zhan Zhihui，Zhang Jun，Chung H S H.Adaptive particle swarm optimization[J].IEEE Transactions on Systems，M an，and Cybernetics，2009，39（6）：1362-1381.

[17]江銘炎，袁東風.人工魚群算法及其應用[M].北京：科學出版社，2012.

[18]史峰，王輝，郁磊，等.MATLAB智能算法30個案例分析[M].北京：北京航空航天大學出版社，2011.

[19]王凌，劉波.微粒群優化與調度算法[M].北京：清華大學出版社，2008.

[20]Back T.Evolutionary algorithms in theory and practice[M].New York：Oxford University Press，1996.

[21]劉淳安，王宇平.約束多目標優化問題的進化算法及其收斂性[J].系統工程與電子技術，2007，29（2）：277-280.