基于DOA測量的多目標位置信息場定位精度分析

馬賢同，羅景青

1.電子信息控制重點實驗室，合肥230037

2.電子工程學院，合肥230037

無源定位屬于被動定位，系統具有很好的隱蔽性，不易受到干擾和攻擊，是目前定位研究的主要方向。目前主要的無源定位技術中應用的最廣泛的是：測向交叉定位法[1]和時差定位法[2-3]。很多學者對復合定位法進行了研究，主要包括聯合利用方位角與時間差信息的DT法[4]、聯合利用方位角與多普勒（Doppler）信息的DF法[5]等。

相較于上述定位方法，測向交叉定位法具有全方位、快速、探測距離遠、抗干擾能力強等優點。在實戰中，偵察系統往往在同一時間面對的是空間多個輻射源的復雜電磁環境，有時需要對多個同類輻射源同時進行定位。現有的諸多定位方法都是針對單目標定位的，它們在進行定位計算之前，都要知道測量參數是關于某個確定目標的。文獻[6]直接利用觀測站得到的方位數據，用尋找最大可能密度區域的方法來確定目標的位置，但只研究了一個目標的情況。而位置信息場定位法不需要對測量參數按目標進行分類，同時確定目標數目和目標的位置。例如，對測得的一組方位角數據，不知道這些方位角數據是關于一個目標的還是兩個目標的或者更多目標的，這時可用位置信息場定位法確定目標數目和目標的位置。在此基礎上，對基于DOA信息的位置信息場定位方法進行了精度分析，通過理論推導得到了定位誤差的協方差矩陣，運用橢圓概率誤差與定位誤差幾何分布來描述定位精度。研究結果為該類系統的技術作戰運用提供了理論支持。

1 目標位置信息場定位法原理

定義在指定區域內關于感興趣目標或目標群位置分布的函數，為目標位置信息場函數，簡稱目標位置信息場或位置信息場。目標位置信息場是一個標量場，是關于目標或目標群位置分布特征的一個描述。在二維平面或三維空間甚至更高維空間，關于目標和目標群的本體位置特征可用一個精確位置概率分布密度來表達：

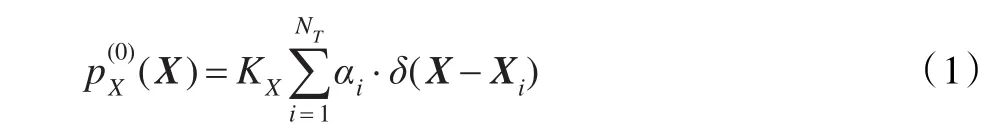
其中，X表示所關心的可能存在目標的位置，NT為目標的個數，αi為在位置Xi存在目標的相對可靠性因子，KX為歸一化系數，而δ(·)為犾拉克函數。

一般，式（1）很難得到，而可以得到的只是式（1）的一個估計。當獲得了一批觀測（信號測量數據或測量參數集）Z后，由于觀測的有限時域特性和有限頻域特性，得到的結果是式（1）與一些函數的卷積：

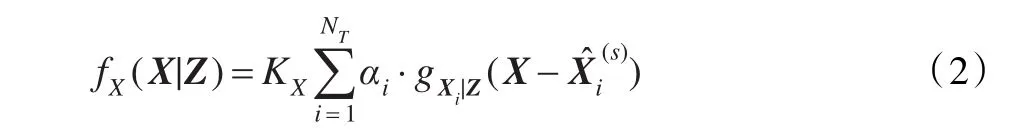
式中，fX(X|Z)就是基于觀測Z的關于目標的位置信息場函數，…，NT為當目標作為單目標時Xi的估計結果，是Z的函數。是某個在X=處取極大值且只有一個極值的實函數。Z實際上是一觀測空間，它可以是任何與目標位置有關的觀測值的集合，可以是多個觀測矢量的組合。之所以給出單目標時的估計結果，是因為在多目標情況，由于各目標后驗概率密度函數的互相影響，其估計結果可能不再具有與式（1）相對應的形式。

需要指出的是，式（1）中的Z可以是多個方位或方位和距離或功率或衰減因子及相關參數，也可以是到達時間、到達時間差、頻差、相位差、相位差變化率、方位變化率等等，當然還可以是直接時域采樣數據[7]、直接頻域采樣數據[8]，甚至可以是位置取樣值本身。根據Z，求得fX(X|Z)，并從中分析出目標的個數、目標的位置的方法，稱之為位置信息場定位法[9]。

2 基于DOA測量的位置信息場定位法

2.1 觀測模型

一般，無論是無源定位，還是有源定位，總是靠多次測量與目標位置有關的參數或信號后，對目標位置進行確定（估計）的。對只測向定位（以方位角為例）而言，P個觀測站所得到的觀測值Z可描述成多個獨立測量的方位角矢量的組合：

其中M≥1，表示獨立觀測的次數。而相應于zm的目標“響應”函數hm(XE)為：

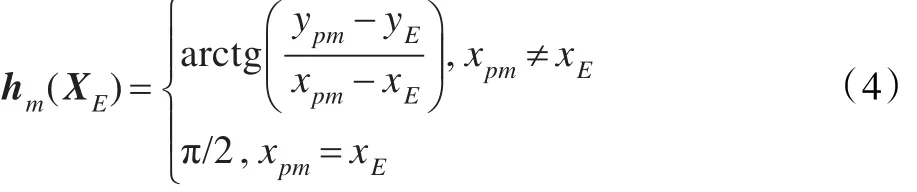
其中，m=1，2，…，M，XE=(xE，yE)為目標位置坐標，XE可能是一個確知參量，也可能是多個確知參量，還可以是隨機參量。對于多目標的情況，它可以是任意一個目標的位置坐標。以兩個目標（用1和2表示）為例，(xE，yE)可能是目標1的坐標，也可能是目標2的坐標。式（4）中(xpm，ypm)，?p=1，2，…，P，為在獲得第m組測量值時觀測站p所對應的位置。一般地，對陣列測向系統而言，方位角定義為陣列法線方向到輻射源波達方向的夾角。假設陣列基線方向與X軸方向一致，如圖1所示。

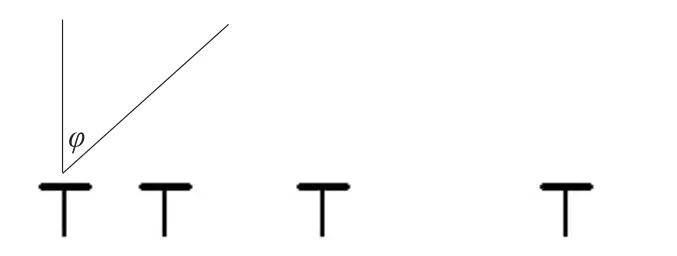
圖1 陣列布局示意圖

每個獨立的觀測量一般均是受測量噪聲污染后的與目標位置有關的函數：

其中，hm(XE)為目標對應于測量zm無噪時的“響應”，其形式由式（4）確定，而vm是觀測量zm的測量誤差，假定測量噪聲是零均值的，其協方差矩陣為：

設XE的先驗概率密度為p0(X)，則可定義目標位置信息場為：

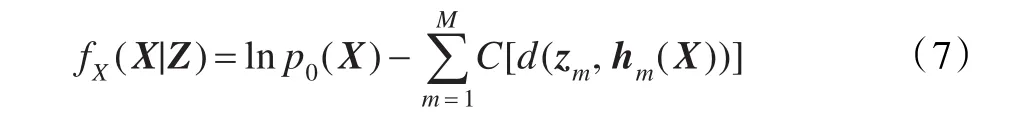
是觀測矢量zm與場內點X處目標響應hm(X)的標稱化距離（歐氏距離）。為一代價函數，而

2.2 代價函數的選取

對可能存在目標的一個感興趣的區域，就某一觀測站而言，區域內的每一點都可以得到相對于該觀測站的一個方位角，這些方位角組成一個集合，用B表示。對于觀測站測得的每一個方位角z而言，z∈B。B中一些方位角是與z離得比較“近”的，一些則離得比較“遠”。在對目標進行定位的過程中，就需要對B中的方位角進行處理，使得與z離得比較“近”的方位角信息對定位結果的“貢獻”大，使與z離得比較“遠”的方位角信息對定位結果的“貢獻”小。

設方位角測量誤差的均值為0，標準差為σθ。對某一觀測站得到的每一個方位角z，式（8）可以寫為：

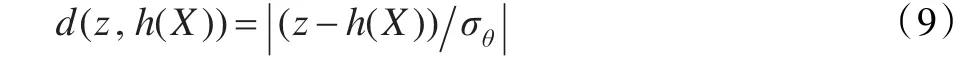
其中||???表示取絕對值，且

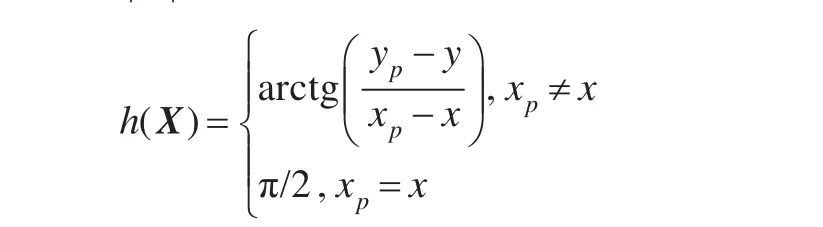
h(X)表示區域X內任意一點(x，y)對應于觀測站(xp，yp)的方位角。則代價函數可以定義如下：

其中，γ為一門限。

由于式（10）代價函數的選取，在一定程度上突出了有價值信息對定位結果的“貢獻”，對不可靠的或者價值小的信息的“貢獻”進行了弱化。

3 基于DOA測量的位置信息場定位精度分析

位置XE的估計是使式（7）最大的估計，結合代價函數，在目標附近區域內，可以推得，使式（7）最大的估計也是使

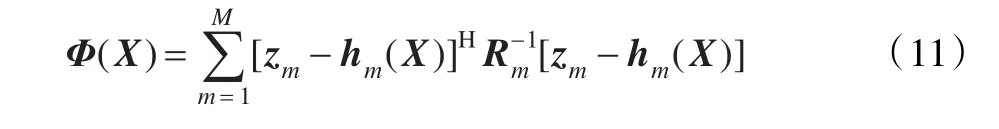
取最小值的估計。

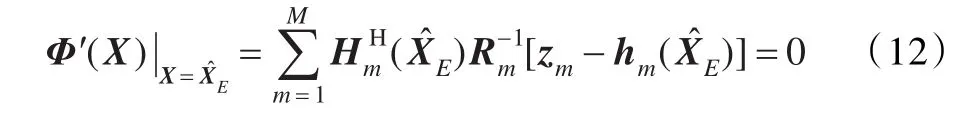
其中，當XE=(xE，yE)T時：

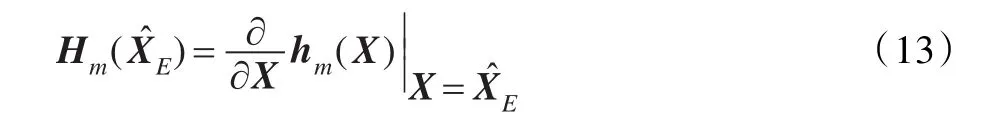
作近似處理：

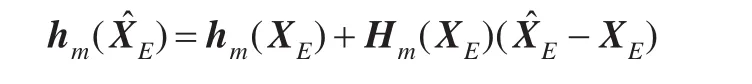
且假定：

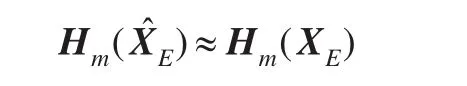
再考慮到zm=hm(XE)+vm，由式（12）可得：

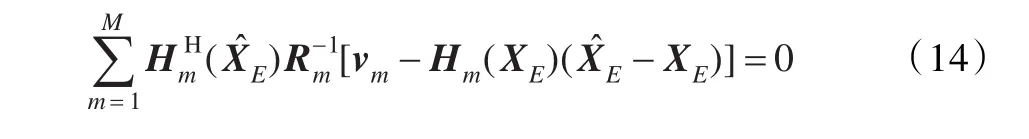
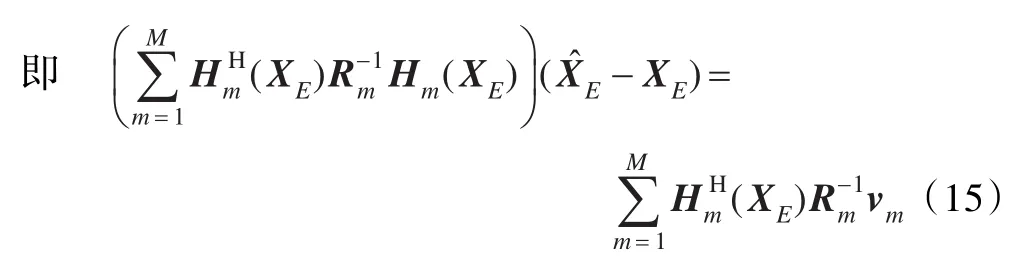
對式（15）兩邊求均值，可得：

對式（15）兩邊求協方差矩陣，可得：

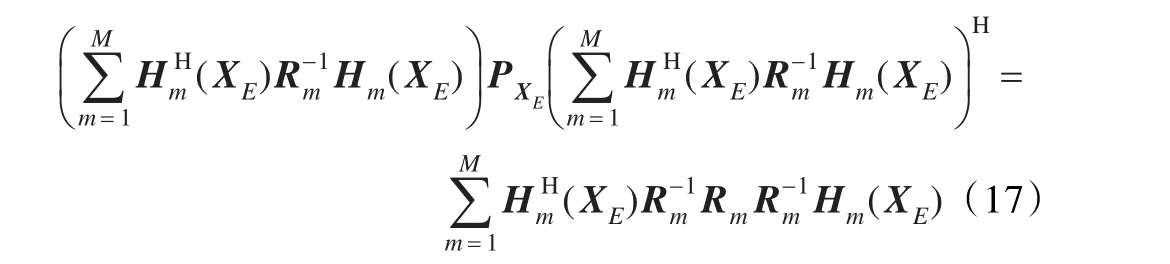
其中PXE為定位誤差協方差矩陣，化簡式（17）可得：

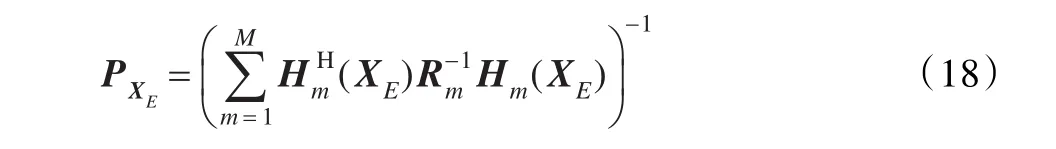
令最終計算得到的定位誤差協方差矩陣為：

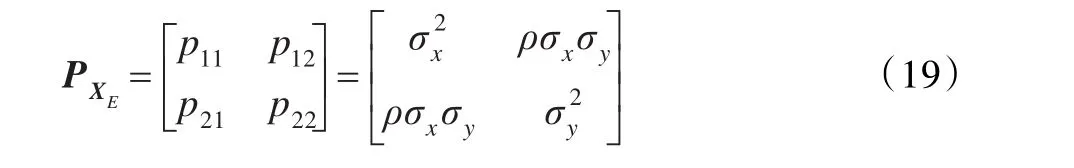
3.1 橢圓概率誤差表示法

根據協方差矩陣PXE，可以確定定位誤差橢圓關于x，?y的方程為：

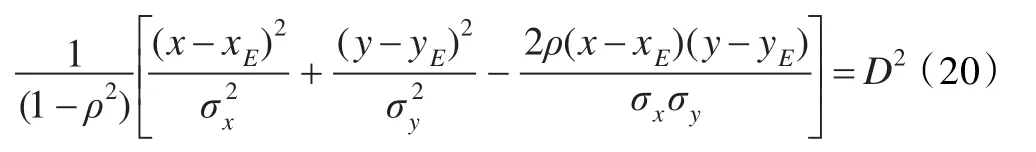
其中，D2=-2 ln(1-P)，通常將P=0.5所對應的橢圓稱為橢圓概率誤差；xE、?yE為目標輻射源坐標值。定位誤差橢圓的半長軸a、半短軸b和長軸方向θ的計算參見文獻[10]。

3.2 定位誤差幾何分布表示法

根據式（19），則定位誤差的幾何分布（Geometric Dilution of Precision，GDOP）可表示為：

根據GDOP分布圖及測向定位原理可以得出，誤差最小的定位方向應位于基線的法線方向，下面的仿真實驗將會驗證這一點。

4 仿真實驗

假設三個觀測站對輻射源進行測向定位，觀測站1的位置為(-30 km，3 km)，得到關于輻射源的方位角為29.8°和47.2°；觀測站2的位置為(0 km，3 km)，得到關于輻射源的方位角為8.3°和27.5°；觀測站3的位置為(30 km，3 km)，得到關于輻射源的方位角為－17.9°和0.5°，稱相鄰兩個觀測站的距離為基線長度，此時基線長度l為30 km。圖2（a）是利用觀測站得到的方位角畫出的測向定位線，其中“o”表示觀測站的位置，圖2（b）是運用位置信息定位的效果圖，可以確定目標的個數為2，目標的位置分別為(9 km，70 km)和(30 km，59 km)。

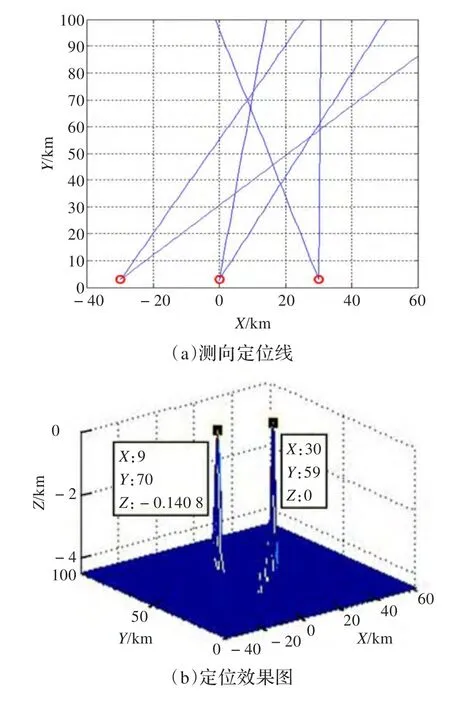
圖2 位置信息場定位

（1）測向精度對定位精度的影響

觀測站的位置同上不變，圖3繪制了測向精度σθ分別為1°和0.5°時的定位精度分布圖。圖3中（a）采用橢圓概率誤差表示法，（b）采用定位誤差幾何分布表示法，分別描繪了觀測站周圍100 km內的定位誤差分布情況。從圖中可以看出：隨著測向精度提高，定位精度明顯提高，測向精度對定位精度產生了主要的影響。

（2）基線長度對定位精度的影響

設觀測站1的橫坐標為分別為－50 km和－70 km，觀測站2的位置分別為50 km和70 km，其他條件不變，即考慮基線長度l為50 km和70 km的情況；測向精度σθ為1°。定位精度分布如圖4所示。結合圖3和圖4可以看出：隨著基線長度的增長，定位精度明顯提高，基線長度對定位精度產生了主要的影響。

5 總結

針對不可區分的多個同類輻射源定位的問題，由于很難分辨某個測量參數是關于某個確定目標的，現有的方法也就無法獲得輻射源目標的位置信息；而位置信息場定位法可以對不可區分的多個同類輻射源定位，同時確定目標數目和多個目標的位置。在此基礎上，對基于DOA測量的位置信息場定位方法進行精度分析，仿真實驗運用橢圓概率誤差和定位誤差幾何分布來描述定位精度。結合理論指導與仿真實驗，說明了位置信息場定位法是一種有效的多目標定位方法。得出的若干結論，為該類系統的技術作戰運用提供了理論支持。

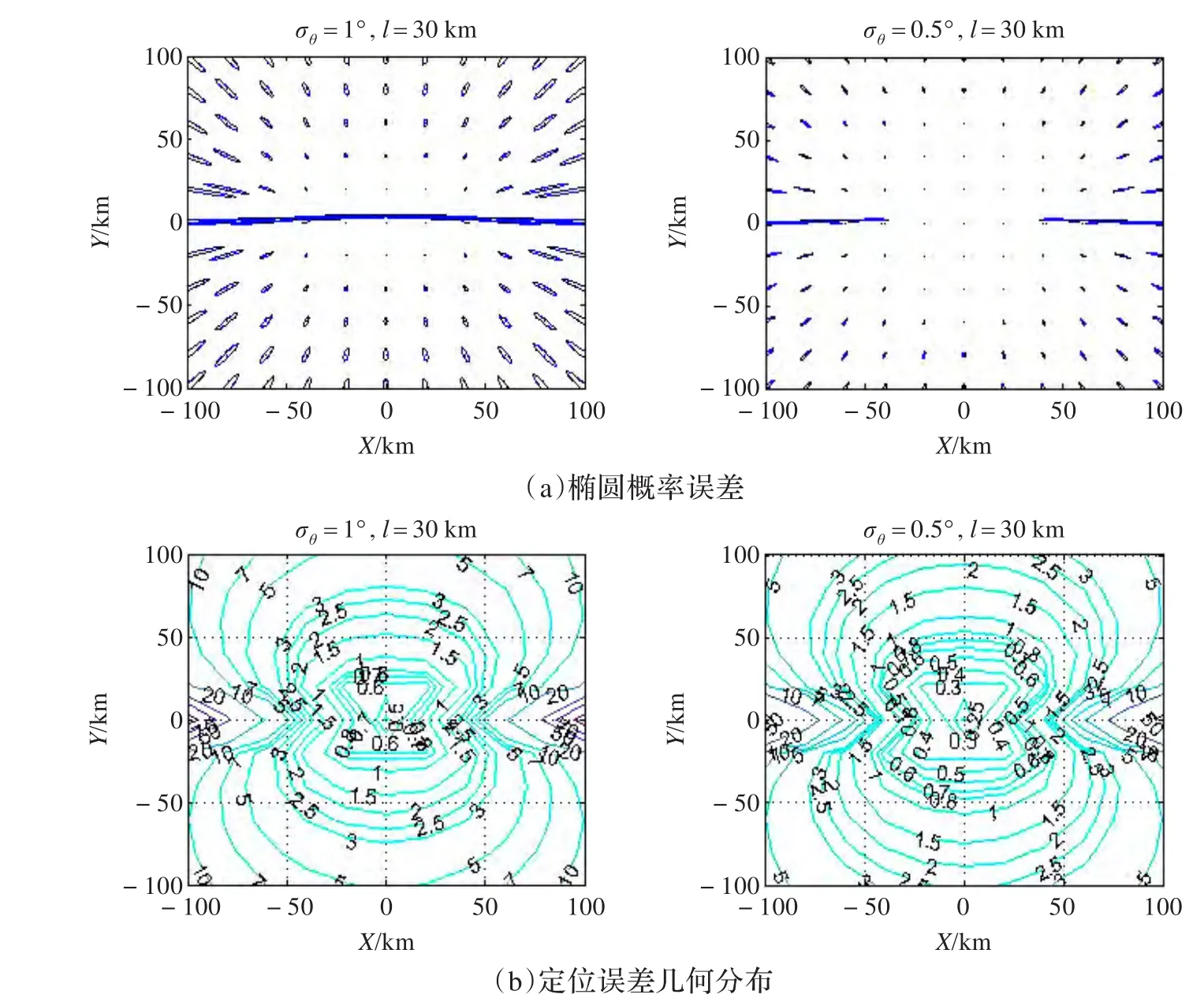
圖3 測向精度單獨對定位精度的影響

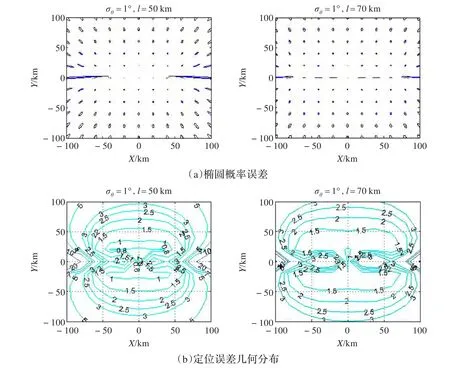
圖4 基線長度單獨對定位精度的影響

[1]Xiu J J，He Y，Wang G H，et al.Constellation of multi-sensors in bearing-only location system[J].IEE Proc-Radar Sonar Navig，2005，152（3）：215-218.

[2]Wang Xu，He Zishu.Target motion analysis in three-sensor TDOA location system[J].Information Technology Journal，2011，10（6）：1150-1160.

[3]Yeredor A，Angel E.Joint TDOA and FDOA estimation：a conditional bound and its use for optimally weighted localization[J].IEEE Trans on Signal Process，2011，59（4）：1612-1623.

[4]Li Z H，Feng D W，Sun Z K，et al.Passive location using time of arrival along with direction of arrival and its changing rate[C]//Proceedings of IEEE International Conference on Robotics，Intelligent System s and Signal Processing，Changsha，China.[S.l.]：IEEE，2003：261-265.

[5]賈興江，周一宇，郭福成.多運動站測角頻差無源定位方法研究[J].國防科技大學學報，2011，31（1）：76-80.

[6]Zhang Z H，Huang G M，Wang C P，et al.Passive location algorithm based on maximum probability density[C]//Proceedings of Conference on Information Engineering and Computer Science，2009：1-4.

[7]Amar A，Weiss A J.Localization of narrow band radio emitters based on Doppler frequency shifts[J].IEEE Trans on Signal Process，2008，56（11）：5500-5508.

[8]Weiss A J.Direct geolocation of wide band emitters based on delay and Doppler[J].IEEE Trans on Signal Process，2011，59（6）：2513-2521.

[9]羅景青.目標位置信息場分析定位法[J].電子工程學院學報，2012，31（2）：1-4.

[10]楊士英，羅景青.利用誤差橢圓消除虛假定位的算法研究[J].電子對抗技術，2004，19（5）：3-6.