基于分水嶺和形態學的圖像特征提取方法
韋 皞,張光鋒,婁國偉
(南京理工大學電子工程與光電技術學院,江蘇 南京 210094)
0 引言
由于毫米波輻被動成像能夠穿透一定厚度的非金屬介質來探測隱蔽目標,可以進行全天時全天候工作,其在公共安全檢查領域具有十分廣闊的前景[1]。為了提高成像的質量和分辨率,目前的研究方向主要集中在提高輻射計空間分辨率的硬件方法和對毫米波輻射圖像進行圖像處理的軟件方法上[2]。使用干涉成像原理的合成孔徑技術可以提高空間分辨率,但是其結構與算法復雜、成本造價較高,所以基于圖像處理技術的軟件方法較為實用和經濟。
現有的圖像特征提取算法中常用的有基于邊緣分割的微分算子,但這些算子都屬于高通線性濾波器,不適用于高頻范圍的噪聲和邊緣,故對目標邊緣模糊、毛刺噪聲較多、邊界過渡帶混疊的毫米波圖像邊緣檢測效果并不理想[3]。因此,結合分水嶺算法和形態學,文中根據目標的毫米波輻射特性提出了一種毫米波輻射圖像的特征提取算法。
1 研究基礎
毫米波輻射計進行成像工作時,會受到接收機部件因素、數據采集、周圍環境溫度和天氣等因素的影響,獲得的圖像具有較差分辨率,會出現目標邊緣模糊、毛刺噪聲較多、邊界過渡帶混疊。可以使用以下一些方法原理對圖像質量進行提高。
1.1 數學形態學
數學形態學是建立在幾何結構基礎上的一種思想,近年來也開始應用在了圖像處理和模式識別等領域。數學形態學使用結構元素來測量和提取待處理圖像中的相應形狀[4]。
形態學運算的基礎是:膨脹和腐蝕。設待處理的原 始 灰 度 圖 像 為I (x ,y) ,所 使 用 的 結 構 元 素為SE (x ,y) 。
膨脹定義為:
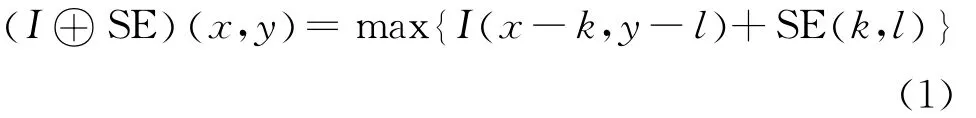
形態學膨脹運算其實是指在圖像的邊緣處理中為對象增加像素。經過膨脹處理后的圖像在灰度級上要比原始圖像更亮,所以我們可以用它來增強亮區域的邊緣,消除圖像中的暗細節。
腐蝕定義為:
形態學腐蝕運算其實是指在圖像的邊緣處理中刪除對象。經過腐蝕處理后的圖像,與膨脹運算的結果相反,在灰度級上要比原始圖像更暗。同理,我們可以用它來增強暗區域的邊緣。
形態學中的開運算與閉運算定義如下:
開運算:

閉運算:
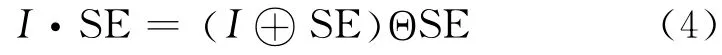
開運算能夠保持整體圖像灰度級相對不變,消除比結構元素小的亮區域,保留大的亮區域。而閉運算能夠削弱暗特征,同時不影響亮區域和背景。所以常使用開和閉運算進行圖像預處理。
高帽(Top-hat)運算是通過I x,( )y 減去其開運算,而低帽(Bottom-hat)運算是通過圖像的閉運算減去I (x ,y) 。它們分別表示為:
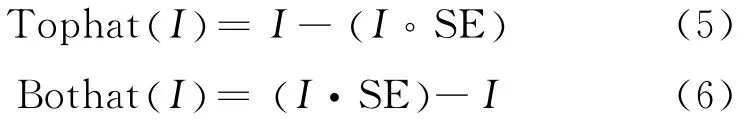
對于暗背景圖像上的亮區域,一般采用高帽運算進行處理,因為它可以去除復雜的背景并保留圖像中灰度值高的部分;而對于亮背景圖像上的暗區域,一般采用低帽運算進行處理,因為它可以增強物體之間的間隙并保留圖像中灰度值低的部分。原圖像通過加上Top-Hat 運算再減去Bottom-Hat運算,圖像可以得到增強。
1.2 邊緣檢測算子
邊緣檢測算子是基于邊緣的分割算法,它檢查每個像素的領域,在幅度和方向上對其灰度變化率進行量化。在圖像處理的研究中,邊緣檢測算子是非常活躍的課題領域。常用的邊緣檢測一階和二階微分算子有:Robert算子、Sobel算子、Prewitt算子、LOG 算子、Canny算子。
1.3 分水嶺算法
分水嶺算法的基本思想是把一副待分割圖像看作海拔不同的地形圖,圖中各像素灰度值對應地形圖中該點的海拔高度[5]。
假設一待分割灰度圖g (x ,y) 有h 個極小區域,分別用K1,K2,…,Kh表示這些區域,用F K( )i 表示極小區域值為Ki的區域。設有n次浸沒過程,第n次浸沒時的灰度值相應為n。水位從n=min+1到n=max+1變化,其中min和max分別為圖像的最小和最大灰度。用M[n]表示滿足g (x ,y) <n的所有點的集合,則可定義第n次浸沒過程與Ki相關的像素集合為Fn(Ki),它可表示為:
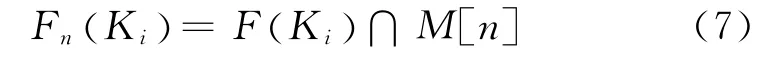
定義第n 次被水浸沒的集水區域,其并集為F[n],表示為:
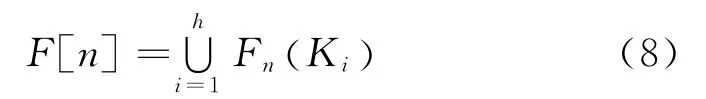
令F[min+1]=M[min+1],通過遞歸用F[n-1]計算F[n]。假設M[n]的每個連通分量p ∈P[n],存在三種情況:
1)p ∩F[n-1]的結果為空;
2)p ∩F[n-1]的結果非空,包含F[n-1]中的一個連通分量;
3)p ∩F[n-1]的結果非空,包含F[n-1]中的兩個或兩個以上連通分量。
第1)種情況沒有交集,說明此次浸沒產生了一個新的集水區域。第2)種情況說明p位于F[n-1]中的某個集水區域內。第3)種情況說明繼續浸沒時,這些集水區域中的水會融合,所以為了防止不同集水區域之間的水溢出必須在p中修建一個到多個水壩,直到達到水位的最高點。這時水壩邊界即對應著圖像的分水嶺線。
2 基于形態學和分水嶺的算法
2.1 形態濾波去噪
圖像的噪聲一般為高亮區域或者暗區域,通過結合開運算和閉運算進行形態學濾波可以有效地對圖像進行濾波降噪。根據圖像的具體結構特征來選擇開運算和閉運算的組合方式,可以使復合形態學濾波算法的效果最佳。本文先采用2×2結構元素去噪,然后再用3×3結構元素去噪,最后再用5×5結構元素進行去噪。如圖1所示,各結構元素代表圖像在各方向上的特點。

圖1 三種尺寸的結構元素Fig.1 Three structure elements
設計的復合形態學濾波結構如圖2所示。
首先用2種2×2的結構元素對原始圖像進行運算,不同的結構元素對圖像的效果不一樣,文中設計一種自適應選擇結構元素的方法。各結構元素所占的權重為:
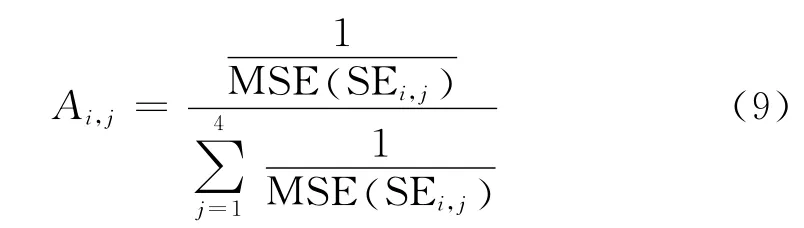
在對結構元素進行加權運算后得到M1,再用4種3×3的結構元素對M1做同樣運算得到M2,同理再用8種5×5的結構元素對M2運算得到M。式(9)中為均方誤差:
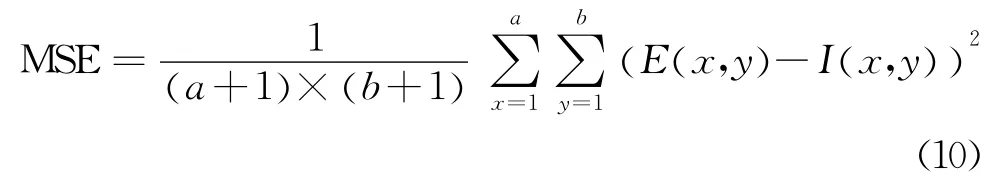
式(10)中,a、b分別為所處理圖像矩陣的行和列,E (x ,y) 為 降 噪 后 圖 像 的 灰 度 矩 陣 的 元 素,I (x ,y) 為原始圖像的灰度矩陣元素。
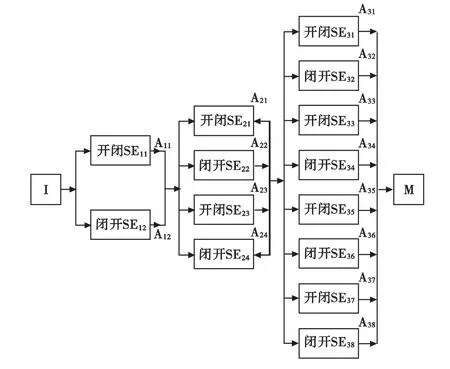
圖2 復合形態學濾波器結構Fig.2 Complex Morphological Filter Structure
2.2 基于分水嶺的圖像特征提取
1)直方圖閾值分割。由于存在大量噪聲,原始圖像中隱匿物品的邊緣部分被嚴重加寬,所以為了減少邊緣模糊,在進行形態學濾波前要先對原始圖像進行閾值處理。通過觀察原始圖像的灰度直方圖,選擇T=152對其進行閾值分割。閾值分割后的圖像即可進行形態學濾波。
2)形態學圖像增強對于經過形態學濾波后的圖像,為了更好地區分目標與背景,需要進一步對圖像進行增強。通過高帽(Top-hat)運算與低帽(Bottom-hat)運算結合的方法進行形態學增強,圖像的對比度得到提高,使得進行圖像分割后的分水嶺線更加準確。
3)形態學梯度處理。采用大小為2的圓盤結構元素,求得預處理圖像的形態梯度圖像,使得圖像中物體邊界處出現高亮度像素,而物體內部相對較低,從而為分水嶺線的定位制造了有利條件。形態學梯度運算會產生額外噪聲,通過高斯濾波器對所得圖像進行平滑處理,可以有效消除局部噪聲和毛刺。
4)分水嶺特征提取。分水嶺運算選擇待處理圖像中的極小值點作為浸沒操作的起點,所以在運算前要進行預處理,以避免過度分割。首先提取前景圖像,可以通過對增強圖像的灰度級取反再進行形態學重構得到。然后再對前景圖像進行處理得到局部極大值圖像和背景圖像。接著對梯度圖像進行極小值標定來確定浸沒操作的起點。最后對確定了起點的圖像進行分水嶺運算。
3 實驗驗證
圖3所示為原始實驗圖像,其中圖3(a)為藏匿金屬圓盤的行李箱,圖3(b)為懷抱行李箱的人,圖3(c)為原始偽彩色毫米波輻射圖像。從中可以大致看出人體和圓盤的輪廓,但邊緣比較模糊,需要進一步進行處理,從而提取出有用的特征。

圖3 原始實驗圖像Fig.3 The original experimental images
圖4所示為前期的預處理圖像,其中圖4(a)為直接轉換成的原始灰度圖像,圖4(b)為閾值分割后進行形態學濾波去噪得到的圖像,圖4(c)為形態學增強圖像。與圖4(a)對比可以明顯看出圖像質量有明顯提高,尤其是圖像的邊緣信息得到了很大的保護。圖4(d)為形態學梯度濾波后圖像,圖4(e)為前景圖像,圖4(f)為預處理圖像。
圖5為分水嶺邊緣提取所得圖像及與其他一些微分算子邊緣檢測方法的對比,其中圖5(a)為canny算子,圖5(b)為log算子,圖5(c)為prewitt算子,圖5(d)為sobel算子,圖5(e)為分水嶺邊緣提取圖像。圖5(f)為分水嶺彩色分割圖像,可以清晰看到所需檢測金屬圓盤和人體輪廓特征。可以看出分水嶺算法的處理效果優于其他幾種微分算子。由于成像過程中受到各種噪聲的干擾,原始的毫米波輻射圖像質量較差。采用形態學降噪和增強后,有效去除了圖像中的噪聲并在很大程度上保護了圖像的原始信息。通過分水嶺算法進行分割得到的圖像可清楚看到人體和金屬圓盤的輪廓。前期的預處理工作有效避免了圖像的過分割,提高了結果的準確性。
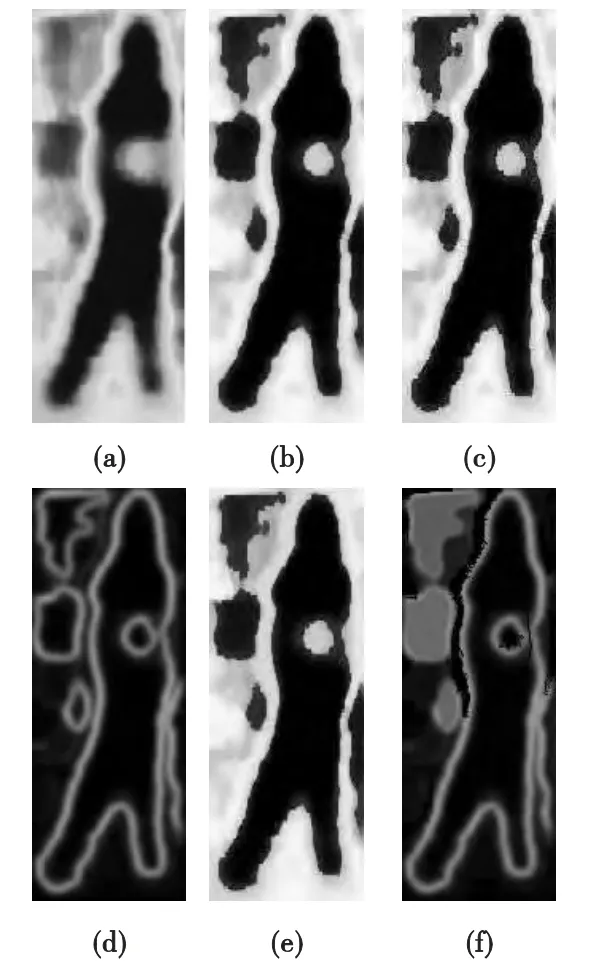
圖4 實驗預處理圖像Fig.4 Pre-processed Experimental Images
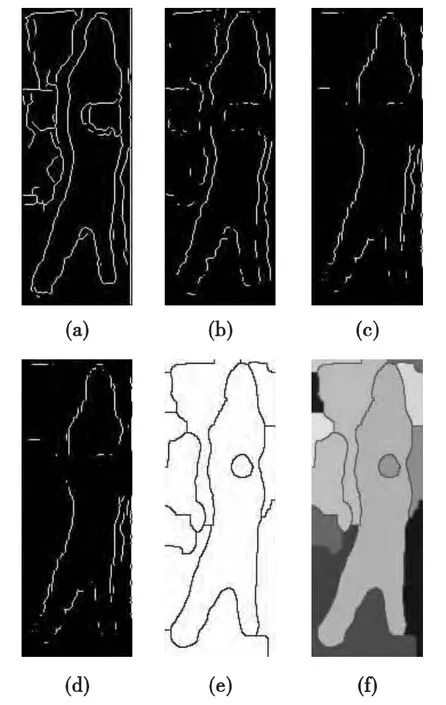
圖5 分水嶺邊緣提取和微分算子對比Fig.5 Different results based on watershed and differential operators
4 結論
本文提出了基于分水嶺和形態學的毫米波輻射圖像特征提取方法。該方法通過自適應的形態學復合濾波方法對毫米波輻射圖像進行降噪處理,并對濾波后的圖像使用分水嶺算法進行圖像分割,是對毫米波輻射圖像進行特征提取分析的初步嘗試。試驗表明,該方法可以有效提高圖像的質量,清晰反映出金屬目標的輪廓,在安檢領域必將具有很好的應用前景。但該方法對于一些亮溫差值較小區域的分割效果較差,后續研究可考慮結合局部分割的方法[5]對隱匿物品的特征做深入的分析與研究。
[1]Gomez-Maqueda I,Almorox-Gonzalez P,Callejero-Andres C,et al.A millimeter-wave imager using an illumi-nating source[Application Notes][J].IEEE Microwave Magazine,2013,14(4):132-138.
[2]王本慶,李興國.被動毫米波圖像恢復的偏微分方程方法[J].探測與控制學報,2009,31(5):25-28.
[3]趙凌,張祖蔭,郭偉.基于數學形態學的毫米波圖像邊緣檢測方法[J].國土資源遙感,2006(4):19-22.
[4]Levner I,Hong Zhang.Classification-driven watershed segmentation[J].IEEE Transactions on Image Processing,2007,16(5):1437-1445.
[5]Cousty J,Bertrand G,Najman L,et al.Watershed cuts:Minimum spanning forests and the drop of water principle[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(8):1362-1374.

