傳感器安裝對電磁轉矩測量的影響

高 楷，郭軍獻，李福松

（1.機電動態控制重點實驗室，陜西 西安 710065；2.西安機電信息技術研究所，陜西 西安 710065）

0 引言

采用精確制導組件（Precision Guidance Kit，PGK）進行彈道修正的二維彈道修正引信具有“一維動作，二維修正”的功能，可以使常規彈藥獲得精確打擊能力并降低作戰成本，在未來具有很高的使用價值。PGK 控制組件中電機不僅作為發電裝置，還作為控制裝置使用，其電磁轉矩與系統的負載和轉速有關，電磁轉矩隨負載／轉速變化特性影響著控制組件的修正能力和控制精度。因此了解控制組件中電機電磁轉矩隨負載／轉速變化特性是實現修正功能及控制精度的先決條件。通過傳感器對電機進行電磁轉矩測量可得到電磁轉矩隨負載／轉速的動態特性。對控制電機電磁轉矩的測量精度應有合適的要求，才能提供可靠的數據給控制端，從而對彈道進行精確的修正。

在對電機電磁轉矩進行測量時，需考慮傳感器安裝角度偏差產生的彎矩對測量精度的影響。目前所查閱到的文獻中，對傳感器安裝時角度偏差引起的誤差的研究都只是理論上大致分析了角度偏差對測量精度的影響［1-2］，尚未見分析測量精度與安裝偏差角度關系的文章。所以本文提出了電磁轉矩測量精度對傳感器安裝偏差角度要求的計算公式。

1 電磁轉矩測量和傳感器安裝

在對電磁轉矩進行測量時，除了傳感器安裝角度偏差對測量精度產生誤差影響外，傳感器機械性能引起的誤差［3］和傳感器應變片貼裝位置偏差引起的誤差［4］也會對測量精度產生影響，通過選取高規格的傳感器可以減弱測量帶來的誤差影響。

要得到精確的電磁轉矩測量數據，在安裝傳感器時應保證傳感器的軸心線與被測系統在同一軸線上。在安裝中，如果傳感器的安裝產生一定的角度偏差，傳感器的自身重力會使測試軸上產生彎矩，彎矩在傳動軸上產生附加扭矩，使得傳感器測量到的轉矩值增大，影響電磁轉矩的測量精度［5］。為了說明角度偏差引起的誤差，以傳感器傳動軸為對象進行應力分析。根據力學理論在傳感器傳動軸上取一個正六邊形的單元體［6］，如圖1所示。其中z 軸為旋轉軸，σx為彎矩產生的正應力，τx、τy為電磁轉矩產生的剪應力，且τx=τy。

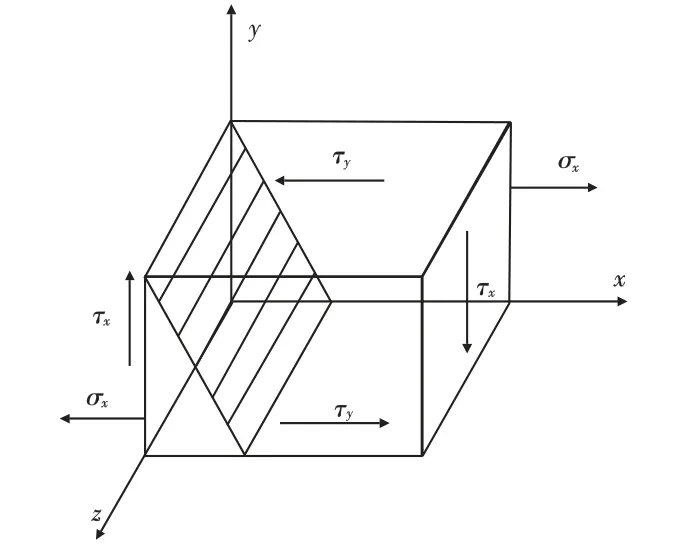
圖1 正六邊形同時受扭矩與彎矩的應力分析Fig.1 Stress analysis of hexagon by torque and bending moment

在單元體內任意取一斜截面，如圖2所示，α 為斜截面外法線與x 軸的夾角。

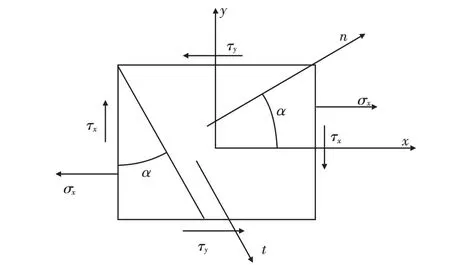
圖2 單元體斜截面分解應力分析Fig.2 Section stress analysis of unit cell inclined decomposition

由力學理論［7］可知當傳動軸上存在彎矩時，在單元體斜截面上產生的切線應力為轉矩與彎矩共同作用的結果：

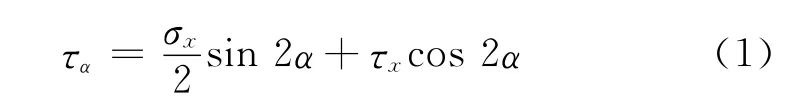
傳動軸上，在軸線與軸圓柱面上成135°和45°角的方向上存在最大的且相等的壓應力和拉應力［8］。當傳感器安裝不存在角度偏差（理想情況）時，軸上只存在電磁轉矩作用，此時單元體上的剪應力僅由電磁轉矩產生，通過應變式傳感器的應變片對所受應力的信號傳遞，可得到電磁轉矩；當傳感器存在角度偏差時，軸上除了電磁轉矩作用外，傳感器自身的重力對軸產生彎矩影響，此時單元體上的剪應力由電磁轉矩與彎矩共同產生。

2 傳感器安裝角度計算公式

通過對軸上單元體所受的電磁轉矩與彎矩所產生的應力進行分析，分別得出當軸只受電磁轉矩和電磁轉矩與彎矩同時作用下的應力情況，通過公式的推導，最終得出傳感器安裝角度偏差時偏差角度與測量精度的關系式。

當傳動軸只受電磁轉矩的情況時，轉矩產生的剪應力：

由式（1）可以得到當α=45°時轉矩與彎矩共同作用下的剪應力為：

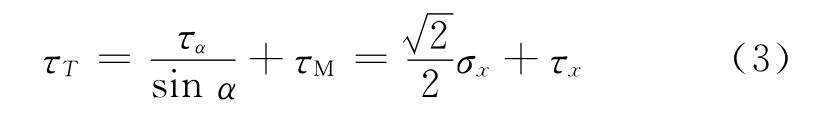
式中：τx=M／wp，wp為軸截面極距，M 為傳動軸所受電磁轉矩（N·m），σx= Mny／μWz，Mn=mgLsinθ為傳動軸所受彎矩（N·m），m 為傳感器質量，L 為傳動軸長度，y 為單元體到中性軸的垂直距離（m），μ 為被測軸的泊松比，Wz為抗彎截面系數。

當彎矩與轉矩共同作用時，測量到的轉矩為：

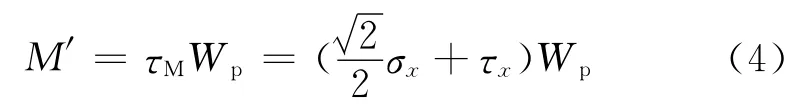
由此可得傳感器安裝角度偏差引起的轉矩誤差為：

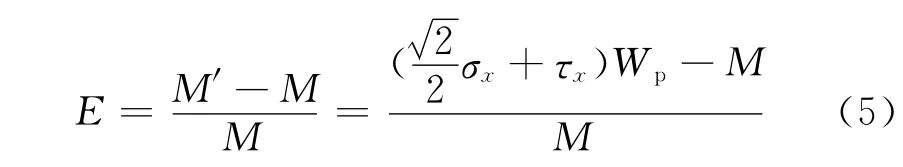
測量系統對電磁轉矩的測量誤差要求為E ≤q%（6），將參數τx，σx，Wp，M 代入式（6）可得：

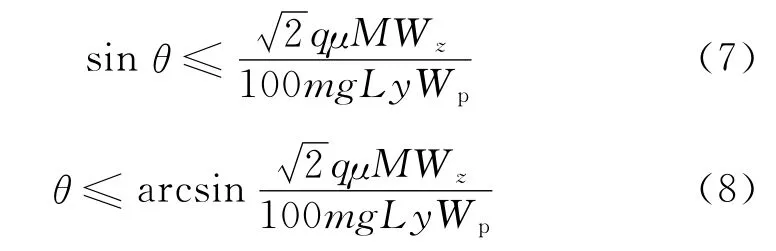
由式（7）可知，當傳感器安裝偏差角度為（8）時，可以滿足安裝角度偏差下的測量精度要求。

3 傳感器安裝角度偏差理論計算與仿真驗證

為了驗證上述理論分析的正確性，對所研究的電磁轉矩測試系統進行了理論計算，同時利用ANSYS軟件進行了數值仿真。

假設被測系統的參數如下：傳感器質量M=0.5kg，泊松比為0.3，傳動軸軸長為20 mm，單元體與中性軸的垂直距離為15mm，電機產生的電磁轉矩的變化范圍為（5 ～30N·mm）。根據公式（7）可知，較大的電磁轉矩所引起的偏差角度也相對較大，因此，角度偏差應小于最小電磁轉矩所對應的的安裝偏差角度。

通過分析對10種測量精度進行了計算與仿真的驗證，其中100%為無誤差情況。利用ANSYS仿真軟件對傳感器傳動軸進行了建模，對傳動軸進行了10種情況下的轉軸所受應力仿真，得到了10種情況下傳動軸的應力狀態，將數據代入式（6）中得到不同測量精度下偏差角度的仿真結果，圖3-6為其中的4種情況。

圖3 測量精度為100%Fig.3 Measurement accuracy of 100%

圖4 測量精度為99%Fig.4 Measurement accuracy of 99%

圖5 測量精度為98.5%Fig.5 Measurement accuracy of 98.5%

圖6 測量精度為98%Fig.6 Measurement accuracy of 98%

當無角度偏差時，傳動軸上所受應力為τ初；當存在角度偏差時，傳動軸上所受應力為τ偏。將100%測量精度情況下的應力與其他測量精度情況下的應力代入式（5）進行計算，得到不同測量精度下偏差角度的理論計算結果，其中精度為ξ=1-E。表1為10種情況下測量精度的仿真結果與理論計算結果。

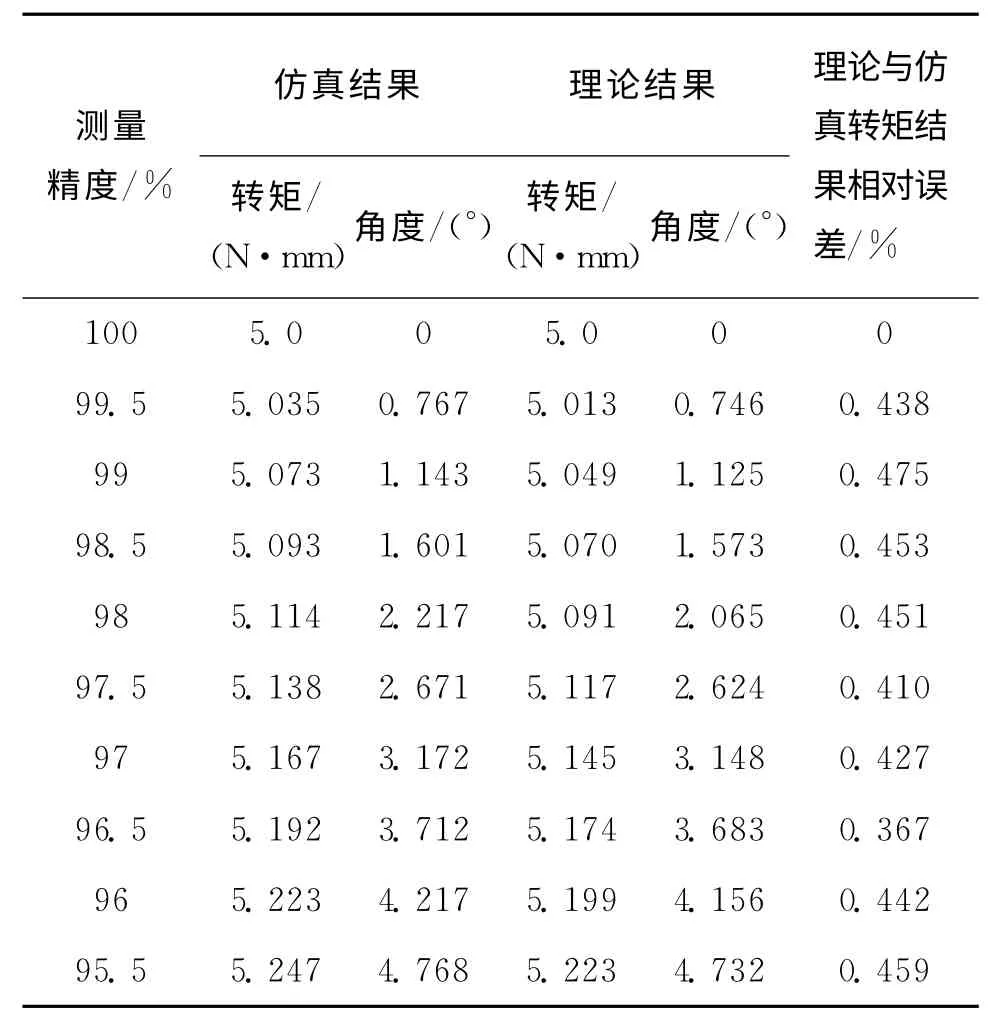
表1 10種情況下測量精度的仿真結果與理論計算結果Tab.1 10Cases measurement precision of simulation results with the theoretical calculation results

由表1可得安裝偏差角度與測量精度的關系，如圖7所示。偏差角度越大，產生的誤差越大，偏差角度與測量精度在一定精度范圍內近似為線性關系，由表可知理論計算結果與仿真結果基本一致。

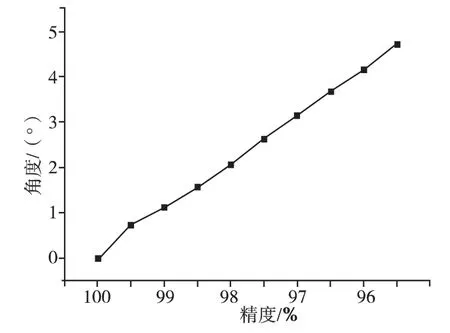
圖7 安裝偏差角度與測量精度的關系Fig.7 Relationship between installation deviation angle and measurement accuracy

4 結論

本文提出了電磁轉矩測量精度對傳感器安裝偏差角度要求的計算公式。該公式中與角度有關的因素有電機電磁轉矩，測量精度和傳動軸自身的幾何特性，其中角度與電機產生的電磁轉矩與測量精度成正比，與傳動軸自身的幾何特性成反比。通過ANSYS軟件對10種情況進行的仿真與理論結果比較，表明理論計算結果與仿真結果基本一致，測量精度與安裝偏差角度在一定精度范圍內近似為線性關系。利用該公式可得出不同精度要求下的安裝偏差角度要求，得到安裝偏差角度與測量精度的關系，為電磁轉矩測量中傳感器安裝偏差控制提供參考。接下來將利用測量系統進行試驗測量，為理論分析提供進一步的數據驗證。

［1］馬龍龍.應變式傳動軸功率測試系統設計與研究［D］.太原：中北大學，2011.

［2］張曉強.應變式高準確度動態扭矩測量儀的研制［D］.哈爾濱：哈爾濱理工大學，2003.

［3］禹精達，朱暉.傳動軸扭矩誤差測量分析［J］.機械研究與應用，2011（04）：4-5.

［4］高曉丁，胥光申，王錦.電阻應變片貼裝方位偏差對測量結果的影響［J］.西安石油學院學報，2001（16）：41-43.

［5］趙思宏，范惠林.電機轉矩轉速測量方法的分析［J］.光學精密工程，2002（10）：290-294.

［6］孫望超，李冬華.工程力學［M］.北京：科學技術出版社，1994.

［7］張新占.材料力學［M］.西安：西北工業大學出版社，2006.

［8］張有頤.轉矩測量技術［M］.北京：計量出版社，1996.