理解教學價值 追求設計優化

【摘 要】教學立意源于對教學的價值判斷，它取決于教師對教材的理解、對學生的理解和對教學的理解。教學價值是對“教什么”的定位選擇，是對“為什么這樣教”的概括詮釋，是對“怎么教”的有力保障。為此，教學價值是教學設計的靈魂，理解和把握準數學的教學價值，就顯得尤為重要。本文從“從問題到方程”這個課例，對教學價值的挖掘與選擇進行研究與思考。

【關鍵詞】教學價值 價值判斷 教學預設 價值追思

一、課例背景分析及價值判斷

蘇科版《數學》教材七年級上冊“第四章一元一次方程” “4.1從問題到方程”這節內容，為研究方程相關問題提供了一個的新視角，也是義務教育課程標準理念下教材編寫的一個新突破。教材提供了下列三個教學素材。

素材一：怎樣描述圖中天平平衡所表示的數量之間的相等關系？

素材二：籃球聯賽規則規定，勝一場得2分，負一場得1分，該籃球隊賽了12場，共得20分。怎樣描述其中數量之間的相等關系？

素材三：我國古代問題：以繩測井，若將繩三折測之，繩多4尺；若將繩四折測之，繩多1尺。繩長、井深各幾何？

面對上述三個問題，首先需要思考的是提供的三個素材為什么要用方程來解決？用小學算術的方法不可以嗎？弄清這個問題，學生才能認識“從問題到方程”中的“到”的價值，才能體現“從問題到方程”這節教學內容的本質訴求。那么，教材中提供的三個素材能夠回答為什么要用方程來解決問題嗎？如果不能回答，應該對教材作怎樣的改造？這些問題要引起我們的關注和思考。

教材是采用“從天平到方程”導入新課的，這樣的導入比較直觀，學生容易接受。但是，對一個問題為什么不用學生已熟悉的算術方法去解，而要用方程方法去解揭示得不夠。因此，在教學中必須增加環節，讓學生明白用方程解決問題的來龍去脈。

本著這樣的想法，我對教材提供的素材作如下改造：

可以選用“雞兔同籠”問題作為研究問題的導入情境。第一，它是學生目前最為熟悉的情境之一。在小學里學生都接觸，甚至還作為專題研究過；二是用它的“算術解法”（實是假設法）過渡到“方程解法”（也是假設法），既能顯示從問題“到”方程的思維過程，更能凸顯方程的本質，讓學生清楚地知道，用方程去解決問題，第一步為什么要先設出未知數（設未知數主要是因為方程是“假設法”下的產物，“設”字實為“假設”之意）；三是此問題中的數量關系簡明、簡單，在學生現有的心智水平下，易用字母表示出來，從而容易將問題方程化，實現從問題“到”方程。

另一方面，改造教材中的問題模型。教材中提供的問題是零散的，得到的方程全是各不相同的，要想“通過從問題到方程，讓學生初步感受方程是刻畫現實世界相等關系的有效模型”，恐難奏效。為此，可以用“雞兔同籠”中的方程為模型，以組織學生“秋游”為主題（上這節課時正值學校準備組織秋游活動），在“主題式”探究活動中，讓學生初步感受方程是刻畫現實世界相等關系的有效模型，更有實效性和教育性。

根據上述背景分析，本節內容的教學預設可按下列方式進行。

二、基于價值判斷的教學預設

問題1 “雞兔同籠，上有三十五個頭，下有九十四只足，問雞、兔各多少？”這是經典的古代名題，請同學們回憶一下，在小學里你是怎么解決這個問題的？

解答期盼： （1）“砍足法”。假設把兔子的足砍去一半， 則有３５×2=70（只）足，那么被砍去的足有94-70=24（只），故有24÷2=12（只）兔子。（2）“兔立法”。假設讓兔子全“站立”起來，那么雞、兔共有35×2=70（只）足，而實際多了94-70=24（只）足，故有24÷2=12（只）兔子。（3）“公平法”。兔有4只足，雞有2只足，這樣對雞是否有些不公平？不過兔子沒有翅膀，而雞有2只翅膀，這樣一想，也能算是公平了。則又可假設把雞的兩只翅膀也算足的話，那么就有35×4=140（只）足，這就說明雞有46÷2=23（只），故原來有２３（只）雞。

問題2 上述解決問題的方法主要運用的是小學數學知識，這幾種方法有什么共同點？

解答期盼： 有些事情雖然沒有發生，但我們可以在想象中假設它發生了，于是出現了合乎解決問題的情境，從而獲得問題的答案。故上述解法，其實質就是“假設法”。

問題3 我們能否沿著假設法的思路，通過“用字母表示數”的方法來解決該問題呢？

解答期盼： （1）假設雞有x只，則兔有（35-x）只。 根據雞、兔共有94只足，就有2x+4（35-x）=94。余下的問題就變成學生熟知的問題了。（2）上面解答的思路是將小學階段學習的“假設法”遷移到初中數學中，用方程來解決問題。

問題4 秋天是個收獲的季節，學校準備組織部分同學去秋游。小明是秋游活動的負責人，你們能幫他解決下列問題嗎？

請看題：學校組織七年級94名三好學生到玄武湖劃船秋游，共用船35條，若每條大船可以坐4人，每條小船可以坐2人，如果小船有x條，那么可得方程 。

解答期盼： （1）將解決“雞兔同籠”問題的經驗延伸到“秋游劃船”問題上來，再次經歷根據未知數的意義列出方程的過程，體會用方程解決問題的思想方法。（2）反觀列出的方程，產生“同一方程可表示不同問題背景”的意識，對“數學模型”有一種朦朧的感覺。

問題5 俗話說，兵馬未動，糧草先行。現決定秋游活動自帶水果，你能幫小明當好這個后勤部長嗎？請看題：用94元錢買蘋果和橘子共35斤，已知蘋果4元每斤，橘子2元每斤。如果買了x斤橘子，那么可得方程 。

解答期盼： （1）對從問題到方程能有一個比較常態的轉化。（2）初步形成“同一方程可表示不同的問題背景”的觀念，對“方程是刻畫現實世界數量相等關系的一種有效的數學模型”有一個初步的認識。

問題6 當秋游回來，小華向小明請教了四個問題，你們能幫小華解決嗎？請看題：

（1）已知師傅每小時做4個零件，徒弟每小時做2個零件。現師、徒兩人在35小時內完成94個零件的加工任務。那么徒弟做了多少小時（用方程表示）？

解答期盼： （1）對“從問題到方程”能有一個比較規范化的轉化。即首先要確定未知數，并能用字母表示出來，然后根據已知數、未知數的意義列出方程。（2）進一步讓學生體驗“方程是刻畫現實世界數量相等關系的一種有效的數學模型”的思想。即不同的問題背景，可用同一方程（數學模型）將之表示出來，再次加深對２x＋４（３５－x）＝９４理解，再次體驗模型思想。

（2）在一次電腦知識競賽中共有20道題。對于每道題，答對了得5分，答錯了或不答的扣3分，鄧民同學得了84分，則他答對多少道題（用方程表示）？

解答期盼： ①可以根據“答對的得分－答錯或不答的扣分=84”，列出方程。設答對y道題，那么答錯（２０－y）道題，則可得方程５y－３（２０－y）＝８４。②對模型化思想有進一步認識，讓學生認識到不同的問題背景，可用不同的方程（數學模型）來表示。

（3）籃球聯賽規則規定，勝一場得2分，負一場得1分，該籃球隊賽了12場，共得20分。怎樣描述其中數量之間的相等關系？

（4）我國古代問題：以繩測井，若將繩三折測之，繩多4尺；若將繩四折測之，繩多1尺。繩長、井深各幾何？

解答期盼： 通過對上面（3）（4）二題的探究，期盼學生有下列之效：①根據本節課前面的思維活動積累下來的用方程解決問題的經驗，對將實際問題轉化成方程的數學建模技能有一個鞏固提升的過程。②通過探究得到的9個方程，分析其“式結構”特征，為歸納一元一次方程的概念奠定基礎。

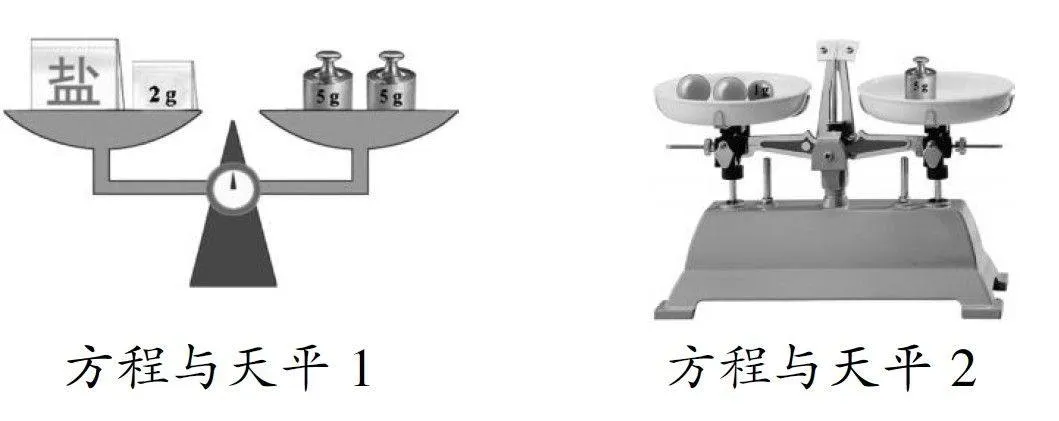
問題7 現實生活中充滿了大量的相等關系，方程的思想無處不在，現在就讓我們再去感受一下方程的思想。

如圖所示（方程與天平1），可以得到的方程為： x+2=10

如圖所示天平（方程與天平2），可以得到什么樣的方程？

解答期盼： 體會方程是解決實際問題中相等數量關系的有效模型，從天平的原理中，體會數學的應用價值，讓學生快樂地學習數學。

三、課例設計中“到”的歷程

本預設主要從下面三方面體現“到”的歷程，凸顯教學內容中的“到”的價值。

1．問題“到”方程。

通過探究“砍足法”“兔立法”“公平法”等解法，引導學生經歷從小學算術（算法）到中學數學（方程）的探索歷程，放大“到”的過程。這一過程也就是讓學生清晰體會從“算術法”到“方程法”的過程，是一個“形異實同”的過程，是一個將新知識納入到舊知識結構中去的過程。關鍵是本預設從舊知識出發，引導學生積極思維，有效參與，在合理繼承“算術法”的內核（實為假設法）的前提下，又不失新意（提示了方程法的實質也為假設法），實現了從小學算術法向初中方程法的巧妙過渡，有力地激發了學生對數學的美好情感。

2．從方程“到”模型。

主題式探究是圍繞某一中心問題展開“形散神不散”的探究活動。本預設，通過對“雞兔同籠”問題的探究形成的基礎，在以“秋游”為主題的系列問題探究中，凸顯模型思想，挖掘“到”的價值。一是“同一個方程模型可表述不同的問題背景”，讓學生感受方程的本質美；二是形成“不同的方程可以表述不同背景”的經驗。

3.從模型“到”天平。

在研究了一些問題之后，將學生的視角從“方程”引入到“天平”，來感悟“方程與天平”的聯系，那么學生對天平的認識，必然是不僅僅停留在小學那種簡單的在“形”中“看”，而是在“數”中“思”，即由形象思維上升“到”理性思維，有力地落實了《數學課程標準》提出“螺旋上升”的要求。

四、對教學中“到”的價值的追思

1．從數學知識“到”學科智慧。

數學學科是一個讓人聰明起來的學科，是一個讓人增長智慧的學科。要體現上述思想，就教材教教材不行，就知識教知識也不行。必須要跳出教材教知識，跳出知識得經驗，跳出經驗長智慧。作為方程教學的首節內容教學要點，不是怎樣教會學生將問題用“意會法”、“表格法”、“圖象法”轉化成方程的技能，而應讓學生如何想“到”用方程的思想去解決問題，即不僅是知識層面和方法層面的教育，而應上升到智慧層面、素質層面的教育。好的數學教學活動，應突出數學的特點，揭示數學知識產生的自然性與合理性，要基于感性發展理性，讓數學教學閃耀理性、智慧的光芒。

2．從課時目標“到”課程目標。

教學目標是教學活動的出發點與落腳點，這句話切中了把握教學目標的重要性。正因為如此，教師們才熱衷于課時目標的分解與實現。在此理念下，“將數學分解成支離破碎的知識，過分關注知識的細枝末節，在非本質的形式上打轉轉、做文章，講究立竿見影，還冠以學有用的數學、學實惠的數學”，這樣在某種程度上講是有可能利于學生掌握一些知識與技能，但也會讓學生有只見樹木不見森林，看不到隱藏在數學知識后面的數學本質、數學思想方法，導致課程目標難以實現。因此，在教學中不僅要注意將課程目標分解成課時目標，而且還要善于將課時目標反作用于課程目標，完成數學學科的教學任務。

3．從數學教學“到”數學育人。

數學學習在人的發展過程中有著不可替代的重要性和必要性。數學教育之根本意義在于培養求真理、講道理、懂科學、有智慧、究根底、會思考的人。為此，數學教師要有“大數學學科思想”的胸懷與膽識，將數學教學上升到數學育人的層面上來開發教學資源。要把數學教學作為人類活動的數學來對待，用研究科學的方法來研究數學；要把數學教學作為理性思維的數學來對待，用理性思維思考數學；要把數學教學作為文化素養來對待，用數學素養來滋潤學生的心靈。

【參考文獻】

［１］卜以樓．凸顯遷移能力的教學設計個案［J］．中國數學教育（初中），2009（11）

［２］卜以樓．要在“靜”界中發展學生的思維能力［J］． 教學月刊·中學理科版，2012（4）

［３］教育部.義務教育數學課程標準（2011年版）［S］．北京：北京師范大學出版社，2012

［４］義務教育教科書·數學（七年級上冊）［Ｔ］．南京：江蘇科技出版社，2012