鎳銅合金NCu30-4-2-1電渣熔鑄件的熱變形行為

劉德林，陶春虎，關文秀，姜 濤，張 兵

(北京航空材料研究院 航空材料檢測與評價北京市重點實驗室，北京 100095)

蒙乃爾合金是以Ni為基的Ni-Cu合金，最早由美國國際鎳公司開發，其典型成分為 70%Ni和30%Cu(質量分數)，這是鎳基耐蝕合金中應用最廣泛的合金[1?2]。鎳銅合金NCu30-4-2-1是Ni-Cu-Si-Fe-Mn系彌散硬化型高耐磨性Ni基合金，通常稱為含硅蒙乃爾合金，該合金屬于沉淀硬化型，即通過合適的熱處理能夠使Si以金屬間化合物Ni3Si相形式從基體中析出，在晶界和晶粒內呈彌散分布，大大提高合金的強度和硬度。與其他蒙乃爾合金相比，NCu30-4-2-1由于硅含量較高(質量分數為4%)，具有高硬度、高強度、優良的耐磨性和抗粘合性的特點，因而適合用于制造航空燃油裝置及其他要求工作穩定的精密摩擦件[3?4]。該合金不能進行熱處理強化，主要是通過固溶強化和熱加工工藝來提高合金的力學性能。研究表明[5]，該合金擠壓態的塑性較鑄態有較大提高。采用普通鑄造工藝制備的鎳銅合金NCu30-4-2-1鑄棒心部不可避免存在縮孔等鑄造缺陷，而且由于正向擠壓成形時坯料心部的變形量小于表面的變形量，從而擠壓成形后擠壓棒心部仍存在原始鑄造缺陷，導致心部材料的塑性較差，滿足不了使用要求。而采用電渣熔鑄工藝制備的NCu30-4-2-1鑄件具有純凈度高、組織致密、成分均勻等優點，可改善擠壓制品的力學性能。ZHOU等[6]對鎳銅合金 NCu30-4-2-1摩擦磨損特性的研究表明：鑄態合金的摩擦磨損性能較差；YANG等[7]對硅在該合金中的行為進行了研究。然而，目前尚未見關于NCu30-4-2-1電渣熔鑄件熱變形行為的研究報道。為此，本文作者對鎳銅合金NCu30-4-2-1電渣熔鑄件進行等溫壓縮實驗，研究該合金的熱變形流變應力行為及顯微組織演化規律，為制定與優化該合金的熱擠壓工藝提供理論依據。

1 實驗

1.1 實驗材料

本實驗所用的鎳銅合金NCu30-4-2-1是由北京航空材料研究院制備的電渣重熔鑄棒，其化學成分(質量分數)如下：Cu 29.0%～31.0%，Si 3.8%～4.5%，Fe 1.5%～2.5%，Mn 0.8%～1.5%，C不大于0.2%，Al不大于0.30%，Mg不大于0.10%，S不大于0.02%。沿鑄棒軸向切取d 10 mm×15 mm的圓柱試樣。

1.2 實驗方法

將加工好的試樣在Gleeble?3800熱模擬機上進行等溫壓縮實驗，壓縮變形溫度為900～1 100 ℃，應變速率為0.01～10 s?1，壓縮率為60%。壓縮變形前保溫5 min，壓縮時試樣兩端粘貼潤滑劑片，變形后立即對試樣進行水淬，以保留其高溫變形組織，水淬延遲時間約為1 s。采用Gleeble?3800熱模擬機的計算機系統自動采集應力、應變、位移、溫度及時間等數據。將熱壓縮后的試樣在中間垂直上下表面切開，采用OLYMPUS PME3型光學顯微鏡觀察合金壓縮變形后的金相組織。

2 結果與討論

2.1 真應力—真應變曲線

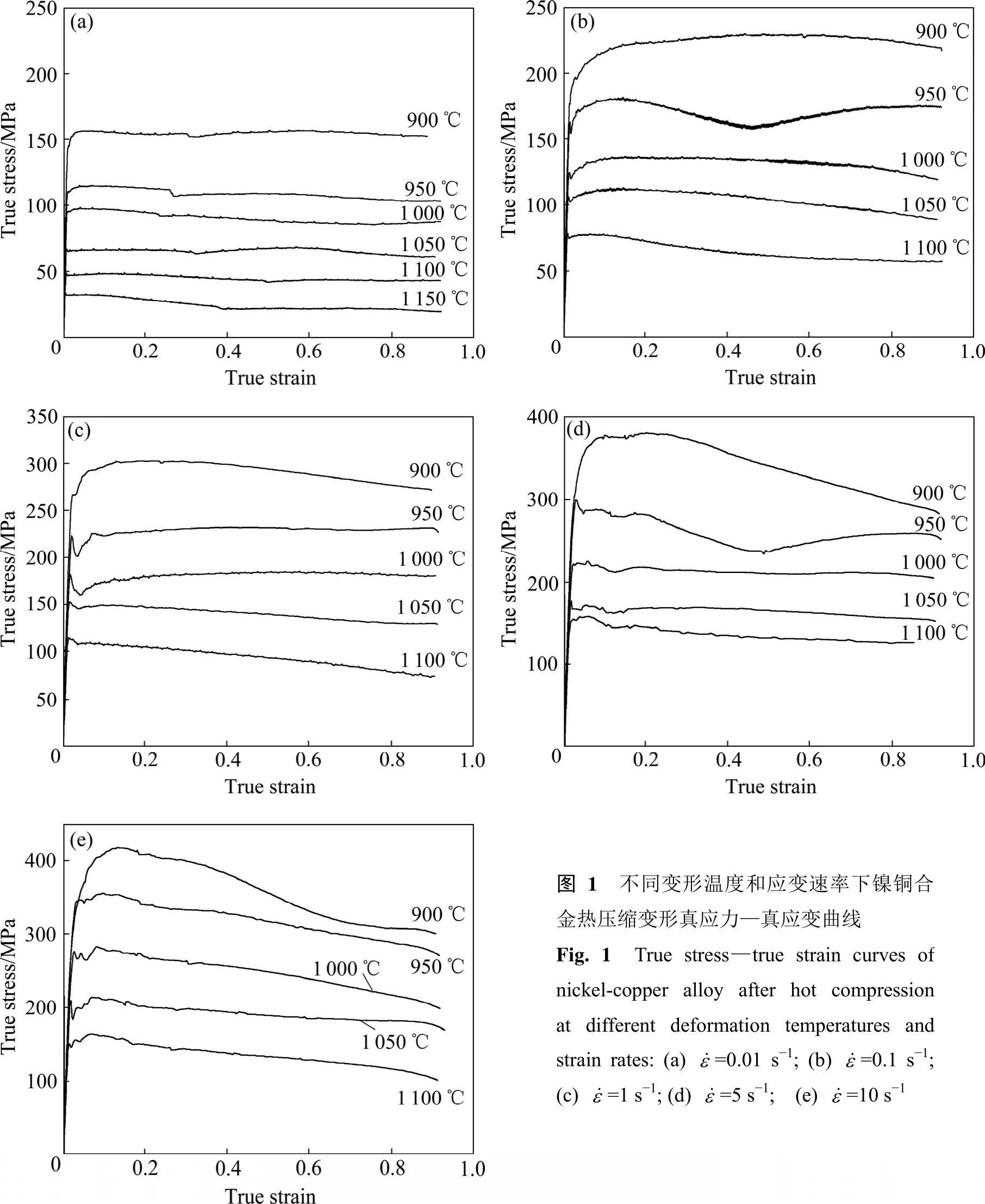
圖1所示為鎳銅合金NCu30-4-2-1在高溫等溫壓縮變形的真應力—真應變曲線。由圖1可見，在變形溫度900～1 100 ℃和應變速率為0.01～10 s?1的條件下，流變應力隨應變量的增加而迅速升高，達到峰值后鑄件下降至穩態值，進入穩態變形階段。該現象是由于合金在塑性變形過程中，加工硬化和動態軟化同時進行。在變形初期，外加應力使位錯密度增加，位錯間的交互作用增大了位錯運動的阻力，交滑移引起的軟化不足以克服位錯密度增加帶來的硬化，因此，在峰值應力之前加工硬化處于主導地位，應力水平迅速上升；隨著應變量的增加，晶內儲存能逐漸增加，動態軟化與加工硬化達到動態平衡，流變應力基本不變[8]。

從圖1還可以看出，在同一應變速率下，流變應力隨溫度的升高明顯下降，這是由于隨著溫度的升高，熱激活作用增加，原子動能增加，位錯運動的阻力下降，空位和間隙原子等點缺陷也更加活躍，因而產生動態回復及動態再結晶引起的軟化程度也隨溫度的升高而增大，導致合金的流變應力降低。在同一溫度下，該合金的流變應力隨應變速率的增加而增大，說明該合金是正應變速率敏感材料。

2.2 流變應力方程

在熱變形過程中，材料在任何應變或穩態下的高溫流變應力σ強烈地取決于變形溫度 T和應變速率，通常可采用SELLARS和MCTEGART[9]提出的雙曲正弦形式加以描述：

式中：)(σF為應力的函數，在不同的條件下分別可以表示為以下3種形式：

ασ＜0.8時，

ασ＞1.2時，

所有應力下，

對所有應力狀態，式(1)可表示為

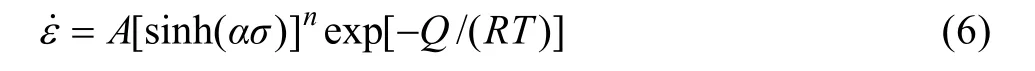
式中：α、n、A、β為常數，α為應力水平參數(mm2·N?1)，n 為應力指數，A 為結構因子(s?1)，Q 為熱激活能，是材料在熱變形過程中重要的力學性能參數，反映材料熱變形的難易程度；T為絕對溫度；R為摩爾氣體常數；為應變速率。求出α、n、A、Q，即可描述材料的高溫流變特性。大量的研究結果表明[10?12]，式(6)能較好地描述壓縮、擠壓、扭轉等常規的熱加工變形。

另外，SELLARS和TEGART提出并用實驗驗證了熱變形條件通常可用溫度補償的應變速率因子Zener-Hollomon參數Z來描述[9,13]：

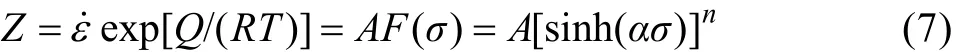
研究表明，在低應力水平下，流變應力σ和Z可用指數關系描述，而在高應力水平下可以冪指數關系描述，在整個應力水平下可用雙曲函數關系描述。實際上，式(7)在形式上與式(6)是一致的。

對式(2)和(3)兩邊取對數：

ασ＜0.8時，

ασ＞1.2時，

由式(6)可得：

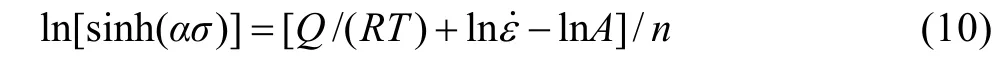
考慮到峰值應力均出現在應變較小的時刻，溫升修正前后峰值變化并不明顯，為方便計算，取相應、T條件下的真實峰值應力，分別以σln和ln 為坐標作圖，結果如圖2所示。由式(8)可知，直線ln—σln斜率，設為n1；由式(9)可知，直線ln —σ的斜率，設為β。采用最小二乘法線性回歸，n1取圖2(a)中峰值應力較低的3條直線(即變形溫度為1 000、1 050和1 100 ℃)斜率的平均值；β取圖2(b)中峰值應力較高的3條直線(即變形溫度為900、950和1 000 ℃)斜率的平均值；α可以通過式(5)求出。計算得到n/βα==0.005 026。

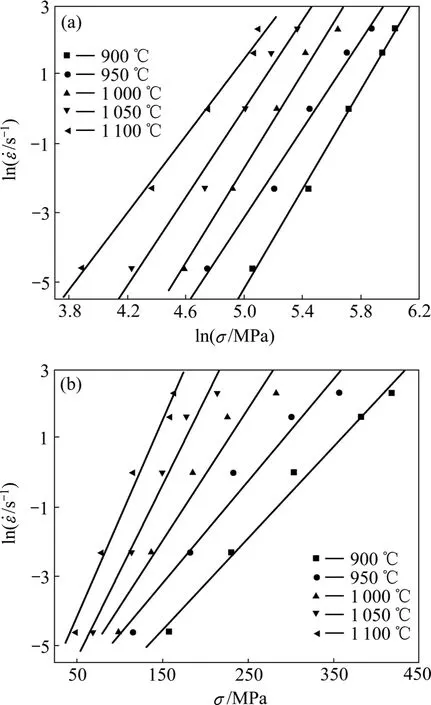
圖2 不同變形溫度下應變速率和流變應力之間的關系Fig.2 Relationship between strain rate and flow stress at different deformation temperatures∶ (a) ln—lnσ; (b)ln—σ

取峰值應力和對應溫度值，并將以上得出的α值代入式(11)，繪制 ln[sinh(ασ) ]— ln圖，n2為直線ln[sinh(ασ) ]— ln的斜率。采用最小二乘法線性回歸，得n2= 4.754 952；再將n2值代入式(5)得到一個調整后的α′值，α′=β/n2=0.006 109，將調整后的α′值重新代入式(11)和(12)，繪制相應的 ln[sinh(ασ)]— ln圖以及 ln[sinh(ασ)]—103T?1圖，如圖3和4所示。采用最小二乘法線性回歸，n3值取圖3中1 000、950和900 ℃這3條直線斜率的平均值，得到調整后的n3=4.462 888；k為直線 ln[sinh(ασ)]—T?1的斜率，k值取圖4中 5條直線斜率的平均值(1.462 364)，則Q=Rnk=527.5 kJ/mol。重復上述步驟，直至Q值變化不大時視為精確值。計算10次后，Q值基本趨于穩定值，Q=416.5 kJ/mol。

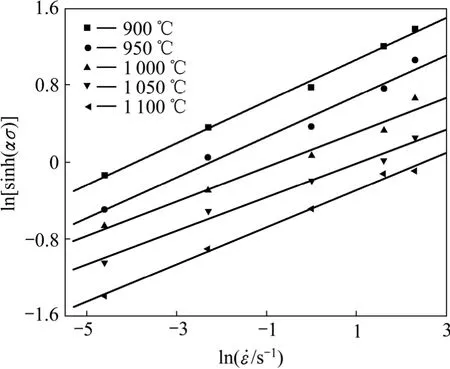
圖3 不同變形溫度下流變應力與應變速率的關系Fig.3 Relationship between flow stress and strain rate at different deformation temperatures

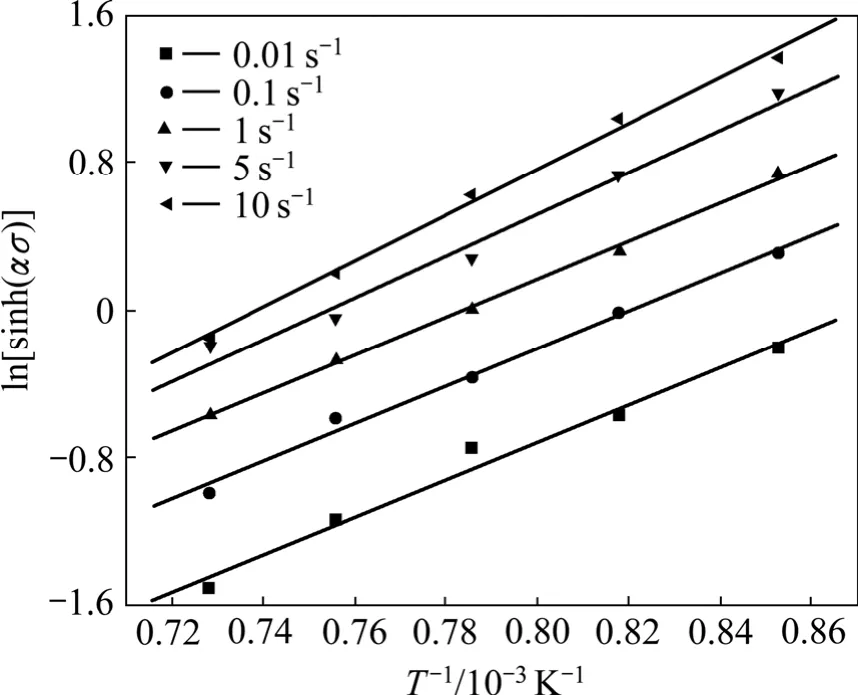
圖4 不同應變速率下流變應力與變形溫度的關系Fig.4 Relationship between flow stress and deformation temperatures at different strain rates

對式(7)求對數得：

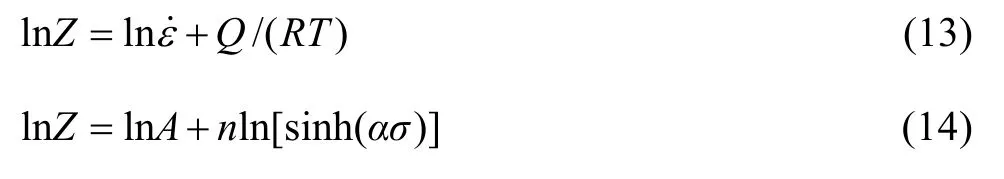
由)(σF的其他2種形式即式(2)、(3)，式(7)可表示如下：

分別對式(14)和(15)求對數得：

將以上求得的Q值及不同的應變速率和變形溫度代入式(13)，求得對應的lnZ值。將lnZ值和對應的σ值分別代入式(14)、(17)和(18)繪制ln Z—ln[sinh(ασ)]、lnZ—lnσ和lnZ—σ曲線，采用最小二乘法進行線性回歸，結果如圖5所示。圖中 ln Z—ln[sinh(ασ)]、lnZ—lnσ、lnZ—σ關系曲線的線性相關系數分別為0.988 21、0.993 43和0.968 41，可見相比較而言，lnZ—lnσ較好地滿足線性關系，將圖5(b)中的斜率和截距代入式(17)得到 lnA1=6.477 08，n=6.299 87，將其代入式(1)可得合金的流變應力方程如下：

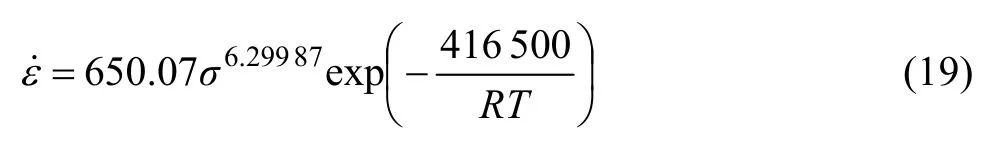
2.3 高溫壓縮過程中顯微組織的演化規律

圖6所示為不同變形條件下合金的金相顯微組織，可見在變形溫度為900 ℃、應變速率為0.01 s?1條件下，在變形的晶粒界面出現了一些細小的晶核(見圖6(a)中箭頭所指)，這些晶核即為再結晶晶核；而在變形溫度為900 ℃、應變速率為1 s?1的條件下，很難觀察到再結晶晶核(見圖6(b))。這是由于塑性變形需要一定的時間來進行，應變速率高時，變形時間短，使得動態再結晶還來不及充分發生[14?15]。在應變速率為0.01 s?1、變形溫度為950 ℃和1 000 ℃條件下，再結晶晶粒逐漸增多(圖6(c)和(d))，但在變形溫度為 1 000 ℃時，仍存在少部分未發生再結晶的變形晶粒(圖6(d)中箭頭所指)。當合金在1 050 ℃變形，此時已發生了完全再結晶，變形晶粒全部由等軸的再結晶晶粒所代替，在應變速率為1 s?1時，晶粒比較細小、均勻(圖6(e))。隨著溫度進一步升高，當變形溫度為1 100 ℃時，再結晶晶粒尺寸增大(圖6(f))，表明此時處于晶粒長大階段。

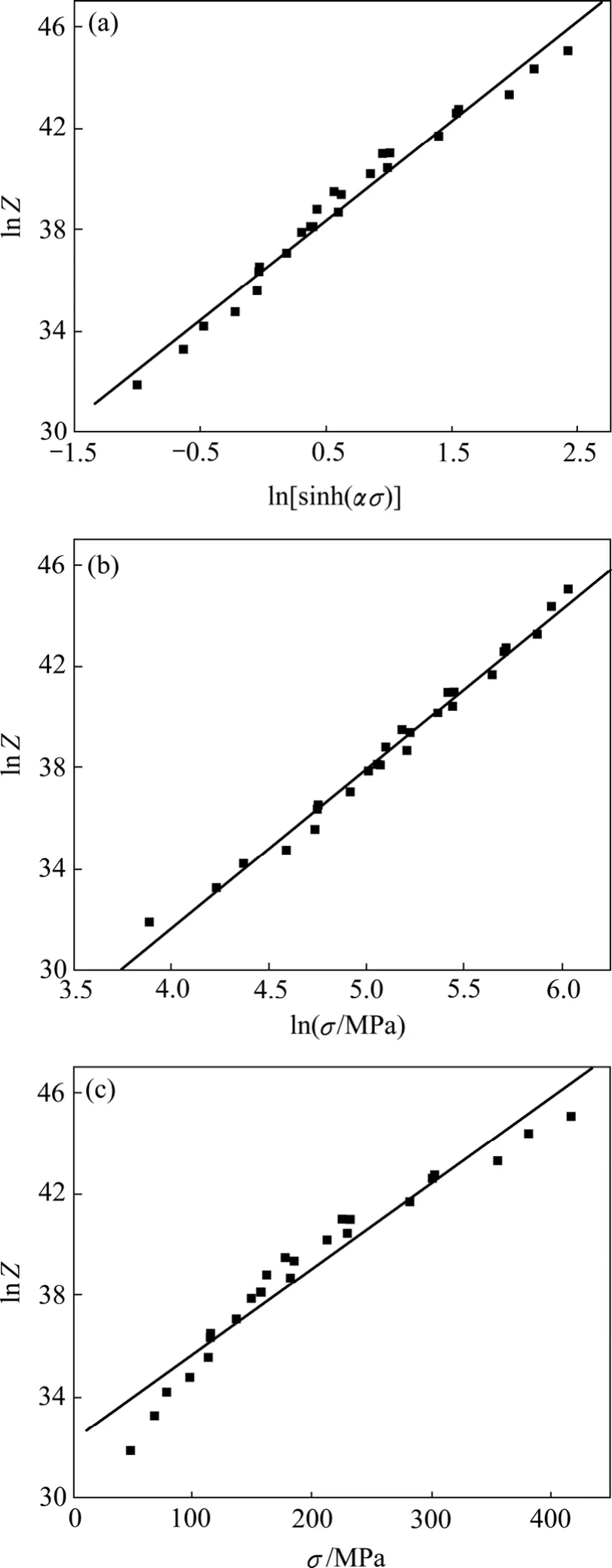
圖5 Z參數與流變應力之間的關系Fig.5 Relationship between flow stress and Zener-Hollomon parameter∶ (a) ln Z— ln[sinh(ασ) ]; (b) ln Z—lnσ ; (c) ln Z—σ

圖6 不同變形條件下合金的顯微組織Fig.6 Microstructures of specimens after being compressed under different conditions∶ (a)900 ℃, 0.01 s?1; (b)900 ℃, 1 s?1;(c)950 ℃, 0.01 s?1; (d)1 000 ℃, 0.01 s?1; (e)1 050 ℃, 1 s?1; (f)1 100 ℃, 1 s?1

3 結論

1)鎳銅合金NCu30-4-2-1高溫壓縮變形時的流變應力隨溫度的升高而減小，隨應變速率的增加而增大。流變應力σ與變形溫度T與應變速率之間滿足關系其中，變形激活能Q=416.5 kJ/mol。

2)鎳銅合金NCu30-4-2-1高溫壓縮變形時的顯微組織受變形溫度和應變速率的影響，溫度越高、應變速率越低，越有利于動態再結晶的發生。在變形溫度為1 050 ℃、應變速率為1 s?1的條件下，合金發生了完全動態再結晶，晶粒細小、均勻。

[1]PARK K H, MOHAPATRA D, RAMACHANDRA REDDY B.A study on the oxidative ammonia/ammonium sulphate leaching of a complex (Ni-Cu-Co-Fe)matte[J].Hydrometallurgy, 2007, 86∶164?171.

[2]YE Tang, HU Chuan-shun, QIN Hua, ZHU Jian.Study of corrosion behavior of Monel 400 alloy[J].Material & Heat Treatment, 2006, 35(22)∶ 36?38.

[3]GOUDA V K, SELIM I Z, HEDR A A K.Pitting corrosion behavior of Monel-400 alloy in chloride solutions[J].J Mater Sci Technol, 1999, 15(3)∶ 208?212.

[4]SINGH V B, GUPTA A.The electrochemical corrosion and passivation behavior of Monel 400 in concentrated acids and their mixtures[J].Journal of Materials Science, 2001, 36∶1433?1442.

[5]GUO Tong-xiu, LIU De-lin, YU Yang.Preparation of high silicon nickel-copper alloy NCu30-4-2-1 extrusion bars[J].Journal of Materials Engineering, 2009, 2∶ 24?28.

[6]ZHOU Yong-xin, LU Zhen-lin, ZHANG Min, ZHAO Xi-cheng,FAN Zhi-kang.Study on the tribological behavior of Monel alloy[J].Ordnance Material Science and Engineering, 2004,27(5)∶ 24?27.

[7]YANG Zhi-jun, LI Xian-min, WANG Zeng-min, LI Lin.Investigation on the behavior of silicon in Ni-Cu-Fe-Mn-Si alloy[J].Rare Metals and Engineering, 1997, 26(5)∶ 47?50.

[8]KOU Lin-yuan, JIN Neng-ping, ZHANG Hui, HAN Yi, WU Wen-xiang, LI Luo-xing.Flow stress behavior of 7150 aluminum alloy during hot compression deformation at elevated temperature[J].The Chinese Journal of Nonferrous Metals, 2010,20(1)∶ 44?46.

[9]SELLARS C M, MCTEGART W J.On the mechanism of hot deformation[J].Acta Metal, 1966, 14∶ 1136?1138.

[10]MCQUEEN H J, YUE S, RYAN N D, FRY E.Hot working characteristics of steels in austenitic state[J].J Mater Process Technology, 1995, 53(1)∶ 293?310.

[11]MCQUEEN H J, FRY E, BELLING J.Comparative constitutive constants for hot working of Al-4.4Mg-0.7Mn (AA5083)[J].Journal of Materials Engineering and Performance, 2001, 10(2)∶164?172.

[12]HU Hui-e, YANG Li, ZHEN Liang, SHAO Wen-zhu, ZHANG Bao-you.Relationship between boundary misorientation angle and true strain during high temperature deformation of 7050 aluminum alloy[J].Transactions of Nonferrous Metals Society of China, 2008, 18(4)∶ 795?798.

[13]ZENER C, HOLLOMON J H.Effect of strain-rate upon the plastic flow of steel[J].J Appl Phys, 1944, 15(1)∶ 22?27.

[14]BLUM W, ZHOU Q, MERKEL R, MCQUEEN H J.Geometric dynamic recystallization in hot torsion of Al-5Mg-0.6Mn[J].Mater Sci and Eng A, 2002, 205∶ 23?30.

[15]DOHERTY R D, HUGHES D A, HUMPHRYS F J.Current issues in recystallization∶ A review[J].Mater Sci and Eng A,1997, 238∶ 217?274.