《用窮舉法設計程序》教學設計

☆高騰

一、教學目標

知識與技能：了解什么是窮舉法，了解運用窮舉法設計算法的基本過程，能根據具體問題運用窮舉法解決簡單問題。

過程和方法：通過對實際問題的窮舉程序實現過程的觀察，發現和歸納窮舉算法的一般規律，發展歸納思維，培養獨立思考與自主探究的學習能力。

情感與價值目標：了解算法和程序設計在計算機解決問題過程中的重要性，體驗將算法變為程序的過程，享受計算機解決問題的快樂，通過對實際問題的解決，體驗算法在實際生活中的廣泛應用，激發對算法與程序設計的求知欲，形成積極主動的學習態度。

教學重點、難點：

重點：根據具體問題的具體要求來使用窮舉法設計算法，并編寫相應程序。

難點：學生歸納思維的培養。

二、教學過程設計

1.創設情境，激趣引入

教師活動：我們現在先來回答一道搶答題：甲、乙、丙高考結束后在一起討論。甲說：“我肯定能考上重點大學。”乙說：“重點大學我是考不上了。”丙說：“要是不論重點不重點，我考上大學肯定沒問題。”放榜結果表明，3人中考上重點大學、一般大學和落榜的各一人，并且他們3人的預測結果只有1個是對的。那么，3人中誰考上重點大學，誰考上一般大學，誰沒考上呢？

（設計意圖：之前的課堂舉的都是數學例子，為防止學生“審美疲勞”故采用了邏輯實例來激發學生的學習興趣，調動學生學習積極性，并為下面的探究創造氛圍。）

2.展示問題，引入課題

教師活動：（1）分析人腦解決問題過程并和學生共同完成下表。（2）引入用程序設計來解決問題，要求學生給出算法流程。

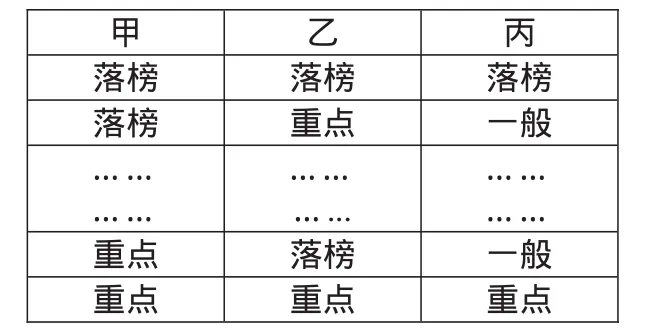
（設計意圖：讓學生了解人腦是怎么用窮舉法來解決問題的，再過渡到通過窮舉法編程來解決問題。）

3.師生共同探究

教師活動：逐句分析調試以下程序。

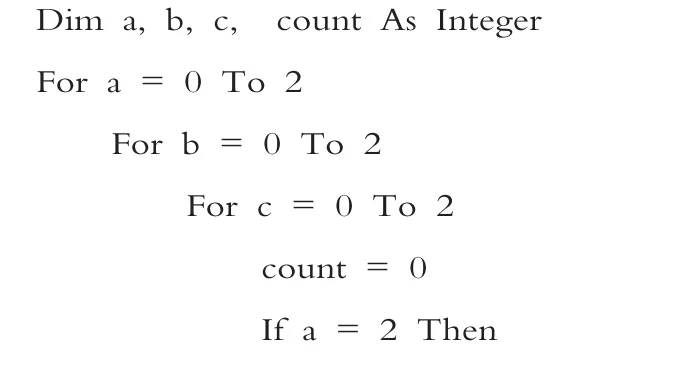
教師引導：在分析了如上程序后，你能發現什么？

學生發現：（1）變量a,b,c存放的是甲、乙、丙的高考結果，分別用0,1,2來表示落榜、一般大學、重點大學3種狀態。（2）變量count存放的是3人猜測的結果正確數。（3）此程序的功能是列出3個人所有考試結果，如果滿足各不相同且只有1人猜對就輸出。

教師總結：此程序的特點是將求解對象的所有可能性都列舉出來，然后一個個進行驗證是否滿足給定條件，若不滿足則淘汰，滿足則輸出。當所有對象都被篩選完后，問題即得到解決。這種算法就是窮舉法。

（設計意圖：給學生足夠的時間觀察，學生思考這個過程是無法替代的，最后在教師的引導下總結出窮舉法的規律。）

4.知識鞏固深化

教師活動：要求學生用窮舉法來解決“雞兔同籠”問題。雞和兔在一個籠里，共有40個頭，100條腿，問雞有幾只，兔有幾只？給出以下部分程序代碼，與學生共同補充完整。

學生活動：回答問題并對比與自己所寫的程序有何不同。

教師引導：（1）上面的程序是否存在不盡如人意的地方，你能修改一下嗎？（2）通過以上2個窮舉法程序解決問題，你們能總結出一些規律嗎？

學生回答：a,b的窮舉范圍超過需要，可以適當減少以提高程序運行效率。

學生歸納：（1）確定變量個數；（2）確定窮舉范圍，用for循環實現；（3）窮舉規則用if語句實現；（4）盡量減少窮舉范圍以提高效率。

（設計意圖：之前解析法已經有接觸到此例，從學生熟悉的例子入手，學生可以在觀察過程中發現、歸納并解決問題，并對比窮舉法與解析法的差異。）

5.課后實踐

問題1：京城某商鋪被盜，抓了甲、乙、丙、丁、戊5個嫌犯，可是不知道其中哪幾個人是真正的罪犯。不過有確鑿的證據表明：（1）如果甲參與了作案，則乙一定也會參與；（2）乙和丙兩人中只有一人參與了作案；（3）丙和丁要么都參與了作案，要么都是無辜的；（4）丁和戊兩人中至少有一個人參與作案；（5）如果戊作案，那么甲和丁一定也參與了作案。究竟哪些人才是真正的罪犯？

問題2：從1-9這9個數字中取6個填入下面式子中，使等式成立，每個數字每次只能用1次，你能組成多少個等式？

（ ）*（ ）（ ）=（ ）（ ）（ ）

（設計意圖：學生在課堂上已經完成了觀察、發現、歸納這幾個步驟，最后的作業則驗證其是否能將所學知識應用到求解實際問題當中，即要求學生應用自己在課堂上歸納總結出來的規律對問題進行求解。）

三、課后反思

本節課有幾點收獲。

（1）達成率高。學生在掌握了窮舉法設計程序的方法后，有運用技術來解決實際問題的迫切愿望，對于課后作業的完成有很大的積極性。

（2）學生分析問題、解決問題的能力得到較大幅度的提高，能將課堂歸納總結到的規律運用到實際當中。比如：課后作業2，學生不僅能合理運用信息技術課堂所學知識來減小窮舉范圍，甚至還有學生根據排列組合計算出最少的窮舉次數，只是因為編程知識所限而無法實現。

（3）采用邏輯題作為課堂實例使得學生對程序設計又有了新的理解，學編程并非只能解決數學問題，不僅活躍了課堂，也留給筆者一個深深的思考——我們究竟需要什么樣的教材。

當然本節課也存在不足。本課原本是想全采用邏輯題作為實例講解的，但是邏輯題作為實例雖好卻也存在不足——其窮舉范圍太小而容易使學生忽視窮舉范圍影響程序效率這一知識點。如果對其進行修改則又容易導致程序太繁雜不利于學生理解。所以，課堂實例采用了雞兔同籠這道題作為對知識點的補充與鞏固。

[1]張麗.《用窮舉法解決問題》教學設計[J].信息技術教育,2007,(6).

[2]余錦波.邏輯的藝術[M].重慶:重慶大學出版社,2011,1.

[3][50]信息技術教材編寫組.信息技術[M].福州:福建教育出版社,2012.

[4]王東方.我的計算機繪圖課里有故事[J].中小學信息技術教育,2004,（1）.