一個(gè)向量旋轉(zhuǎn)問題的探討

●

(大化縣高級(jí)中學(xué) 廣西大化 530800)

一個(gè)向量旋轉(zhuǎn)問題的探討

●覃志根

(大化縣高級(jí)中學(xué) 廣西大化 530800)

向量是高中數(shù)學(xué)的重要內(nèi)容，它具有幾何與代數(shù)的雙重屬性，與函數(shù)、三角函數(shù)、圓錐曲線等內(nèi)容有著“親密”的關(guān)系.在近幾年的高考試題中，向量與函數(shù)、三角函數(shù)、圓錐曲線等內(nèi)容結(jié)合的題目越來越多，可以說“到處可以見到它們的影子”.解決此類問題的方法靈活多樣，本文以2012年安徽省數(shù)學(xué)高考的一道選擇題為例，研究探討向量旋轉(zhuǎn)問題的解法.

( )

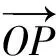
(2012年安徽省數(shù)學(xué)高考理科試題)

解法1根據(jù)定義和三角求值.

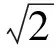
解法2估算.

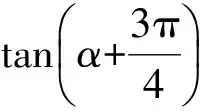
解法3利用向量的夾角公式和模長(zhǎng)公式，結(jié)合待定系數(shù)法．

設(shè)Q(x,y)，則

即

x2+y2=100.

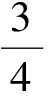
即

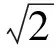
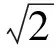
解法5由題意，知

設(shè)點(diǎn)Q(x,y)，則

解得

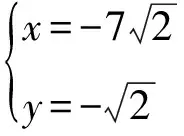
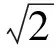
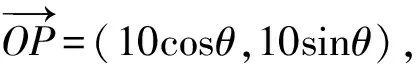
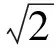
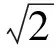
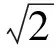
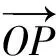
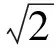
因此

從而直線OQ的傾斜角為

即

|OQ|2=|OP|2=100，

所以

x2+y2=100.

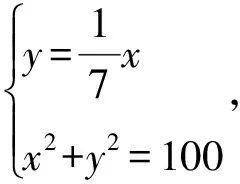
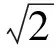
即

設(shè)Q(x,y)，則

本題入口寬，方法多，活而不難，注重通性通法，淡化特殊技巧，突出對(duì)學(xué)生靈活運(yùn)用知識(shí)能力的考查.解法1利用定義和三角函數(shù)求值；解法2注重對(duì)問題的估算，進(jìn)行排除運(yùn)算；解法3利用向量的夾角公式和模長(zhǎng)公式，結(jié)合待定系數(shù)法求解；解法5充分利用向量“數(shù)”的特征，體現(xiàn)了方程思想的應(yīng)用；解法6將向量的旋轉(zhuǎn)與三角函數(shù)的定義結(jié)合起來，體現(xiàn)了三角函數(shù)與向量的內(nèi)在聯(lián)系；解法7充分利用了向量加減運(yùn)算的平行四邊形法則，體現(xiàn)了數(shù)形結(jié)合思想的應(yīng)用；解法8、解法9、解法10分別利用復(fù)數(shù)、參數(shù)方程、極坐標(biāo)等知識(shí)，將所求問題賦予了新的含義.

上述各種解法，是對(duì)所給問題多角度觀察、聯(lián)想、思考的結(jié)果.本題讓我們又一次深刻體驗(yàn)到：高考題中蘊(yùn)含著基本的數(shù)學(xué)思想方法，一題存在多種解法，具有靈活多樣性的特點(diǎn).