一道簡潔優美賽題的多解與引申

●

(湖州市第五中學 浙江湖州 313000)

一道簡潔優美賽題的多解與引申

●計惠方李明妍

(湖州市第五中學 浙江湖州 313000)

2013年浙江省高中數學競賽有這樣一道簡潔優美的試題：

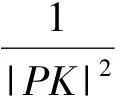
1 一般情形

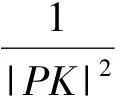
2 多種證法

賽題除參考答案提供的常規證法外，還有如下簡便易行的證法：

分析1由于直線PQ的斜率可以不存在但不為0，為避免對斜率進行討論，設直線為x=ky+m．

證法1設直線PQ的方程為

x=ky+m,P(x1,y1),Q(x2,y2)．

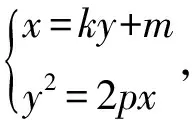
y2-2pky-2pm=0,

于是

y1+y2=2pk,y1y2=-2pm.

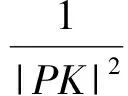
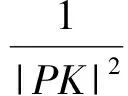
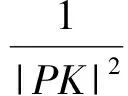
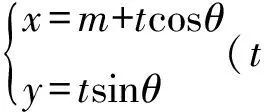
證法2設直線PQ的參數方程為

其中t為參數，θ為直線的傾斜角，此時θ∈(0,π)，且點P,Q對應的參數為t1,t2.將直線PQ的參數方程代入拋物線y2=2px(p≠0),得

sin2θ·t2-2pcosθ·t-2mp=0(sinθ≠0),

則

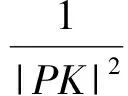
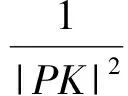
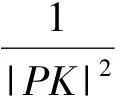
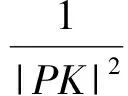
又當點P→O時，

|KP|→|KO|=m,|KQ|→+∞,

從而

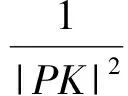
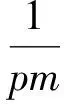
證法3設直線PQ的方程為

x=ky+p,P(x1,y1),Q(x2,y2)．

y2-2pky-2p2=0,

則

Δ=4p2k2+8p2>0,

y1+y2=2pk,y1y2=-2p2.

又

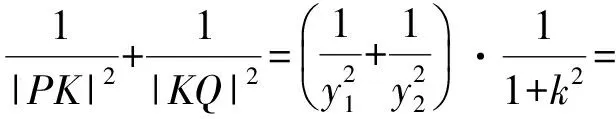
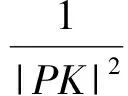
3 變化引申

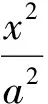
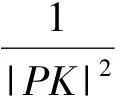
當PQ⊥x軸時，設P(m,n),則Q(m,-n).因為點P,Q在橢圓上，所以

即

于是

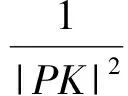
當PQ與x軸重合時,

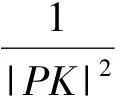
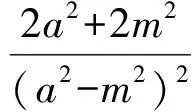
根據假設有

解得

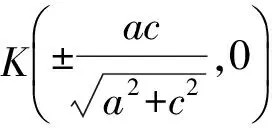
證明當直線PQ與x軸不重合時，設直線PQ的方程為

P(x1,y1),Q(x2,y2).

(b2k2+a2)y2+2mkb2+b2m2-a2b2=0,

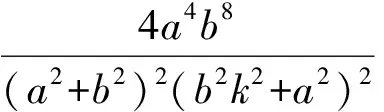
從而 (y1+y2)2-2y1y2=

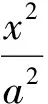
證明可仿引申1.

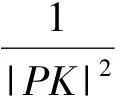
當PQ⊥x軸時，設P(m,n),則Q(m,-n).因為點P,Q在雙曲線上，所以

即

于是

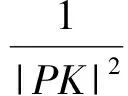
當PQ與x軸重合時，

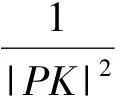
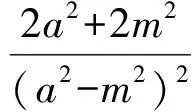
根據假設有

解得

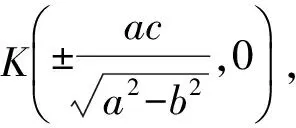
證明可由感興趣的讀者完成.

[1] 計惠方.例談課本知識與高考試題的對接[J].中學教研(數學),2012(1)：45-47.

[2] 計惠方，蔡穎.聚焦由直線系產生的定值問題[J].中學生數學(上),2013(1)：24-25.