形式化與非形式化在課堂教學中的融合演繹

●

(樂清中學 浙江樂清 325600)

形式化與非形式化在課堂教學中的融合演繹

●徐建榮

(樂清中學 浙江樂清 325600)

高中數學新課程從總體上來說，是為學生學習必需的、有用的數學，刪減了不必要的、陳舊的數學內容，一定程度上減少了學生的學習壓力，從出發點來說值得肯定．其減少了形式化數學的結果、證明等，大大加深了感性認知等非形式化手段在數學教學中的運用，但如何把握這兩者的完美融合仍然是教學的一個難題．

近幾年浙江省關于高中數學新課程進行了很多相關的學習、交流，筆者也參與觀摩了很多的公開課.如今的公開課與時俱進，更多關注學生的“參與度”、課堂的“新鮮感”等教學理念滲透.辯證來看:既不能過于強調“參與度、情境和探究”，也不能一味保守,總是采用傳統的“啟發式教學”．現實中，如今的常態課還走在過于形式化、啟發式教學的誤區，而公開課卻行走在完全非形式化、情境式教學的誤區．結合當今的高中數學教學，筆者認為：高中數學中“形式化的結果”仍比較常見(諸如函數的概念、平面向量基本定理等)，而“非形式化的數學”往往能讓學生對數學知識的表象理解和記憶，但卻無法指導學生到達數學概念的彼岸——窺視其規律與本質(如數形結合以形輔數、函數與方程思想等)．在新課程理念下，就如何結合形式化與非形式化的數學教學，筆者有一些不成熟的想法與大家分享．

1 概念對比

形式化和非形式化一直是數學教學中的兩大產物，其特點主要圍繞下面5點進行界定和區分：

表1 形式化與非形式化的數學教學

2 融合教學

《普通高中數學課程標準》明確指出：在數學教學中，學習形式化的表達是一項基本要求，但是不能只限于形式化的表達，要強調對數學本質的認識，數學的現代發展也表明，全盤形式化是不可能的，因此，高中數學課程應該返璞歸真，把數學的學術形態轉化為學生易于接受的教育形態[1]．

“數學形式化”猶如舊版教材一直提倡的“啟發式教學”，而“非形式化”恰恰猶如新課程所一直提倡的“情境式教學”，我們不能說“數學形式化”完全不符合高中學生的認知，好比完全否定“啟發式教學”毫無優點一樣，也沒有任何證據說明“非形式化”就能讓高中生更透徹地理解數學概念、定理等，好比“情境式教學”就遠比“啟發式教學”優秀，有種高高在上的感覺一樣[2]．

張奠宙教授說過：數學教育要注重認知，淡化形式，但是不能丟了形式化——淡化(對中學生而言)并非完全否定，只是小學生、中學生、大學生各種年齡階段的學生都要按照不同形式化程度來教學．筆者認為，對高中生數學課堂教學應該介于形式化和非形式化之間，即適度的形式化更符合高中生的認知心理．

3 特點分析

形式化是數學特有的產物，從舊的人教版教材開始，形式化一直是中學數學的特點，似乎沒有形式化，數學就不是數學．劉紹學教授語：以往的中學課堂，教師首先給學生介紹一個數學的定理，然后進行嚴密的證明，進而對定理進行幾點注意，最后使用定理解決數學問題．這種數學課是形式化比較明顯的，在以往看來，這樣的數學教學有幾個好處：

(1)數學知識的傳授連貫，教師教學比較方便；

(2)數學定理的證明比較嚴密，使得學生心服口服；

(3)數學知識基本一步到位，在某個定理處進行變式教學、反復演練，熟悉為止．

但是形式化的數學漸漸顯現出不足，主要有：

(1)對高中生而言，是不是也要學那么形式化的數學呢？反之，如果淡化一點，會不會有更好的教學效果？

(2)是不是每個人將來都會用到這么形式化的數學呢？

(3)數學都要追求形式化，是不是太費神費力？

隨著新課程改革的不斷深入，作為教材主導地位的形式化數學漸漸走下神壇，取而代之的是新教材，新教材較明顯地弱化了形式化的數學在高中數學中的地位．因此，“如何融合兩者，如何在教學中進行完美的滲透”是教師教學的一種境界.下面以筆者觀摩的一堂公開課“數學歸納法(第一課時)”為例進行分析說明.

4 教學案例

4.1 非形式化階段——創設情境，思考問題

探究1人工探索

探究2智能探索

結合程序語言，給出如圖1所示的框圖：

圖1

探究3可行性探討

由學生來探討這個智能探索是否可行，能否達到證明的目的．

設計意圖由學生熟悉的3個連續探究引入本節課，符合學生的認知規律看似沒有給出數學歸納法，實質上已經讓學生從潛意識中接觸到了數學歸納法的適用范圍，這種探究式的教學可以讓學生親臨數學歸納法的形成過程，逐漸感受數學歸納法的必要性與必須性，加深對概念的理解，并且在一次次的探究收獲中慢慢接觸數學歸納法的關鍵，尤其在首次接觸中顯得尤為重要．

4.2 形式化初步階段——層層遞進，誘發思維

在上述探究的基礎上，學生明白以上辦法都不能證明，因此接下來在“非形式化階段”的基礎上繼續思考和提煉.這個提煉的過程也許對于學生來說會比較抽象，但必不可少，這個過程需要教師的正確點撥和引導.經歷了這個過程，學生就會對數學歸納法的基礎和依據有深刻的理解．

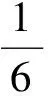
直面無限，我們真的束手無策？接下來通過類比等差、等比數列完成探究4.

探究4類比探索

表2 類比等差、等比數列

由表2得到探究收獲：類比數列中處理無限的方法，可以得到一種全新、巧妙的證明方法．

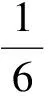
設計意圖通過上述幾個問題及探究，已經明確給出了數學歸納法的過程，教師以等差、等比數列對應為學生的“最近發展區”，抽象得出證明一個命題成立的過程.這正是一種類比推理的思想和建構的過程．通過對一個具體問題的深入研究，得到了一種新的數學概念，也得到了數學歸納法的本質．

4.3 形式化與非形式化融合——明確概念，活學活用

在上述基礎上，進一步思考：

問題3新的證明方法適合于哪種題型？

問題4你能總結出新證明方法的解題步驟嗎？

由此給出本節課的課題：數學歸納法，同時很自然地給出了數學歸納法的解題步驟．

問題5你能用數學歸納法來解析多米諾骨牌游戲嗎？

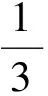
設計意圖在“非形式化階段”到“形式化階段”的基礎上，通過抽象的概況，給出了數學歸納法的適用范圍和明確的解題步驟，并且及時對關鍵性步驟、易錯知識點進行點撥，使學生成功地完成了質的飛躍．

4.4 形式化最終階段——錯誤辨析，思維升華

(1)與數學歸納法有關的美麗誤會：費馬質數(當p是質數時，22p+1是質數)直到費馬去世后67年，著名的數學家歐拉才證明了這個命題的錯誤性．

(2)有人聲稱證明了“所有的奇數都是2的倍數”．

最后進行課堂小結，用3個英語單詞總結——數學歸納法學習的“why？where？what？”來結束本堂公開課．

設計意圖在學生已經掌握數學歸納法本質及步驟的情況下，給出反例辨析：第1個反例缺遞推；第2個反例缺基礎，由此進一步讓學生理解2個步驟缺一不可．最后的3個單詞進一步幫助學生進行反思：為什么要用數學歸納法，什么時候用數學歸納法，怎么用數學歸納法．整堂課如行云流水一般把形式化和非形式化自然融合，通過對一個具體題目的層層遞進研究，得到了本節課對概念學習的從形象到抽象的過程，是形式化數學用非形式化手段完美演繹的一節公開課．

5 教學思考

高中數學課堂教學比較合適的方式，是有機融合形式化和非形式化的運用，將啟發式教學與情境式教學恰當地整合，其主要目的是通過整合創新教學模式，使得以學生為主體的教學理念設計不是一句空話，其優點在于充分發揮學生的參與性，無論是后進生還是優等生，在其各自不同的范圍之內(大多數學生更容易接受感性非形式化的數學，少數則比較容易把握形式化的數學結果)對數學知識和問題的不同層次進行不同程度的涉及，真正落實新課程重要的開發理念：注重對數學知識形成過程的學習，淡化過于形式化的結果與證明．

筆者最后想說，高中數學課堂教學有很多方面值得我們關注，筆者從“數學歸納法”案例入手，分享了如何進行有機融合非形式化和形式化的教學策略.在教學時，教師要注意對高中學生采用的教學方法，既不能一味“情境化”(過于直覺、感官)，也不能“形式化、啟發式教學”過度.只有2條腿走路，才能使學生能體驗和感悟到數學思維的理性精神，才能做到與時俱進的有效教學．

[1] 羅展華.高中數學教學中形式化與非形式化表現特征[J].中學教研(數學),2009(4):12-14.

[2] 張煥明.淺論素質教育觀下的數學課題設計[J].中學教研(數學),2002(4)：8-11.

[3] 張繼紅.創新教育下中學數學課堂教學模式研究[D].長春：東北師范大學，2002.

[4] 涂榮豹.論數學活動的過程知識[J].數學教育學報,2002(11)：9-13.