云來山更佳 云去山如畫——對2013年浙江省數學高考理科第16題的多角度探究
●
(杭州市第十一中學 浙江杭州 310014)
云來山更佳云去山如畫——對2013年浙江省數學高考理科第16題的多角度探究
●蔡小雄陳發志
(杭州市第十一中學 浙江杭州 310014)
前蘇聯數學教育家奧加涅說過:很多習題潛在著進一步擴展其教學功能、發展功能和教育功能的可能性.很多數學問題本身看似平淡無奇,但若能挖掘其內涵,適當變化,常常會有意想不到的收獲.2013年浙江省數學高考理科第16題就是這樣一道呈現形式簡潔優美、設問方式平實無奇,但內在積淀深厚、引人入勝的經典好題.通過對這道題目的解法探究、變式拓展、背景揭示,我們會發現一個包羅數學核心本質的大世界,會發現數學橫縱遷移的美妙變化!
1 立足本質,探尋多種解法
本題以解三角形為載體,以邊角關系的轉化為突破口,考查學生對三角函數、解三角形等知識的掌握程度.雖然僅是一道填空題,但題目立意新穎、呈現獨特、內涵豐富、能力要求高.從閱卷情況來看,該題是全卷得分率最低的一道題.很多考生拿到題目后不知從何入手,或者僅停留于問題表面“給角求角”的層次,不能進行邊角關系的轉化,或者對中點這一條件無法進行突破.通過深入分析,不難發現只要準確把握問題本質,我們可以從不同的角度入手得到多種解法.
1.1 利用坐標法
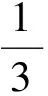

圖1
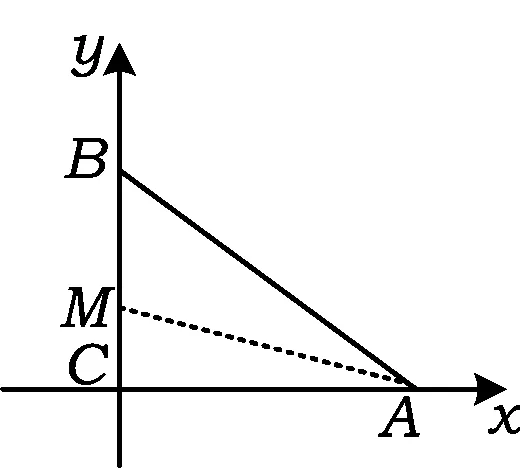
解法1建立如圖1所示的平面直角坐標系,設A(a,0),B(0,2),M(0,1),則
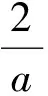
即
tan∠BAM= tan(∠BAC-∠MAC)=

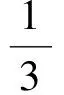

即

亦即

解得

從而

故

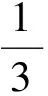
1.2 利用三角函數公式
本題如果從探究角關系進行分析,不難發現∠BAM+∠CAM=∠BAC,因此可以從三角函數兩角和與差的正(余)弦公式入手.

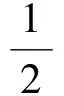
將AC=AMcos(α-β)代入式(1),化簡可得

同理,由S△ABM=S△ACM可得
式(2)+式(3),得
sin(2α-β)=1.
注意到α,β的范圍,得
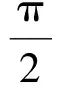
即
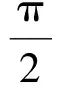
因此
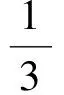


1.3 利用余弦定理
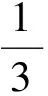
解法3設AM=1,sin∠CAM=k(0 在△ABM中,由余弦定理,得 點評題中條件所給的是角的正弦值,不難得到余弦值,而余弦定理正是轉化邊角關系的核心“媒介”,從邊角關系的本質著手很容易找到突破口. 1.4 利用正弦定理 題目所給的條件是關于∠BAM的正弦值,由此聯想利用正弦定理突破.而對于sin∠BAM可以通過構造一個直角三角形表示出相應的邊. 圖2 解法4如圖2,過點B作BD⊥AB交AM的延長線于點D.令BD=1,AD=3,BM=x,AM=y,則 sin∠BMD= sin∠AMC= 在△BDM中,由正弦定理知 即 (4) 又在Rt△ACM中,由 AM2=CM2+AC2, 得 y2=x2+8-4x2=8-3x2, 代入式(4),得 解得 故 點評本題的關鍵是2個未知量如何通過構造方程組來求解:(1)在△BMD中利用余弦定理得到一個方程;(2)在Rt△ACM中運用勾股定理得到另一個方程. 1.5 利用向量知識 (a-b)·b=0, 從而 a·b=|b|2=y2. 因為 從而 x2=3y2, 即 故 點評向量是溝通數與形的完美“結合體”,在三角函數、解三角形、立體幾何、解析幾何中都有向量的身影.尤其是在遇到代數運算較復雜的問題時,利用向量這一工具能起到事半功倍的效果. 1.6 利用三角形相似 圖3 從而 x2y2=x2+y2. 又在Rt△ABC中,4x2+y2=9,兩式消去y,得 x2(9-4x2)=x2+9-4x2, 解得 即 故 點評解法6與解法4有著異曲同工之處,不同之處在于一個是通過正弦定理得到方程,而本題是通過三角形相似得到方程. 1.7 利用勾股定理 圖4 解得 從而 點評本題的關鍵是如何用CM的長x表示出各邊長,并在此基礎上利用勾股定理輕松求得. 通過一道數學試題,若能引導學生從不同方向、不同角度、不同方位進行思考,可以激活學生的思維能力,幫助學生訓練基本技能、基本方法,更重要的是可以開闊學生的思維,培養學生思維的靈活性、發散性、廣闊性和深刻性.本題也可以從“變特殊到一般、變已知為未知、變定值為變量”這3個角度進行變式拓展,從而進一步揭示問題的本質. 2.1 變特殊為一般 圖5 解建立如圖5所示的平面直角坐標系,設A(a,0),B(0,1),M(0,λ),則 從而 tan∠BAM= tan(∠BAC-∠MAC)= 即 化簡得 解得 2.2 變已知為未知 變式2在△ABC中,∠C=90°,點M是BC的中點.若sin∠BAC=m,則sin∠BAM=______. 由余弦定理,知 2.3 變定值為變量 變式3在△ABC中,∠C=90°,點M是BC的中點.若BC=2,AC=a(a>0),則sin∠BAM的最大值是______. 解建立如圖1所示的直角坐標系,設A(a,0),B(0,2),M(0,1),則 從而 教材是高考命題的源泉,高考命題的主要思想就是“源于教材,又不拘泥于教材”.因此,研究高考試題的設計背景,有利于揭示問題的本質.變式3的原型是人教版《數學(必修5)》第101頁B組的第2題,原題如下: 例2樹頂A離地面am,樹上另一點B離地面bm,在離地面cm的C處看此樹,離此樹多遠時看A,B的視角最大? 當然,還可以進一步探究問題的幾何背景如下: 圖6 已知線段BC的中點為M,直線l經過點C且垂直于BC,點A在直線l上運動,則當且僅當AC2=CM·CB時,∠BAM取得最大值. 分析如圖6,以AB為弦做動圓O,圓O與直線l有交點,記其中一個交點為A,則∠BAM為弦AB所對的圓周角,故要讓∠BAM最大,則圓O的半徑要最小.不難發現當AC與圓O相切時,半徑最小,即∠BAM最大,又由圓的切割線定理知AC2=CM·CB. 知道了這個幾何背景,可輕松解決例1: 通過對問題全方位、多角度、深層次的思考與探索,以不同知識內容為切入口,探索出不同的解決方法,有利于調動學生的學習積極性,激發求知欲,引起興趣,也有利于發展智力,克服思維定勢的束縛,形成創造性、發散性思維的源泉,從而讓問題在解決過程中創新不斷、驚喜不斷!
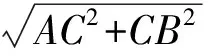

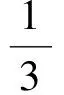
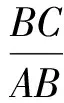




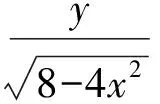

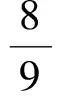
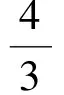
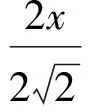



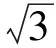

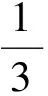

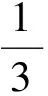



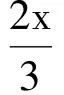
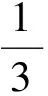





2 變式拓展,探究問題本質


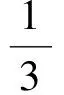

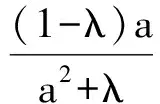



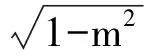
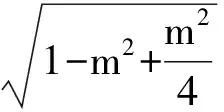
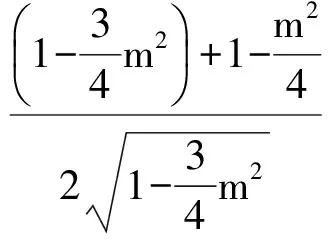

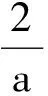
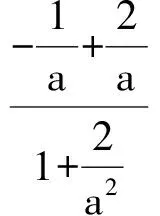

3 追本溯源,揭示問題背景