歷經(jīng)三重境界探究橢圓性質(zhì)的一個(gè)案例

● ●

(寧波市第二中學(xué) 浙江寧波 315000) (鄞州區(qū)教育局教研室 浙江寧波 315100)

歷經(jīng)三重境界探究橢圓性質(zhì)的一個(gè)案例

●任偉芳●江一鳴

(寧波市第二中學(xué) 浙江寧波 315000) (鄞州區(qū)教育局教研室 浙江寧波 315100)

高中數(shù)學(xué)課程標(biāo)準(zhǔn)指出：“高中數(shù)學(xué)課程應(yīng)力求通過各種不同形式的自主學(xué)習(xí)、探究活動(dòng)，讓學(xué)生體驗(yàn)數(shù)學(xué)發(fā)現(xiàn)和創(chuàng)造的歷程，發(fā)展他們的創(chuàng)新意識(shí)．”筆者在備高三復(fù)習(xí)課時(shí)，發(fā)現(xiàn)一個(gè)探究橢圓性質(zhì)的題目，通過此題可以引導(dǎo)學(xué)生從一個(gè)普通數(shù)學(xué)問題出發(fā)，層層推進(jìn)，自主探索，合作交流，進(jìn)而領(lǐng)悟數(shù)學(xué)思想方法．為此，筆者以該題為引子精心編制了一個(gè)“探索橢圓的一個(gè)性質(zhì)”的教學(xué)設(shè)計(jì)，并在教研活動(dòng)中進(jìn)行了展示，獲得廣泛好評(píng)．下面是這堂探究課的教學(xué)片斷和課后思考，供大家參考．

1 教學(xué)片段實(shí)錄

(2009年遼寧省數(shù)學(xué)高考理科試題)

說明課前預(yù)習(xí)作業(yè)要求：(1)用盡可能多的證法來證明；(2)如果移動(dòng)點(diǎn)A會(huì)改變直線EF的斜率，那么直線EF的斜率與點(diǎn)A的哪個(gè)值有關(guān)；(3)能否把這個(gè)結(jié)論推廣到拋物線和雙曲線上.

片段1不畏浮云遮望眼,只緣身在最高層

師：預(yù)習(xí)作業(yè)同學(xué)們準(zhǔn)備得很充分，4位同學(xué)分別用直接法、方程組法、參數(shù)法和點(diǎn)差法來證明，這4種證法都很精彩．盡管題目像“雄關(guān)漫道真如鐵”，同學(xué)們還是用多種解法把它“從頭越”．現(xiàn)在我們已處在題目思路方法的“最高層”，但不要被“浮云遮望眼”，力圖抓住問題的本質(zhì)，去猜想、拓展、引申和類比，探究出新的問題．想一想：直線EF的斜率值與點(diǎn)A的哪個(gè)值有關(guān)系？

生1：直線EF的斜率與過點(diǎn)A的橢圓切線斜率是互為相反數(shù)．我是用量角器通過量直線的傾斜角驗(yàn)證得到的，但是還沒有證明出來．

生2：這個(gè)結(jié)論我是猜想得出．

師：你是怎樣猜想出來的？

生2：只要把如圖2的橢圓變成特殊情形圓，如圖1所示，∠1=∠E+∠4，∠2=∠3+∠5，而∠1=∠2，因此∠4=∠5.類比到圖2得：直線EF的斜率與過點(diǎn)A的橢圓切線斜率是互為相反數(shù)．

圖1 圖2

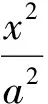
師：通過觀察由特殊情形出發(fā)，類比猜想得到一般結(jié)論是科學(xué)研究的一種有效方法,但還要嚴(yán)格證明．

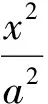
從而

設(shè)kAE=k,則kAF=-k.又點(diǎn)A(x0,y0)在橢圓上,得

從而

(b2+a2k2)x2+2a2k(y0-kx0)x+

a2(y0-kx0)2-a2b2=0.

記E(x1,y1)，F(xiàn)(x2,y2)，則

同理可得

于是

又因?yàn)閥2-y0=-k(x2-x0)，y1-y0=k(x1-x0),

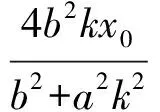
從而

又

故

kEF+kAQ=0.

師：對(duì)于一個(gè)命題成立自然會(huì)想到它的逆命題是否成立呢？

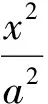
證明與結(jié)論1類似．

結(jié)論1作為橢圓性質(zhì)的基本定理，進(jìn)而又得到以下結(jié)論：

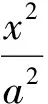
生4：根據(jù)△TAF∽△TEA，不難得到以下結(jié)論：

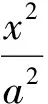
片段2行到水窮處，坐看云起時(shí)

師：橢圓也有類似于圓的性質(zhì)的確令人驚奇，似乎我們已經(jīng)到了“水窮處”了，但同學(xué)們思考一下：橢圓除了有“切割線定理”，是否還會(huì)有“相交弦定理”呢？這樣的探究就會(huì)看到“云起時(shí)”．如圖2，把2條弦AE和AF移開，變成2條相交弦，切線變成割線，結(jié)論1的條件是橢圓中2條弦相交點(diǎn)在橢圓上，如果2條弦相交點(diǎn)不在橢圓上時(shí)，通過研究還可以得到一般性結(jié)論．

圖3

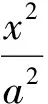
(a2+b2t2)y2+2tmb2y+b2m2-a2b2=0.

設(shè)C(x1,y1)，E(x2,y2),則

同理可設(shè)Q(x3,y3)，F(xiàn)(x4,y4)，則

從而

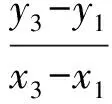
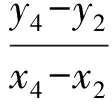
記kCD+kEF的分子為

μ= (y3-y1)[-t(y4+y2)+n-m]+

(y4-y2)[-t(y3+y1)+n-m]=-t(y3y4-

y1y2)+(n-m)[(y3+y4)-(y1+y2)]=

即kCD+kEF=0結(jié)論成立．

生5：由此,可以進(jìn)一步探究△PCD∽△PEF，得出結(jié)論：

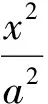
片段3會(huì)當(dāng)凌絕頂,一覽眾山小

師：是否可以把昨天作業(yè)中的數(shù)學(xué)問題由橢圓推廣到拋物線和雙曲線上？

(讓學(xué)生分小組討論、探究，再由代表進(jìn)行總結(jié)發(fā)言.)

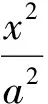
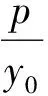
師：通過討論分析，還可以得到更一般的結(jié)論：

證明設(shè)圓錐曲線方程為

f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F=0,

(1)

直線PQR與直線PST的傾斜角分別為θ1,θ2，則過點(diǎn)P的直線PQR的參數(shù)方程為

(2)

聯(lián)立式(1)，(2)，得

PQ·PR=t1·t2=

同理可得

PS·PT=t3·t4=

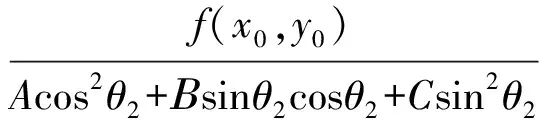
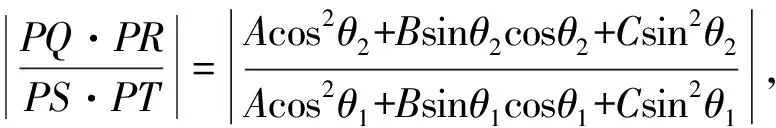
該值與點(diǎn)P位置無關(guān)．

特別地，當(dāng)B=0,θ1+θ2=π(即直線QR與直線ST的斜率互為相反數(shù))時(shí)，|PQ|·|PR|=|PS|·|PT|成立．

師：當(dāng)圓錐曲線換成圓時(shí)，就是圓冪定理．上述證明已涵蓋了圓冪定理，并且說明把圓推廣到橢圓、雙曲線、拋物線時(shí)，類似結(jié)論仍然成立．結(jié)論9是圓錐曲線的牛頓定理，它的特例包含了今天我們所探究的所有結(jié)論，此結(jié)論可以作為編寫相關(guān)圓錐曲線試題的依據(jù)或根源．

師(結(jié)束語)：同學(xué)們，優(yōu)美的結(jié)論、奇妙的數(shù)學(xué)，令人神往．在平常的學(xué)習(xí)中，要做學(xué)習(xí)的有心人，處處留心皆學(xué)問，讓我們探究數(shù)學(xué)、喜歡數(shù)學(xué)、享受數(shù)學(xué)吧!

2 課后思考

2.1 摒棄知識(shí)灌輸，營造探究環(huán)境

高三數(shù)學(xué)復(fù)習(xí)時(shí)間緊、任務(wù)重，教師往往把思維變成即成思路，精心備好課，準(zhǔn)備若干解題方法，整個(gè)課堂以講解為主，使問題解答變成可傳信物，學(xué)生看到的是思維的結(jié)果，很難體會(huì)思維的過程．事實(shí)上,很多學(xué)生并不一定會(huì)像教師那樣去思考、去探究，原因是：思維是靠啟迪，而不是靠灌輸，越是傳授得一清二楚，學(xué)習(xí)者就越不會(huì)思維．因此在教學(xué)時(shí)要給學(xué)生獨(dú)立思考、自由發(fā)現(xiàn)問題進(jìn)而解決問題的機(jī)會(huì)，有意培養(yǎng)其自主探究的能力和習(xí)慣，從而提高學(xué)生的后期繼續(xù)學(xué)習(xí)的能力．復(fù)習(xí)課營造良好的探究環(huán)境，是提高數(shù)學(xué)課堂教學(xué)效果的關(guān)鍵，是發(fā)展學(xué)生數(shù)學(xué)學(xué)習(xí)能力的根本．本節(jié)課教學(xué)設(shè)計(jì)的策略是啟發(fā)引導(dǎo)學(xué)生跨越探究的三重境界，從“不畏浮云遮望眼,只緣身在最高層”的堅(jiān)持到“行到水窮處，坐看云起時(shí)”的困惑再到“會(huì)當(dāng)凌絕頂,一覽眾山小”的頂峰境界，使學(xué)生充分品味探究過程的魅力，體驗(yàn)數(shù)學(xué)學(xué)習(xí)的樂趣．

2.2 運(yùn)用合作學(xué)習(xí)，促進(jìn)有效探究

小組合作學(xué)習(xí)是新課程理念下比較常用的一種教學(xué)手段，但并不是所有的內(nèi)容都適合合作學(xué)習(xí)，只有那些抽象的、深刻的、具有開放性的問題，才需要合作學(xué)習(xí)．本節(jié)課教學(xué)班級(jí)的學(xué)生屬中偏下水平，如果讓學(xué)生獨(dú)立去思考探究，能夠得到結(jié)論7和結(jié)論8的學(xué)生畢竟少數(shù)．事實(shí)證明，通過合作學(xué)習(xí)，學(xué)生的積極性得到很大的提高，課堂氣氛熱烈，結(jié)論7和結(jié)論8的合作發(fā)現(xiàn)也為師生共同探究，為得到結(jié)論9起到了很好的鋪墊作用．有效的合作學(xué)習(xí)，可以使數(shù)學(xué)課堂充滿活力，更能揭示數(shù)學(xué)本質(zhì)，可以使數(shù)學(xué)課堂充滿智慧，更有內(nèi)涵，探究更有成效．

2.3 把握探究方式，提高復(fù)習(xí)效率

數(shù)學(xué)探究式課堂教學(xué)，主要是指在數(shù)學(xué)課堂教學(xué)中，學(xué)生在教師的指導(dǎo)下，用類似科學(xué)研究的方式去解決問題的學(xué)習(xí)方式．“類似科學(xué)研究的方式”就是讓學(xué)生通過觀察、比較、類比、猜想等方式發(fā)現(xiàn)問題，提出結(jié)論，進(jìn)行推理和證明解決問題．其實(shí)質(zhì)是讓學(xué)生學(xué)習(xí)科學(xué)研究的思維方式，從而培養(yǎng)學(xué)生主動(dòng)探究、體驗(yàn)數(shù)學(xué)發(fā)現(xiàn)和創(chuàng)造的歷程，發(fā)展他們的創(chuàng)新意識(shí)．這節(jié)復(fù)習(xí)課從一道好題出發(fā)，從橢圓性質(zhì)到一般圓錐曲線性質(zhì)，從圓冪定理推測(cè)出圓錐曲線也有類似“圓冪定理”的結(jié)論，達(dá)到了“秀枝一株，嫁接成林”的目標(biāo)，教學(xué)設(shè)計(jì)高屋建瓴，潛移默化，淺入深出，最后走向“以不變應(yīng)萬變”的“一課一例”的復(fù)習(xí)課模式．

總之，本節(jié)課通過對(duì)橢圓性質(zhì)的探索，合理地運(yùn)用幾何直觀去推測(cè)，或是出于直覺，或是通過歸納和類比，體現(xiàn)了一種自然思考的過程．課堂上不但提出了幾個(gè)新的結(jié)論，而且在猜測(cè)和證明的過程中，體現(xiàn)了科學(xué)研究的一般規(guī)律，有利于激發(fā)學(xué)生的興趣．因此，在日常教學(xué)中，我們要注意挖掘探究素材，讓學(xué)生在“一題多解、一題多變、多題歸一”中體會(huì)題目的數(shù)學(xué)本質(zhì)，領(lǐng)悟解題的思想方法，促進(jìn)學(xué)生創(chuàng)新思維的發(fā)展．

[1] 李士锜.數(shù)學(xué)學(xué)習(xí)心理[M].上海：華東師范大學(xué)出版社，2001：64-65.

[2] 王順耿.再論圓錐曲線“相交弦定理”的探索[J].數(shù)學(xué)教學(xué)，2008(7):31-37.