區域金融發展和經濟增長的計量分析

王芳　劉偉宏

[摘要]金融發展與經濟增長關系的研究一直是經濟學界討論的熱點問題。該文基于福建省1980年～2011年的數據，運用分位數回歸方法，考察了金融發展和經濟增長之間的關系。與經典的條件均值回歸相比，條件分位數回歸方法能夠挖掘數據生成過程更加全面深入的信息，為研究區域金融發展與經濟增長的關系提供有力的證據。

[關鍵詞]福建省 金融發展 經濟增長 分位數回歸

1.概述

國內外經濟學家對金融發展與經濟增長之間的關系進行了頗具深度的探討，通過理論分析和實證研究得到了豐富的成果。近些年來，為了促進經濟快速健康發展，不少發展中國家把金融發展作為推動經濟增長的重要引擎。1973年，麥金農和肖分別提出“金融抑制”和“金融深化”。麥金農認為，發展中國家為了早日實現工業化的目標，企圖低成本地利用國內外金融資源，于是對內壓低存貸款利率，對外高估本國利率，從而導致金融市場喪失了調節資金供求關系的能力。因此，要實現金融發展，必須消除金融抑制。肖從金融深化的角度得出了類似的結論，他認為，金融深化能夠通過儲蓄效應、投資效應、收入效應、就業效應和分配效應促進一個國家的經濟發展。“金融抑制”和“金融深化”理論強調市場的形成和完善，并沒有強調金融結構問題，但對發展中國家來說，由于金融發展水平低，金融深化也隱含著金融結構的進步。

20世紀90年代以來，內生經濟增長理論的發展，指出金融中介和金融市場的內生性，以及金融發展和經濟增長之間的關系。King（1993）的實證研究結果表明，金融機構和經濟增長之間存在較強的相關關系，而且金融發展可以比經濟發展更快。Levine（1997）從功能的角度闡釋了經濟增長中金融發展的作用，金融中介為風險管理和流動性提供了機會，憑借著有吸引力的風險分擔特性，激發了金融市場和工具的發展。Greenwood（1997）通過建立金融市場的內生形成模型發現了金融發展和經濟增長之間的雙向因果關系，指出金融市場和金融中介的運行成本或參與成本導致了金融市場和金融中介的內生形成。Levine和Zervos（1998）把一些反映股票市場發展狀況的指標添加到回歸模型中從而擴展了King和Levine（1993）對金融中介和經濟增長關系的分析，根據47個國家1976年-1993年的數據進行實證后得出結論：股票市場流動性和銀行發展不僅都與同時期的經濟增長存在很強的正相關關系，而且能很好地預測經濟增長前景。

與國外浩如煙海的研究文獻相比，國內對中國金融發展與經濟增長關系問題的研究起步較晚。但是，隨著我國國民經濟的持續快速發展和金融體系改革的不斷深化，金融部門對經濟增長作用如何日益引起國內學者的廣泛關注。他們發表了大量理論分析和實證研究的文章，對中國未來金融和經濟政策的制定和完善進行了卓有成效的探索。

談儒勇（1999）利用季度數據對金融發展與經濟增長之間的關系進行了實證分析，對中國整體金融發展與經濟增長關系研究做出開創性貢獻。韓廷春（2002）把金融發展作為一個因素引入內生經濟增長模型，并利用中國的數據進行實證檢驗，其結論表明生產過程中的人力資本和R&D;水平越高，非國有經濟投資額占總投資額比例越大，則投資效率越高，從而促進經濟增長越快。王景武（2005）利用誤差修正模型和格蘭杰因果檢驗對我國區域金融發展與經濟增長關系進行了計量分析，得到的結論是東部地區的金融發展與經濟增長之間存在正向因果關系，而西部地區金融發展與經濟增長之間關系則存在相互抑制關系。

事實上，由于中國經濟發展的非均衡性，區域金融發展和經濟增長之間關系的分析，具有更加現實的意義。本文以基于福建省的年度統計數據，運用條件分位數回歸方法進行區域金融發展與經濟增長關系的計量分析，采用的計量經濟學軟件是Eviews。

2.福建省金融發展與經濟增長：條件分位數回歸

線性分位數回歸理論由Koenker和Bassett（1978）最早提出，是估計一組回歸變鰱與被解釋變量的分位數之間線性關系的建模方法。分位數回歸通過對古典條件均值模型為基礎的最小二乘法進行延伸，用多個分位函數來估計整體模型。相比普通最小二乘回歸只能描述自變量對于因變量局部變化的影響而言，分位數回歸能更精確地描述自變量對于因變量的變化范圍以及條件分布形狀的影響，不僅分析被解釋變量的條件期望（均值），還能夠分析解釋變量對被解釋變量的中位數、分位數等的影響。不同分位數下的回歸系數估計量常常不同，即解釋變量對不同水平被解釋變量的影響不同。而且，分位數回歸對誤差項并不要求很強的假設條件，因此對于非正態分布而言，分位數回歸系數估計量則更加穩健。

在經濟增長的實證研究文獻中，人們常常運用生產函數作為基本估計框架。這里也將它用于分析區域金融發展與區域經濟增長關系的實證研究，假定總量生產函數（t期）的形式，把總產出抽象為金融發展水平與控制變量的函數，控制變量是除金融發展水平以外的其它主要影響因素，可以用函數表示：

Yt=f（fiancet，controlt）

其中，Yt是總產出，一般用GDP表示，financet代表金融發展水平，controlt代表控制變量。為了根據可得數據研究福建省的金融發展與經濟增長之間的關系，這里被解釋變量取國內生產總值反映經濟增長，用GDP表示；解釋變量是金融發展水平和控制變量。金融發展水平采用金融相關比率指標，即FIR，等于金融機構存貸款總額與GDP的比值。控制變量是指那些能夠影響經濟增長的資源稟賦差異的變量，目的是用來控制其它可能導致經濟增長差異的因素。（1）實物資本投入，用固定資產投資占GDP的比值反映物質資本的投入水平，用INFIXP表示。（2）人力資本投入，一般用中小學畢業升學率或者政府財政支出中的教育支出近似反映各地區人力資本水平。考慮到財政金融的緊密聯系，這里設置了政府財政支出總額占GDP的比值綜合近似反映人力資本水平，以及財政金融的緊密聯系，用LGEXPP表示。（3）經濟開放程度，考慮到外國直接投資額與金融的緊密聯系，這里設置了外國直接投資額（或者實際利用外資）總額占GDP的比值綜合近似反映經濟開放程度，以及外國直接投資與金融的緊密聯系，用FDIAUP表示。

根據以上的分析，為了進行彈性研究，對被解釋變量和解釋變量都取自然對數，則計量分析模型的基本形式為：LnGDP=po+pILnFIR+p2LnINFIXP+D3Ln LGEXPP+

B4Ln FDIAUP+μ

為了對比研究結果，以下將采用條件均值回歸和條件中位數回歸進行計量分析，它們的結果分別見表1和表2。

由于條件均值回歸和條件中位數回歸采用的計算方法不同，得到的擬合優度值存在明顯差異。一般來說，如果采用相同的數據，偽擬合優度值（Pseudo R-squared）明顯小于擬合優度值（R-squared），調整的偽擬合優度值（Adjusted PseudoR-squared）明顯小于調整的擬合優度值（Adjusted R-squared）。從表1和表2可以看出，偽擬合優度值是0.841360，擬合優度值是0.960442；調整的偽擬合優度值是0.817858；調整的擬合優度值是0.954582。

另外，比較兩種方法估計得到的解釋變量的系數，存在明顯的小同。三個解釋變量（INFIXP、LGEXPP、FDIAUP）系數的條件均值回歸估計值的絕對值大于條件中位數回歸估計值的絕對值，一個解釋變量（FIR）系數的條件均值回歸估計值的絕對值小于條件中位數回歸估計值的絕對值。四個解釋變量系數對應的條件均值回歸估計值與條件中位數回歸估計值的符號相同。

為了深入探究金融發展和其它控制變量對經濟增長的影響在經濟增長不同水平下的差異，接下來對經濟增長的多個分位數水平進行條件分位數回歸估計。

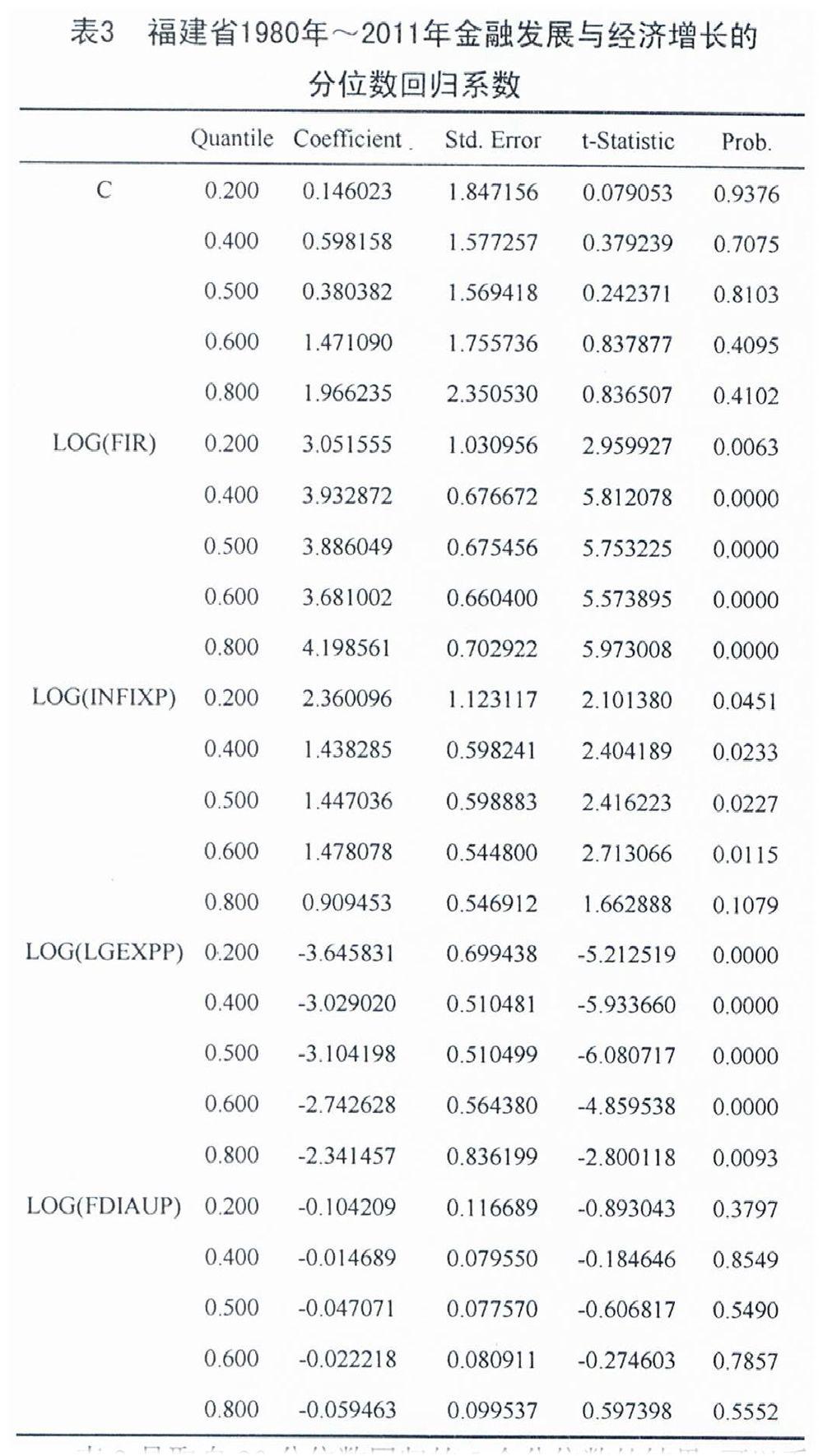
表3是取自20分位數回歸的5個分位數的結果，可以看出，在經濟增長的不同分位數水平上，金融發展和其他控制變量對經濟增K的作用大小存在差異。在解釋變量LnGDP不同的分位數水平，解釋變量LnFIR和Ln INFIXP的系數都是正數，而解釋變量Ln LGEXPP和Ln FDIAUP的系數都是負數。從絕對值方面比較，解釋變量LnFIR和LnLGEXPP的系數較大，LnlNFIXP的系數次之，LnFDIAUP的系數最小。

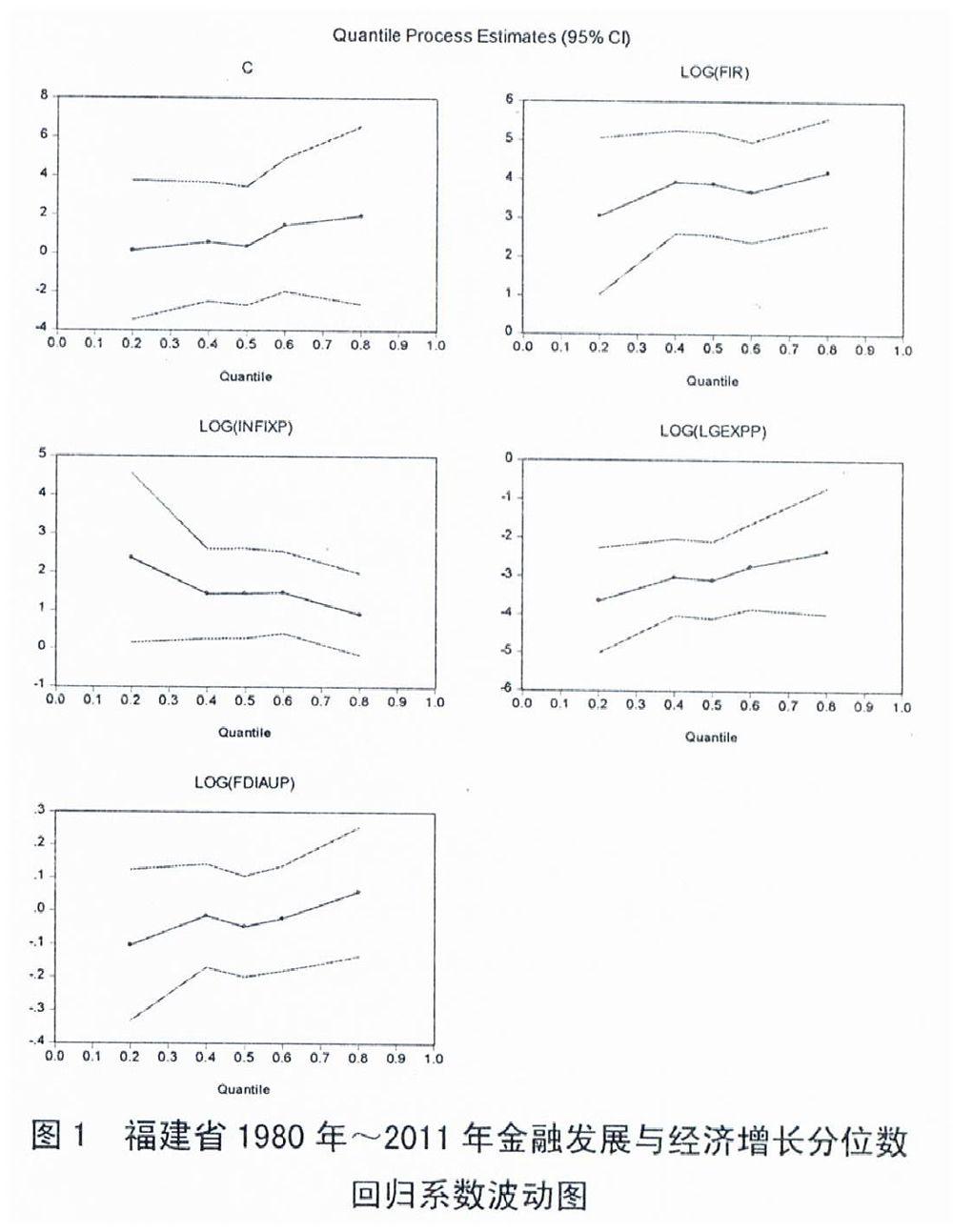
從圖1可以看出，隨著經濟增長分位數水平的變化，每個解釋變量對經濟增長的影響大小隨之改變。當被解釋變量LnGDP的分位數水平從0.2逐步增加到0.8，解釋變量系數的點估計（中間有圓點的折線）和區間估計（上下沒有圓點的折線）也隨之變化。從系數點估計的變化特點來看，截距項在0附近波動。解釋變量LnFIR的系數沒有明顯的變化趨勢，主要在3.5附近波動；解釋變量Ln INFIXP的系數在兩端有比較明顯的下降趨勢，中間從LnGDP的0.4到0.6分位數基本保持穩定；解釋變量Ln LGEXPP和LnFDIAUP的系數在兩端有比較明顯的上升趨勢，中間從LnGDP的0.4到0.6分位數基本保持穩定。

3.結論與建議

本文以福建省1980年至2011年的年度統計數據為基礎，實證分析了金融發展對區域經濟增長的影響。基于前面的分析，本文得出以下結論：條件中位數回歸和條件均值回歸的估計結果并不相同；與條件均值回歸相比較，條件分位數回歸對數據信息的分析更加全面深入。研究結果表明，在經濟增長的某個具體分位數水平，金融發展和其它控制變量對經濟增長影響的大小存在差異，表現了解釋變量作用的不同；在經濟增長的不同分位數水平，某個具體的解釋變量（金融發展和其它控制變量）對經濟增長影響的大小也不一樣，說明解釋變量的作用并不穩定。這些基本結論能夠幫助我們在制定協同區域經濟增長和金融發展的政策時提供重要的理論指導。