導軌滑塊結合部的非線性剛度等效建模研究*

楊 濤 張為民② 楊 勇

(①同濟大學機械與能源工程學院，上海 201804;②同濟大學中德學院，上海 200092)

作為精密的直線導向運動部件和機床中的重要結合部，直線滾動導軌的剛度特性直接影響機床的加工精度和使用性能。研究直線滾動導軌結合部的剛度性能，對預測和評估機床的性能具有重要意義。圍繞直線滾動導軌的剛度特性，國內外學者已做了大量研究工作，常用的研究方法包括:理論分析法［1－2］、有限元法［3－4］、試驗測試法［5－6］，取得了很多研究成果，但仍存在以下問題:(1)在研究導軌滑塊結合部剛度特性時，往往忽略因結合部預緊造成的剛度非線性現(xiàn)象;(2)為保證結合部建模的準確性常需要對滾珠進行建模，從而造成運算時間與成本較高;(3)結合部剛度試驗測試法雖精度較高，但缺乏通用性，無法在產(chǎn)品的設計階段進行有效的性能預測與評估。

綜上所述，本文以導軌滑塊結合部為研究對象，基于彈性力學及其赫茲接觸理論，在分析計算預緊情況下導軌滑塊結合部力－位移剛度曲線的基礎上，以非線性彈簧進行等效，并采用含滾珠的結合部有限元模型與非線性等效彈簧有限元模型進行仿真計算，在首先保證其剛度特性的前提下，降低運算成本，簡化計算過程，并且對結合面應力分布影響盡可能小。

1 導軌滑塊結合部的剛度特性

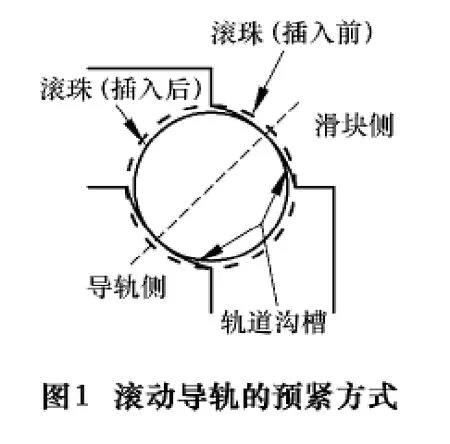
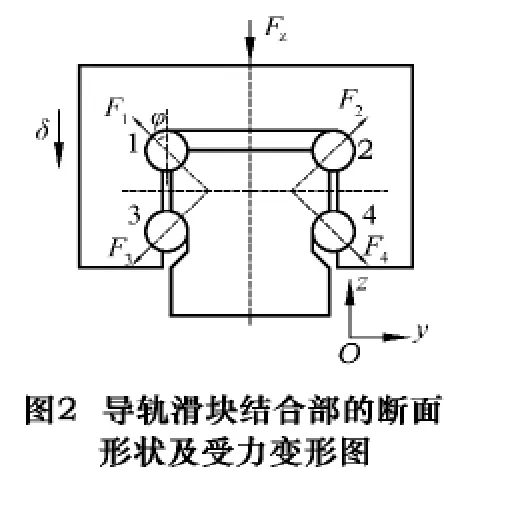
目前滾動導軌的主要預緊方式如圖1所示，即采用滾珠直徑大于溝槽尺寸的方式進行預緊，從而達到增加剛度的目的。本文采用該方式進行預緊。通常情況下導軌滑塊承受的主要工作負載為垂向載荷，通過計算滑塊位移δ隨垂向載荷Fz的變化情況，能夠比較準確地得到導軌滑塊結合部的剛度特性。圖2為導軌滑塊結合部的斷面形狀及受力變形圖，1、2、3、4表示滾珠號碼，F(xiàn)1、F2、F3和F4表示滾珠所受的接觸力。

1.1 理論分析

在進行剛度計算時，根據(jù)赫茲彈性接觸理論及直線滾動導軌結合部的特點，作如下假設［1］:①除接觸部分以外，均作為剛體考慮;②導軌和滑塊的滾動溝槽幾何形狀完全相同;③斷面的幾何形狀左右對稱;④只承受垂直方向的載荷;⑤滾珠過盈裝配到溝槽時，接觸角不發(fā)生改變;⑥滾珠以兩點接觸滾動。

本文定義導軌溝槽與滾珠曲率比fr=Rr/Da，滑塊溝槽與鋼球曲率比fs=Rs/Da，由假定條件②可知fr=fs=f，曲率和B=fr+fs－1=2f－1。其中，Rr為導軌溝槽半徑，Rs為滑塊溝槽半徑，Da為插入溝槽后滾珠的直徑。

1.1.1 幾何關系

(1)上排滾珠

如圖3所示，滑塊受到垂直載荷作用，設滑塊和導軌溝槽半徑的中心由A垂直位移到A′，則A′A′=Rr+Rs－Da+ δnr1+ δns1。其中，δnr1、δns1分別為導軌接觸部分和滑塊接觸部分的法向彈性變形。定義 δn1=δnr1+δns1，則

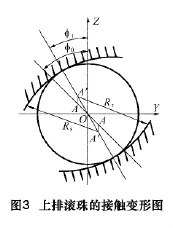
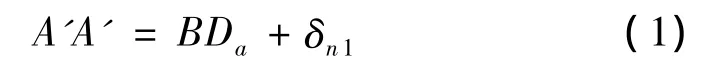
因幾何約束的關系，在承受垂直載荷時，滑塊在Y方向不產(chǎn)生位移變化，故A′A′sinφ1=AAsinφ0，即

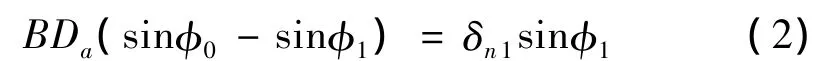
設滑塊和導軌之間在Y方向的趨近量為δ，則

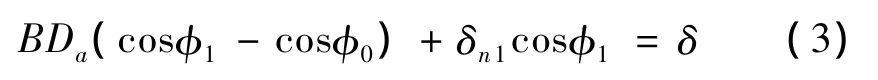
由式(2)和(3)可求得

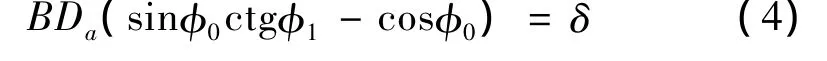
(2)下排滾珠

如圖4所示，當滑塊受到垂直載荷作用時，下排滾珠的預壓載荷逐漸釋放。設滑塊和導軌溝槽半徑的中心由B垂直位移到B′，則B′B′=Rr+Rs－Da－ δnr2－ δns2。式中:δnr2、δns2分別為導軌接觸部分和滑塊接觸部分的法向彈性變形恢復量。定義δn2= δnr2+ δns2，則

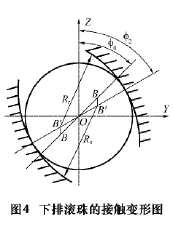
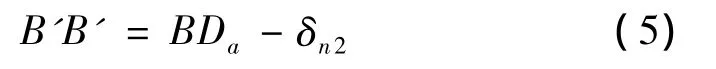
同理，在Y方向有B′B′sinφ2=BBsinφ0，即

根據(jù)1.1中假定條件①可知，與下排滾珠接觸的滑塊和導軌之間在Z方向的趨近量仍為δ，則

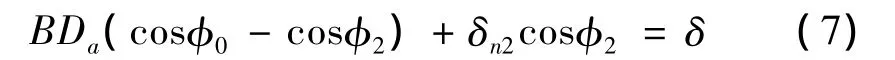
由式(6)和(7)可求得

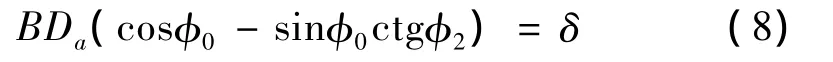
1.1.2 物理關系

(1)彈性變形系數(shù)kn的求解［7］

根據(jù)赫茲接觸理論，滾珠與導軌、滑塊接觸面彈性力與彈性變形的關系為

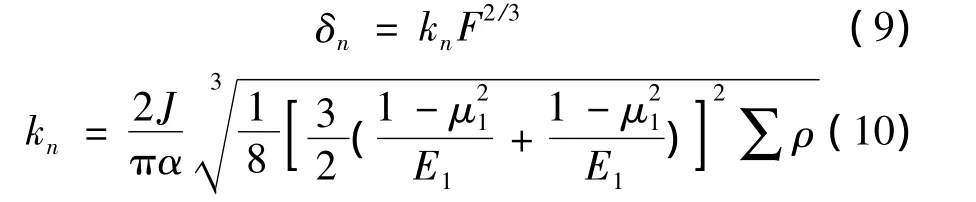
式中:δn為接觸區(qū)法向彈性變形;kn為彈性變形系數(shù);F為作用于兩彈性體接觸點的法向壓力;J、α為由接觸點主曲率τ值決定的系數(shù);E1、E2為兩接觸體材料的彈性模量;μ1、μ2為兩接觸體材料的泊松比;∑ρ為兩接觸體接觸點處4個主曲率之和。

(2)上、下兩排滾珠同時受壓時的受力分析

如圖2所示，當垂向載荷Fz作用在滑塊上時，各列中單個滾珠的彈性力分別為F1、F2、F3和F4，由于導軌滑塊結合部在Y方向上受力平衡，且由于Y方向的對稱性，則有

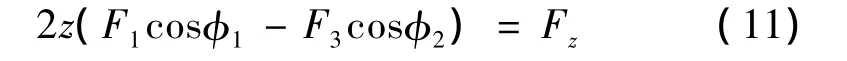
式中:z為接觸鋼球數(shù)。接觸點的法向彈性變形由赫茲理論可求得

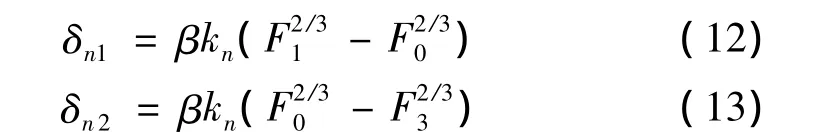
式中:β為引入的修正系數(shù);F0為單個滾珠的預緊力，且F0=P/(2zcosφ0)。將式(2)與(6)分別代入式(12)和(13)可求得

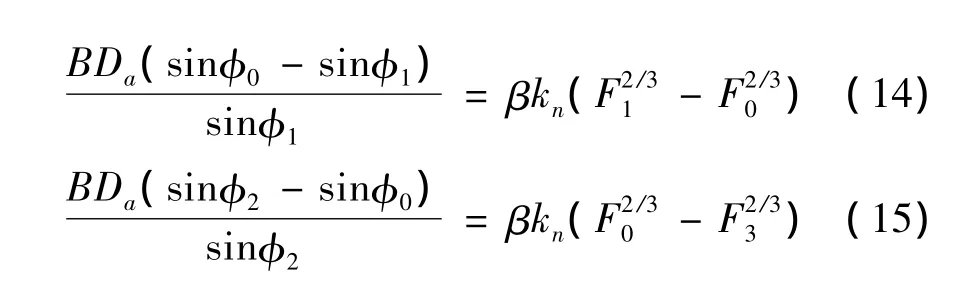
(3)下排滾珠恢復預變形后的受力分析

當δ達到某一定值，下排滾珠將不再受壓，即F3=F4=0，式(11)可轉化為

1.1.3 算例

本文以一款直線滾動導軌為例，將本文所建立的導軌滑塊結合部模型，應用于直線滾動導軌的垂向剛度特性分析，驗證理論模型的有效性。該型號直線滾動導軌的相關參數(shù)為:滾珠直徑Da=6.35 mm;曲率比f=0.54;接觸滾珠數(shù)z=15;預壓載荷P=2 940 N;初始接觸角φ0=45°;材料彈性模量E=208 000 MPa;泊松比μ=0.3。

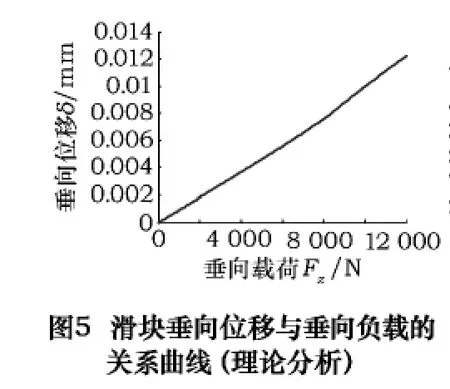
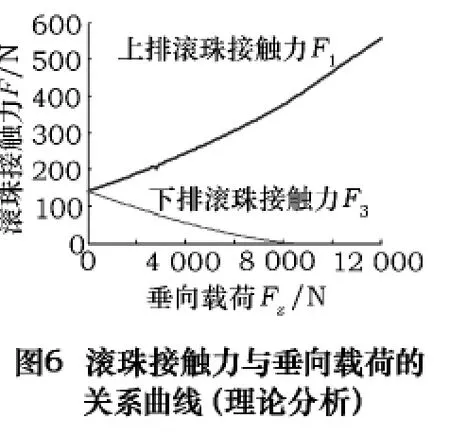
根據(jù)式(4)、(8)、(11)、(14)、(15)進行計算，可以得到考慮預壓載荷情況下導軌滑塊的剛度特性。圖5所示為滑塊垂向位移與其承受垂向載荷的關系曲線。圖6所示為結合部中滾珠所受法向接觸力與滑塊承受垂向載荷的關系曲線。從圖中可以看出，當垂向載荷Fz在8 400 N附近時，下排滾珠接觸力F3減小到0，此時結合部剛度發(fā)生突變，剛度特性曲線將出現(xiàn)拐點。

1.2 導軌滑塊結合部有限元建模

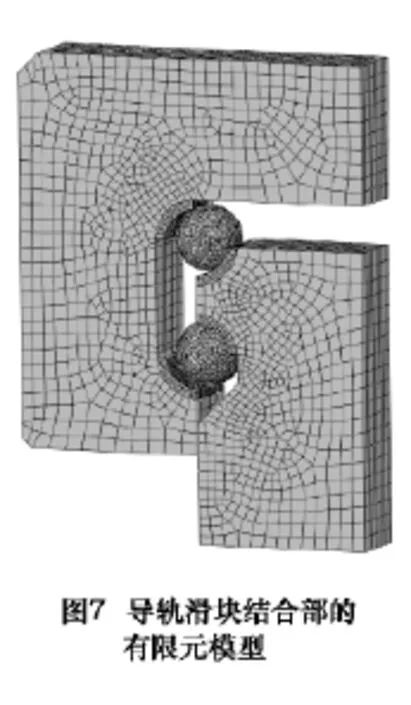
考慮結合部結構的對稱性，本文取導軌滑塊結合部的左半切片建立有限元模型，并施加對稱約束，如圖7所示。

2 等效彈簧簡化模型的剛度特性

滾珠在整個承載過程中，都是通過自身的彈性變形對導軌滑塊接觸面提供反向接觸力，且接觸力與彈性變形量存在一一對應關系，變形量越大，接觸力越大，與彈簧的性質相似。鑒于此，考慮把結合部中的滾珠簡化為等效彈簧。通過修正彈簧非線性剛度使簡化前后的剛度特性保持一致。

2.1 理論分析

2.1.1 幾何關系

將帶有預緊載荷的滾珠等效為帶預壓變形的彈簧單元，彈簧的初始長度為Da，認為彈簧與導軌連接的M、P點固定不動。

(1)上排等效彈簧

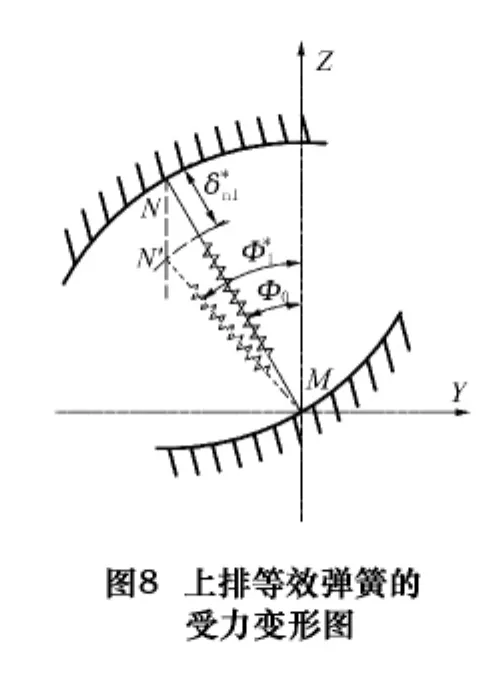
如圖8所示，結合部承受垂向載荷后，彈簧與滑塊的接觸點從N垂直移動至N′，產(chǎn)生位移為δ，則

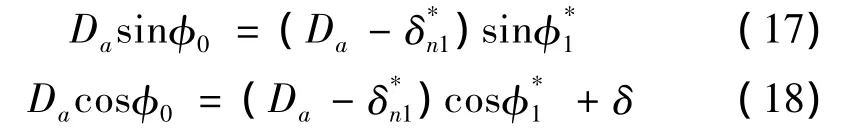
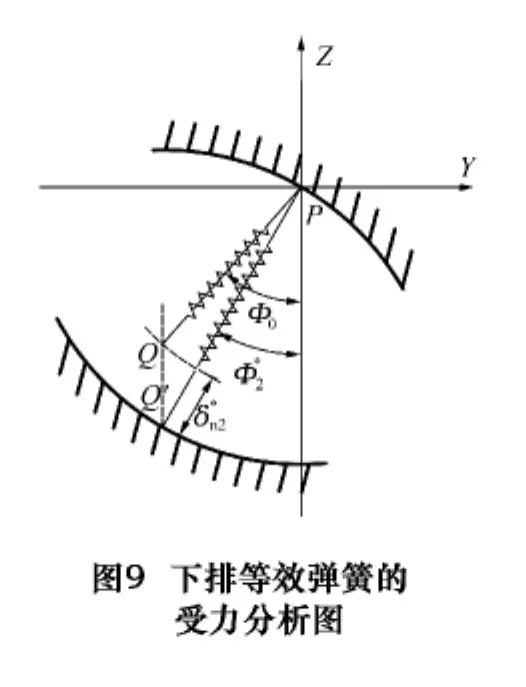
(2)下排等效彈簧

如圖9所示，結合部承受垂向載荷后，彈簧與滑塊的接觸點從Q垂直移動至Q′，由于滑塊與滾珠的非接觸部分都作為剛體處理，則與下排滾珠接觸的滑塊和導軌之間在Z方向的趨近量仍為δ，則有

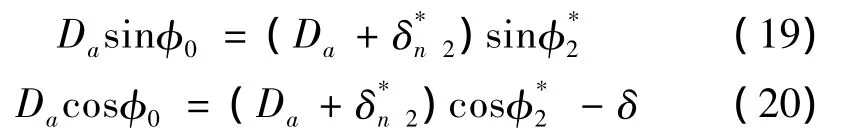
2.1.2 物理關系

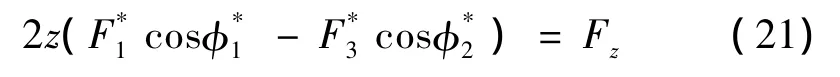
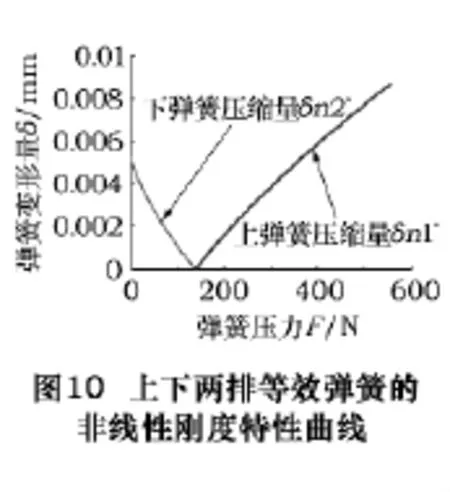
為了將簡化后的等效彈簧結合部模型與原結合部模型的剛度特性保持一致，現(xiàn)將圖5所示的結合部剛度特性函數(shù)代入式(17～21)中，通過計算可以得到上下兩排等效彈簧的彈簧壓力與彈簧變形量的關系曲線如圖10所示。

2.2 導軌滑塊簡化模型的有限元建模

使用彈簧單元替換原結合部有限元模型中的滾珠，如圖11所示。將彈簧的兩個端點分別與所接觸溝槽的區(qū)域進行耦合，耦合面積通過赫茲理論計算得到。設置彈簧單元的非線性剛度如圖10所示，并進行分析計算。

3 結果與分析

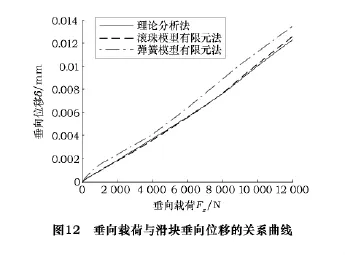
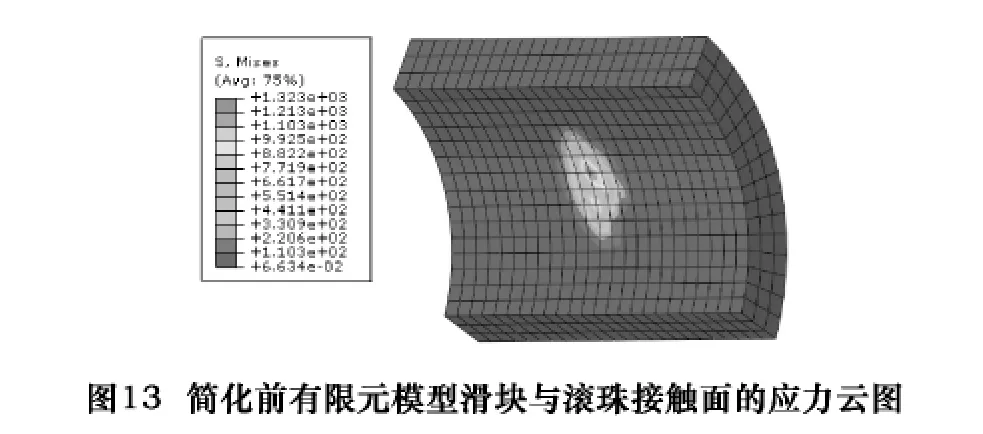
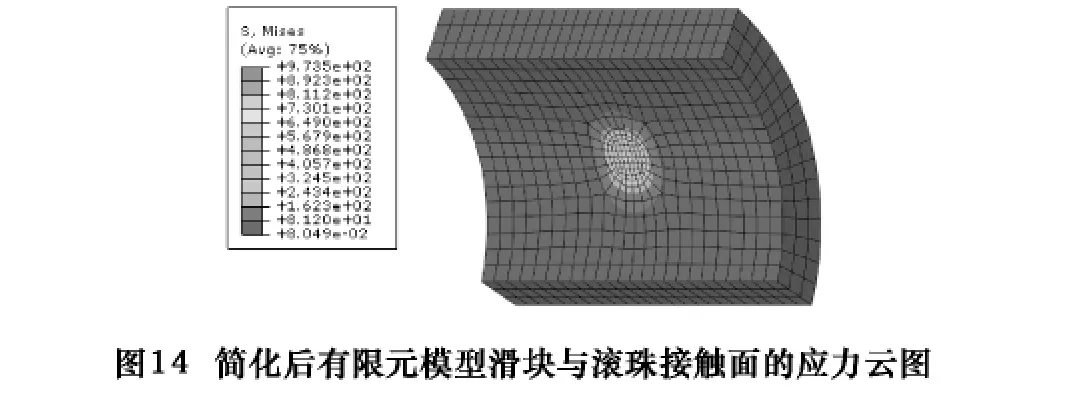
簡化前后有限元模型結合部的剛度特性曲線與理論分析結果進行比較，如圖12所示。可以看出，簡化前后結合部的垂向剛度非常接近，并且與理論計算得到的垂向剛度曲線非常吻合。簡化前后兩種結合部模型中滑塊與滾珠接觸面的應力云圖如圖13、14所示，可以看出，其應力分布情況大致吻合，綜上可以看出該簡化方法的合理性。

4 結語

(1)采用含滾珠的非簡化有限元模型分析得到的剛度特性曲線與基于彈性力學和赫茲理論計算所得結果非常吻合，并且均存在明顯的曲線拐點，驗證了該滾珠結合部有限元模型的準確性與可靠性。

(2)采用非線性等效彈簧有限元模型，在大大降低計算成本和計算時間的基礎上，得到的剛度特性曲線與含滾珠結合部模型計算結果的最大誤差約為8%，而應力云圖分布也大致吻合，從而說明了非線性等效彈簧簡化模型的可行性與有效性。

(3)該研究為在產(chǎn)品設計階段研究導軌滑塊結合部的剛度特性、預測與評估產(chǎn)品性能提供了重要的方法和理論依據(jù)。

［1］孫健利.直線滾動導軌機構承受垂直載荷時的剛度計算［J］.華中理工大學學報，1988，16(5):35 －39.

［2］孫健利.精密直線滾動導軌的預加載荷及剛度計算［J］.華中理工大學學報，1988，16(6):125 －130.

［3］Dadalau A，Groh K，Reu M，et al.Modeling linear guide systems with CoFEM:equivalent models for rolling contact［J］.Production Engineering，2012，6(1):39 －46.

［4］李小彭，聶巍，趙志杰，等.直線導軌副動態(tài)特性的實驗研究及有限元分析［J］.組合機床與自動化加工技術，2011(10):17－20.

［5］劉建素，李準.滾動直線導軌副靜剛度試驗［J］.制造技術與機床，1997(7):12－13.

［6］張耀滿，劉春時，謝志坤，等.數(shù)控機床直線滾動導軌結合面有限元分析［J］.制造技術與機床，2007(7):75－78.

［7］蔣書運，祝書龍.帶滾珠絲杠副的直線導軌結合部動態(tài)剛度特性［J］.機械工程學報，2010，46(1):92 －99.

［8］程光仁，施祖康，張超鵬.滾珠螺旋傳動設計基礎［M］.北京:機械工業(yè)出版社，1987.

［9］毛寬民，李斌，謝波，等.滾動直線導軌副可動結合部動力學建模［J］.華中科技大學學報，2008，36(8):85 －88.