基于提升小波與RLS的渦輪泵故障檢測方法

鐘福利，李 輝

(電子科技大學航空航天學院，成都611731)

1 引言

隨著航天技術的快速發展，運載火箭的可靠性和安全性受到廣泛的重視，其故障檢測和診斷技術研究是一項十分重要的研究課題，得到許多研究人員和學者的關注［1-2］。渦輪泵是液體火箭發動機重要的機械部件之一，其結構十分復雜，物理環境極端，在發動機的部件中所占故障比率最高［3］。渦輪泵的故障擴展十分迅速，故障危害極大，故開展渦輪泵故障檢測，對減少由于渦輪泵故障造成的損失具有重要意義。近年來，國內外對運載火箭發動機及其渦輪泵等的健康監控研究也取得了一系列成果［2，4-5］，其中健康監測方法大部分以振動信號的時域特征、頻域特征、時頻域特征分析為基礎［6］。

基于時域信號統計特征的渦輪泵故障檢測算法較為普遍，有ATA算法、多特征參量自適應閾值綜合決策算法、渦輪泵實時故障檢測短數據均值自適應閾值算法［7-9］等。此類算法計算直接、簡便，計算量較小，運算速度快，實時性較好，但時域統計特征受隨機因素影響較大，使檢測中出現虛警和漏警的概率相對較大。基于頻域特征的故障檢測算法［10-11］，涉及的變換復雜，計算量較大，檢測的速度較慢，而且此類算法以信號平穩為前提，這對非平穩信號則會失效。基于時頻域的故障檢測算法，較典型的有以小波變換為基礎的檢測算法［12］，具有較好的分析非平穩信號和信號局部特性檢測能力，但也存在運算量相對較大的問題。

在機械故障檢測中，由于經典小波變換同時具有時域和頻域局部化特性，且有快速算法，故其得到了廣泛的應用。隨著小波提升方案的提出，小波分析的研究領域得到大大拓展。提升小波方案直接在時域或空域構造小波，具有算法簡單、計算速度快的特點［13］。遞推最小二乘算法(RLS)中濾波器的參數可用迭代的方式自適應更新，收斂速度快，并且具有較好的跟蹤系統和環境的動態變化的能力［14］。

因此，本文結合提升小波變換和RLS算法的優點，針對渦輪泵的穩態運行過程，提出一種基于提升小波與RLS的渦輪泵故障檢測方法，為渦輪泵的健康監控提供一種故障檢測方法。利用提升小波變換獲取每個檢測步長信號段的逼近信號和細節信號，計算每步各層細節信號和逼近信號的均方根以及峭度，計算逼近信號和細節信號的加權平均均方根、逼近信號的加權平均峭度和細節信號的加權平均峭度作為故障特征，分別提取逼近信號與細節信號的加權平均均方根和加權平均峭度作為故障特征，用RLS算法進行加權平均均方根特征序列濾波處理，根據給出的故障判別計算方法和故障判別方法分析渦輪泵的故障情況，并用某型發動機渦輪泵殼體振動加速度信號對方法進行了驗證。

2 檢測原理

2.1 提升小波變換

小波提升形式給出小波完全的空間域解釋，具有結構簡單，原位運算，節省存儲空間，運算量低，逆變換可直接反轉實現，有可逆的整數到整數的變換等優點。根據文獻［13］［15］和［16］對提升小波原理作如下簡介。

將給定的信號分解成逼近信號和細節信號，提升小波的提升方案實現包括分裂、預測和更新3個步驟:

1)分裂 將輸入信號Si分成Si-1和Di-1兩個小波子集，分解過程用FdivSi=(Si-1，Di-1)表示。將輸入信號按序號的奇偶分成兩組Ei-1(偶數號序列S2j)和Oi-1(奇數號序列S2j+1)。

2)預測 用偶數號序列Ei-1的預測值Pred(Ei-1)預測奇數號序列Oi-1，將預測算子Pred對偶數號序列作用后所得的值作為奇數號序列的預測值，奇數號序列的實際值與預測值相減得到殘差信號。用Pred(Ei-1)與Oi-1的差代替原來的Di-1，所得的Di-1表示信號的細節信息。

3)更新Si-1是經分解后得到的逼近信號，為了在逼近信號中保持原始信號的某些全局特性，其中最重要的是使其均值等于原信號Si的均值，不隨i的變化而改變，需對其更新。構造一個算子Upd，用信號細節Di-1子集來更新Si-1，采用公式(2)。

若對分解得到的逼近信號Si-1再進行以上步驟的分解即可得到原始信號的一個多級分解。

重構過程包括反更新、反預測和合并三個步驟。

1)反更新 給定Si-1和Di-1，由公式(3)計算恢復偶數號序列。

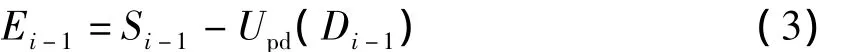
2)反預測 用反更新得到的Ei-1和給定的Di-1用公式(4)計算得到奇數號序列。

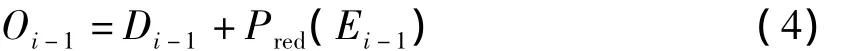
3)合并將恢復得到的奇數號序列和偶數號序列合并得到原始信號。合并表達式如(5)式所示。

式中Merge表示合并算子。

2.2 RLS 算法

RLS算法，用于設計自適應的橫向濾波器，遞推更新濾波器抽頭權系數。以下根據文獻［14，17］RLS算法作簡要的介紹。

假設j時刻輸入x(j)，期望信號為d(j)，則作為代價函數的指數加權的誤差平方和如(6)式所示:

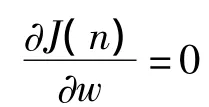
根據矩陣的求逆引理，可得R-1(n)的遞推公式

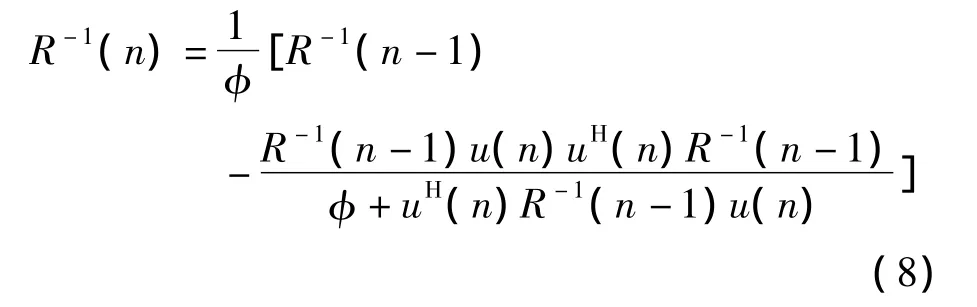
定義增益向量為

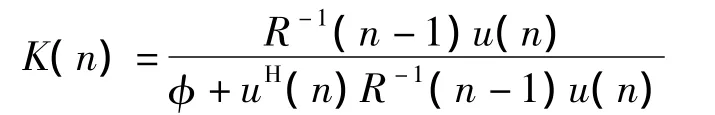
根據互相關矩陣r(n)、R-1(n)和w(n)可以求得

令P(n)=R-1(n)，RLS直接算法的基本步驟如下:

A.初始化w(0)=0，P(0)=σ-1I，其中σ是一個極小的數值;

B.更新計算濾波器系數按照下列式子迭代計算:

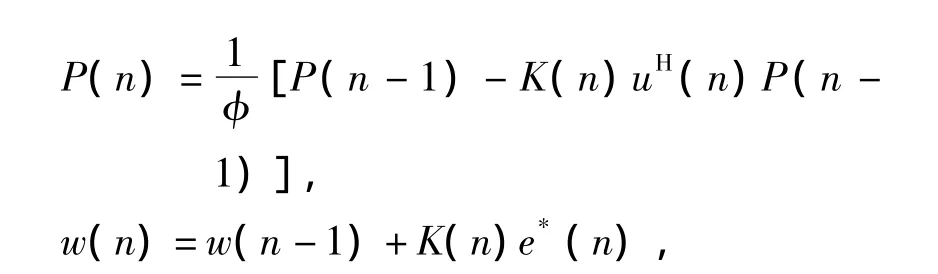
由此迭代更新濾波器系數。

2.3 基于提升小波與RLS的渦輪泵故障檢測

渦輪泵由于工作在高壓、高負載荷、溫度條件極端等惡劣環境中，承受來自自身振動和發動機其它振源的強烈振動的影響，故障發生概率較高且危害極大［2］。通過分析渦輪泵的緩變參數(如溫度、壓強等)和速變參數(振動位移信號、振動加速度信號等)可以監控其故障情況。振動信號富含渦輪泵工作狀態的信息，且對渦輪泵的狀態信息反映十分迅速、敏感，因此本文選擇渦輪泵的殼體振動加速度信號進行檢測分析。

渦輪泵的振動信號通常表現出非嚴格平穩特性，尤其在故障發生后非平穩性更突出。小波是分析非平穩信號的良好工具，它在機械故障檢測與診斷中取得較好效果［18-20］。提升小波繼承第一代小波的優點，而且其直接在時域或空域構造小波，具有計算速度快、易于硬件實現等特點。因此本文以提升小波變換為基礎提取故障特征。

由于發動機渦輪泵工作條件復雜，其振動信號受隨機因素的影響嚴重，呈現非線性、非平穩性，有必要對提升小波變換提取的故障特征序列進一步處理。鑒于RLS的優點，采用RLS算法對故障特征序列進行濾波和分析。

2.3.1 故障特征提取與計算

設S是待檢測信號，信號長度為L，按步長l將S劃分成M個信號段Sk，k=1，2，…，M，記信號段Sk為Sk(n)，n=1，2，…，l。將Sk(n)經提升小波分解和單支重構后得K層逼近信號和K層細節信號，分別記為Akj(n)，j=1，2，…，K，n=1，2，…，l和Dkj(n)，j=1，2，…，K，n=1，2，…，l，簡記為Akj和Dkj。峭度是無量綱參數，對沖擊信號特別敏感，加權平均均方根可以有效反映信號能量變化，故以此為基礎計算故障特征。

1)基于逼近信號的故障特征加權平均峭度用公式(11)和(12)來計算。

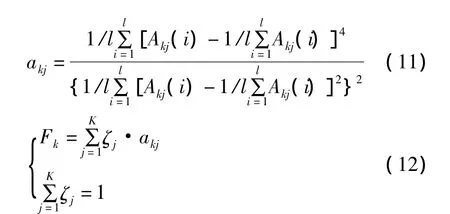
其中峭度影響系數 ζj∈［0，1］，表示各層信號的峭度序列對逼近信號整體峭度序列的影響系數，可根據各層信號對工作狀態的反映能力調整ζj大小，akj表示第k步的第j層逼近信號的峭度，Fk表示逼近信號的第k步的加權平均峭度。得到逼近信號的故障特征序列為(F1，F2，…，Fk，…，FM)。

2)基于細節信號的故障特征用公式(13)和(14)來計算。

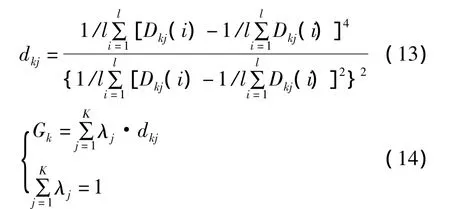
其中峭度影響系數λj∈［0，1］，λj表示第j層細節信號對細節信號整體的影響系數，dkj表示第k步第j層細節信號的峭度，Gk表示細節信號的第k步的加權平均峭度。獲得細節信號的故障特征序列為(G1，G2，…，Gk，…GM)。

3)基于低頻逼近信號與細節信號的故障特征用(15)、(16)和(17)計算。

其中 ψj∈［0，1］，均方根加權系數 ψj反映第j層信號對整體的影響程度的比例，Vkj(j＞0)和Vk0分別表示第k步第j層細節信號和第K層逼近信號的均方根，Wk表示細節信號與第K層逼近信號的第k步的加權平均均方根。得到細節信號與第K層逼近信號的故障特征序列為(W1，W2，…Wk，…WM)。提取了基于逼近信號和細節信號的故障特征后，即可將其用于RLS算法濾波和進行故障檢測。

2.3.2 故障判別決策

將提取的基于逼近信號與細節信號的加權平均均方根序列作為RLS算法的分析對象，采用RLS直接算法濾波。設輸出的故障特征(經RLS處理后的加權平均均方根和加權平均峭度)當前時刻值為Y(n)，前N個時刻的實際故障特征值為X(n)，…，X(n-N+1)。故障判別計算如式(18)和(19)所示:

其中τ是濾波輸出的當前特征點與其鄰近特征值的加權平均的比值閾值，其滿足 τ∈(1，+∞)，B(n)表示故障報警標號(B(n)為1時表示正常，為-1時表示異常)，加權系數κi表示鄰近特征點影響均值的程度。

在判定某一特征序列故障時，若連續n步內有(n-1)步檢出異常，則判定該故障特征序列檢出故障。本文采用3個故障特征序列，若有兩個或兩個以上的特征序列報故障，則判定系統故障。

2.3.3 故障檢測流程

基于提升小波與RLS的渦輪泵故障檢測方法的實現主要有以下幾個步驟:

第一步，初始化相應的參數，將原始信號按照設定的檢測步長進行分段，將每步信號用提升小波變換進行分解和單支重構，利用公式(11)～(17)計算基于逼近信號和細節信號的故障特征(逼近信號與細節信號加權平均均方根、逼近信號的加權平均峭度和細節信號的加權平均峭度)。

第二步，利用RLS直接算法對加權平均均方根序列濾波。

第三步，利用故障判別計算公式(18)和(19)計算判定故障特征序列是否異常，采用給出的故障判別決策綜合判定系統故障情況，以檢測渦輪泵的故障。

3 實驗驗證

為驗證故障檢測方法，本文選擇某型渦輪泵殼體的7段振動加速度信號(正常信號段NT1、NTr1、NTr2、NTr3 和故障信號段 FT1、FTr1、FTr2)作為試驗對象，7段信號均為模擬信號。將信號段NT1和FT1作為故障特征提取的分析信號;另外的6段信號被用于模擬渦輪泵穩態工作過程的故障檢測。

3.1 故障特征的分析驗證

為了分析故障特征對渦輪泵故障的敏感性和穩定性，試驗中選取正常的信號段NT1和故障信號段FT1，其中NT1時長為19 s，FT1時長為20 s。試驗中設定檢測步長為25 ms。用本文的故障特征計算方法提取信號的故障特征序列。圖1是對正常信號段NT1提取的細節信號和逼近信號的加權平均峭度特征序列，以及細節信號與逼近信號的故障特征序列。圖2是對信號段FT1提取的細節信號和逼近信號的加權平均峭度序列，以及細節信號與逼近信號的故障特征序列。以下如無特別說明，圖中的Fk Sequence和Gk Sequence分別表示逼近信號和細節信號的加權平均峭度特征序列，Wk Sequence是加權平均均方根特征序列。

圖1 NT1提取的故障特征序列Fig.1 Fault feature sequences extracted from NT1

從圖1可知，正常信號的故障特征序列(Fk Sequence，Gk Sequence和 Wk Sequence)總體上呈現平穩波動趨勢，可是其波動幅度偶爾出現較大但呈現不連續的情況。從圖2可知，故障信號FT1的故障特征序列在未出現故障前呈現平穩波動，但當出現故障后其幅值陡然增長。試驗對其它歷史數據的分析也得到類似的結果，說明本文方法提取的故障特征具有較好的故障敏感性，但正常信號的分析結果，即故障特征序列仍存在序列不平緩，部分正常偶爾波動較大的問題，這使檢測易出現虛警，需要結合一定的判定策略以減少虛警。

圖2 FT1提取的故障特征序列Fig.2 Fault feature sequences extracted from FT1

3.2 故障檢測方法的有效性和實時性驗證

正常信號段NTr1、NTr2、NTr3和故障信號段FTr1、FTr2被用于模擬渦輪泵的實時故障檢測過程，以驗證本文方法的有效性和實時性。

3.2.1 檢測方法的有效性驗證

為驗證方法的有效性，作為試驗對象的信號為NTr1和FTr1，NTr1是時長為16 s的正常信號，FTr2是時長21.0177 s的故障信號。根據對故障信號的試車后數據分析，已知信號在20.5102 s出現故障。圖3是對NTr1故障檢測的結果，圖4是對FTr1故障檢測的結果。

從圖3可知該檢測方法在檢測正常數據過程中沒有出現報警情況，圖4結果顯示檢測方法對信號FTr1檢測，加權平均峭度在20.6 s時報警，加權平均均方根在20.9750 s報警。檢測過程未出現虛警和漏警，說明本文方法在故障檢測中是有效的。

3.2.2 檢測方法的實時性驗證

為分析檢測方法的實時性，用信號段NTr1、NTr2、NTr3、FTr1和FTr2對本文方法進行驗證分析，檢測結果如表1所示。

圖3 故障檢測方法對NTr1檢測的結果Fig.3 The fault detection results of NTr1 with the proposed method

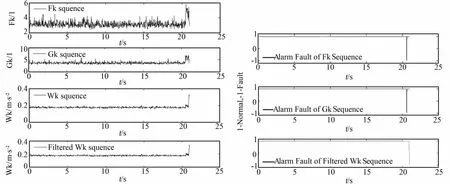
圖4 故障檢測方法對FTr1檢測的結果Fig.4 The fault detection results of FTr1 with the proposed method

從表1可知，在檢測中每步長信號計算時間均比步長時間少，因此不會出現運算時間的累積大于信號時長的情況，能夠實時檢測實時采集的數據。在檢測故障數據時能有效檢測故障，進行故障報警。說明方法有較好的實時性。試驗中，采用給出的故障判別決策后，本文方法在檢測正常數據時未出現虛警，在檢測故障信號時未出現虛警和漏警，說明其在故障檢測中具有較好的準確性。

4 結論

本文提出了一種基于提升小波與RLS的渦輪泵故障檢測方法，通過某型發動機渦輪泵歷史試車的殼體振動加速度信號驗證故障檢測方法。由試驗結果，可得以下結論:1)本文方法能有效檢測發動機渦輪泵的故障，在故障檢測中未出現虛警和漏警，具有良好的準確性和實時性;2)在故障特征計算中采用提升小波進行信號的分解和重構，方法簡潔、計算速度快、原位運算節省存儲空間，提高了運算效率;3)采用RLS算法對故障特征進行濾波，減少了由隨機因素引起的故障特征過大波動，減小虛警和漏警;4)提出了一種故障特征計算提取方法，用提升小波變換對信號進行分解和單支重構，計算逼近信號與細節信號的加權平均均方根、加權平均峭度作為故障特征，故障特征穩定性較好，故障敏感性較強，能有效反映渦輪泵的狀態變化;5)在故障判別策略中，計算當前特征點與其鄰近局部均值的比值，將其與設定的閾值對比，采用連續多次異常則進行特征序列報警，根據多個特征序列報警來判定渦輪泵故障，有效減少了虛警。

表1 檢測五組渦輪泵殼體振動加速度信號的實驗結果Table 1 Fault detection results of 5 groups of vibration acceleration signals of shell of turbopump

本文為渦輪泵的健康監控提供了一種故障檢測方法，對故障檢測與診斷具有一定的意義。然而對于故障檢測方法的軟、硬件系統實現和應用，故障判別策略中的比值閾值的設置和更新調整方面還需進一步研究。

［1］ 陳啟智.液體火箭發動機故障檢測與診斷研究的若干進展［J］.宇航學報，2003，24(1):1-11.

［2］ 夏魯瑞.液體火箭發動機渦輪泵健康監控關鍵技術及系統研究［D］.長沙:國防科學技術大學，2010，1-19.

［3］ 謝光軍，胡海峰，秦國軍，等.液體火箭發動機渦輪泵健康監控系統［J］.國防科技大學學報，2005，27(3):40-44.

［4］ 賀菲.運載火箭故障檢測處理系統軟件研究和實踐［J］.載人航天，2008(2):28-32.

［5］ 彭小輝，劉垠杰，程玉強，等.基于云關聯規則的液體火箭發動機實時故障檢測方法［J］.載人航天，2013，19(3):84-90.

［6］ 張惠軍.液體火箭發動機故障檢測與診斷技術綜述［J］.火箭推進，2004，30(5):40-45.

［7］ 謝光軍，李儉川，胡蔦慶，等.渦輪泵實時故障檢測的多特征參量自適應閾值綜合決策算法［J］.中國機械工程，2005，16(13):1184-1187.

［8］ 謝光軍，胡蔦慶，溫熙森，等.渦輪泵實時故障檢測短數據均值自適應閾值算法［J］.推進技術，2005，26(3):202-205.

［9］ 謝廷峰，劉洪剛，丁偉程，等.液體火箭發動機基于ATA算法的實時故障檢測與報警系統實現［J］.火箭推進，2005，31(6):19-22.

［10］ 洪濤，黃志奇，鐘福利.渦輪泵實時故障檢測的頻段幅值最大值比方法［J］.電子測量與儀器學報，2012，26(1):24-30.

［11］ Xia Lu-Rui，Hu Niao-Qing，Qin Guo-Jun，et al.Typical fault diagnosis method for high-speed turbopump of Liquid Rocket Engine［C］//Systems and Control in Aerospace and Astronautics，2008.ISSCAA 2008.2nd International Symposium on Shexzhen，2008:1-5.

［12］ 羅俊，何立明，陳超.基于小波分形和一類辨識的航空發動機故障診斷［J］.推進技術，2007，28(1):82-85.

［13］ 胡廣書.現代信號處理教程［M］.北京:清華大學出版社，2004:358-370.

［14］ 張賢達.現代信號處理［M］.北京:清華大學出版社，2002:206-213.

［15］ Sweldens W.The lifting scheme:a construction of second genneration wavelets［J］.SIAM Journal on Mathematical Analysis，1997，29(2):511-546.

［16］ Sweldens W.The lifting scheme:a custom-design construction of biorthogonal wavelets［J］.Applied and Computational Harmonic Analysis，1996，3(2):186–200.

［17］ 石敏，吳正國，尹為民.基于RLS算法的時變諧波檢測［J］.電工技術學報，2005，20(1):50-53.

［18］ He Zhengyou，Fu Ling，Lin Sheng，et al.Fault detection and classification in EHV transmission line based on wavelet singular entropy［J］.IEEE Transaction on Power Delivery，2010，25(4):2156-2163.

［19］ 樊春玲，金志華，田蔚風.基于小波模糊神經網絡的陀螺儀故障診斷技術［J］.上海交通大學學報，2003，37(1):141-144.

［20］ 葉昊，王桂增，方崇智.一種基于小波變換的導彈運輸車輛故障診斷方法［J］.自動化學報，1998，24(3):301-306.