臨界雷諾數下帶人工水線斜拉索氣動性能研究

杜曉慶，張 燁，顧 明

(1.上海大學 土木工程系，上海 200072;2.同濟大學 土木工程防災國家重點實驗室，上海 200092)

自Hikami等［1］首先報道了斜拉橋拉索的風雨激振現象以來，20多年內，世界各地斜拉橋拉索在風雨共同作用下發生過大幅振動［2-5］。該振動會嚴重危害拉索與斜拉橋的安全。因此成為重點關注問題之一。雖通過現場實測、風洞試驗與理論分析等方法對拉索風雨激振現象進行研究，并取得不少研究成果，但對拉索風雨激振的發生機理尚無確切認識。

在風洞中對拉索節段模型進行風洞試驗是研究拉索風雨激振特性與發生機理的主要手段之一。通過對帶人工水線拉索節段模型進行的測力或測壓試驗［6-8］，可獲得作用在拉索模型所受的氣動力，并進一步基于準定常假定建立分析拉索風雨激振理論模型［9-12］。

有研究認為［2-3］，拉索發生風雨激振的風速范圍為6～18 m/s，拉索直徑12～20 cm，拉索發生風雨激振的雷諾數(Re數)在6×104～2.0×105之間，處于亞臨界區。但隨著斜拉橋跨度的增大，拉索直徑有增大趨勢，丹麥Oresund High橋的拉索直徑已達到250 mm［13］。因此拉索發生風雨激振時的雷諾數會進入臨界區(2.0×105＜Re＜5 ×105［14］)。但以往拉索模型測力或測壓試驗的Re數范圍為 1 ×104～1.2 ×105［6-8］，研究僅限于亞臨界Re數范圍內。當Re數進入臨界區后，拉索的氣動性將發生很大變化。

基于此，本文在臨界Re數下，對帶上人工水線的三維拉索節段模型進行同步測壓風洞試驗研究。通過風洞試驗，系統測量上水線在不同位置時，三維拉索節段模型表面的風壓分布規律;得到三維拉索模型氣動力系數后分析臨界Re數下拉索的氣動穩定性。本文結果可為進一步建立臨界Re數下拉索風雨激振理論模型提供基礎。

1 試驗裝置及試驗工況

1.1 試驗模型及參數

為在拉索模型表面布置足夠測壓點，用放大的拉索節段模型。該模型采用有機玻璃材料，直徑350 mm，模型全長3.5 m，見圖1。模型直徑約為實際拉索直徑的2～3倍。為達到Re數的相似，試驗風速設為5 m/s和10 m/s，分別對應 Re 數為1.17 ×105和2.34 ×105。前者Re數處在亞臨界區內，后者Re數則處在臨界區內。試驗采用兩種不同大小的圓弧形上水線模型，水線模型同樣采用有機玻璃材料，見圖2。在拉索模型的四個截面上共布置176個測壓點，本文結果所在截面的測壓點布置見圖3，角度θu表示上水線位置，角度θcyl表示測壓點位置。

圖1 試驗裝置及模型照片Fig.1 Photo of test set-up and model

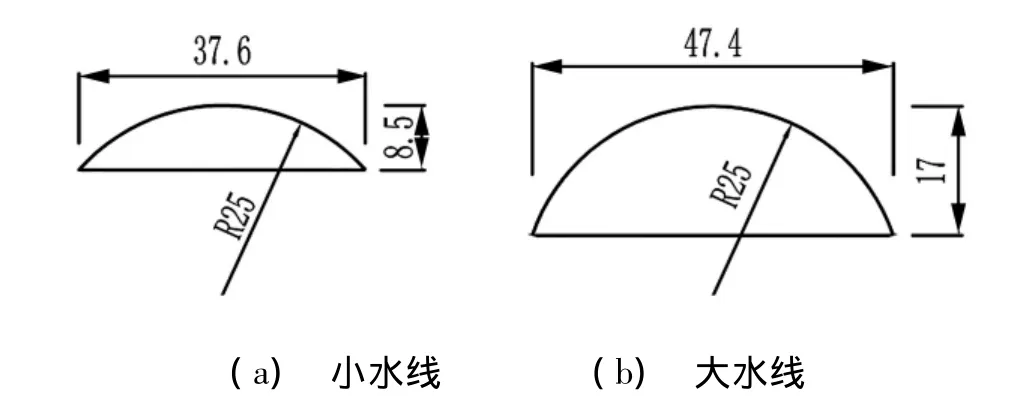
圖2 人工水線形狀尺寸(單位:mm)Fig.2 Sizes of artificial rivulets(unit:mm)

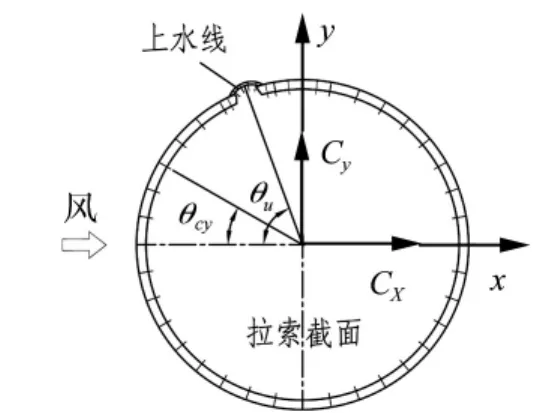
圖3 測點布置圖Fig.3 Arrangement of pressure taps

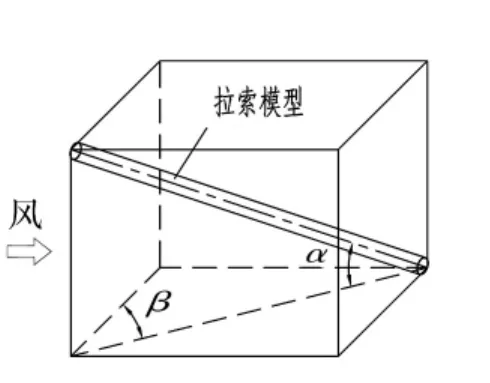
圖4 拉索模型傾角與風向角定義Fig.4 Cable inclined angle and wind angle

拉索模型通過兩端鋼支架以固定傾角α=30°支撐在風洞轉盤上。為減小拉索模型振動，用張緊鋼絲作為纖繩扶持鋼支架。風洞轉盤可調節拉索模型風向角β。拉索模型傾角α及風向角β的定義見圖4。拉索模型上端伸至風洞頂板，以減小拉索模型端部流體分離對試驗結果影響。在風向角為0°時，拉索模型下端安裝導流板;轉過一定偏角時，由于模型下端均處在測點尾流區內，模型下端流體分離對試驗結果影響不大，因而下端未安裝導流板。

1.2 試驗工況

本文拉索人工降雨試驗表明［15］:拉索傾角為30°左右，風向角為30°～35°附近時，最易發生風雨激振，且風向角對拉索風雨激振影響大于傾角影響。因此在進行測壓試驗時，應重點研究風向角對拉索氣動性能的影響。試驗時拉索傾角α固定在30°，風向角β則分別為 0°、25°、35°、40°和 45°。限于篇幅，本文只給出風向角為0°和35°的試驗結果。

1.3 風洞及測試設備

風洞試驗在同濟大學土木工程防災國家重點實驗室TJ-3大氣邊界層風洞均勻流風場中進行。該風洞為豎向回流式低速風洞，試驗段寬15 m、高2 m、長14 m。試驗段底板的轉盤直徑3.8 m。試驗風速范圍從0.2～17.6 m/s連續可調。流場性能良好，湍流度約為2%、平均氣流偏角小于0.2°。

由美國Scanivalve掃描閥公司量程為±254 mm和±508 mm水柱的DSM3000電子式壓力掃描閥系統、PC機、自編信號采集及數據處理軟件組成風壓測量、記錄及數據處理系統。采樣時間25.6 s;采樣點數8000;采樣頻率 312.5 Hz。

2 試驗結果及分析

本文試驗結果在Re數為2.34×105時，在帶小水線拉索模型上測得。文獻［16］分析了三維光拉索模型(即未帶水線拉索模型)與本文相同試驗條件下所得平均風壓與平均氣動力特性表明，因受湍流度影響(本文試驗的來流湍流度約2%)，在Re=2.34×105時，光拉索模型表面的平均風壓系數分布呈現臨界雷諾數下的圓柱繞流特征:尾流區變窄，拉索表面分離點在圓柱體背風面，拉索模型上下側風壓系數出現不對稱分布(單分離泡現象)。此外，文獻［18］進一步研究了相同試驗條件下三維光拉索的脈動風壓和脈動風力特性表明，Re=2.34 ×105時，風向角為 0°和 45°的三維拉索尾流區出現隨機的漩渦脫落，呈現出典型的臨界區圓柱繞流特征。因此，在本文試驗條件下，Re=2.34×105時，拉索模型已處在臨界雷諾數區。

2.1 風向角為0°

2.1.1 平均氣動力系數

坐標軸和氣動力方向的定義見圖3。將測得的平均風壓沿拉索周向積分，并向坐標軸x和y方向投影，即可得作用在拉索模型上的平均氣動力系數Cx和Cy。

圖5 為風向角 β=0°、Re=2.34 ×105時，拉索平均氣動力系數隨上水線位置θu的變化曲線。為與亞臨界雷諾數時的情況作比較，圖中列出文獻［17］中Re=1.17×105時的拉索平均氣動力系數。風向角β=0°時，拉索模型為二維的。而斜拉索發生風雨激振時均處于三維狀態，三維拉索的氣動性能較二維拉索復雜得多。為更深入理解上水線對拉索氣動性能的影響規律，本文先對二維拉索模型的試驗結果進行分析。

從圖5可見，在兩種雷諾數條件下，上水線的出現均完全改變了拉索的氣動性能，且拉索的氣動力系數對上水線位置非常敏感。與亞臨界雷諾數時的氣動力曲線相比，臨界雷諾數下平均氣動力曲線形態有顯著差異，尤其平均升力系數Cy。當Re=1.17×105時(即雷諾數處在亞臨界區)，平均氣動力系數在θu=60°附近發生突然變化，升力系數Cy從0.35突然下降至-0.14，而阻力系數Cx則從0.60 增大至0.94。拉索氣動力系數的這種突變是拉索發生風雨激振的主要原因。而當Re=2.34×105時(即雷諾數處在臨界區)，平均升力系數Cy分別在上水線θu=20°和65°附近經歷兩次逐漸減小過程。與亞臨界區相比，臨界區內升力系數的下降幅度相近，但下降過程則較緩慢。

2.1.2 平均風壓系數

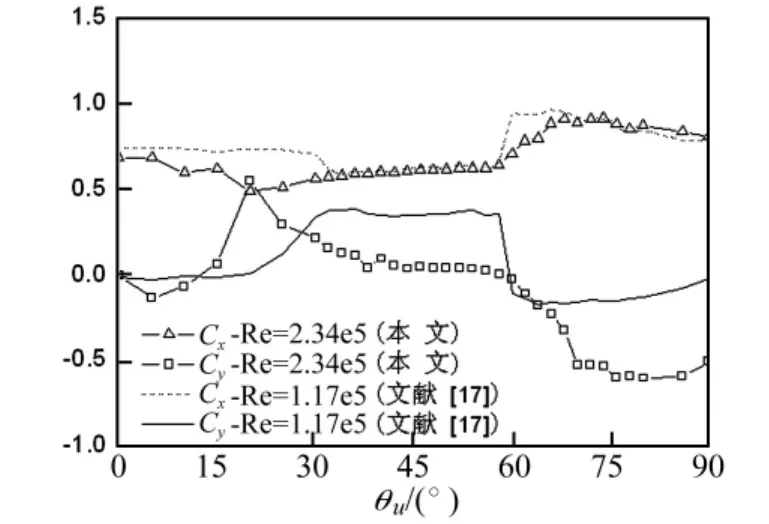
圖5 帶水線拉索平均氣動力系數(β=0°)Fig.5 Mean aerodynamic force coefficients of cable against rivulet positions(β =0°)

為進一步分析上水線位置對二維拉索氣動性能影響，上水線在典型位置時，拉索模型表面平均風壓系數分布情況見圖6。由圖6知，上水線處在不同位置，拉索表面平均風壓系數的分布差異較大。θu=0°時，帶上水線拉索模型的負風壓系數絕對值與文獻［16］中光拉索相比有所減小。θu=20°時，在上水線后局部區域拉索表面測點(θcyl在45°～110°間測點)的負風壓系數絕對值突然增大，而拉索其它部位的風壓系數則變化不大，導致圖5中θu=20°所對應的平均升力系數Cy達最大值0.55。當上水線位置θu從20°變化至60°時，上水線后局部測點的風壓系數與θu=20°相比，受水線影響的測點區域逐漸變小(θcyl在50°～90°間測點)，從而使圖5 中的升力系數Cy逐步減小。當θu=70°時，上水線附近測點的風壓系數絕對值突然增大現象消失，而拉索下側(無水線一側)測點的負風壓系數絕對值則增大，導致圖5中相應位置的平均升力系數Cy減小至-0.53。

圖6中拉索平均風壓分布隨上水線位置的變化，可能與拉索上表面流體分離及再附現象有關。上水線的存在影響拉索上側表面流體分離及分離流再附。當上水線位于20°～60°之間時，流體在上水線處發生分離，在上水線后側的拉索表面發生再附，最后在拉索背風側再次發生分離。而當上水線位于70°后，不再發生分離流的再附。

2.2 風向角為35°

2.2.1 平均氣動力系數

風向角β=35°時，拉索模型為三維。三維光拉索的氣動性能較二維拉索更復雜。圖7為風向角β=35°、Re=2.34 ×105時，拉索平均氣動力系數隨上水線位置θu的變化曲線及Re=1.17×105時的拉索平均氣動力系數［17］。

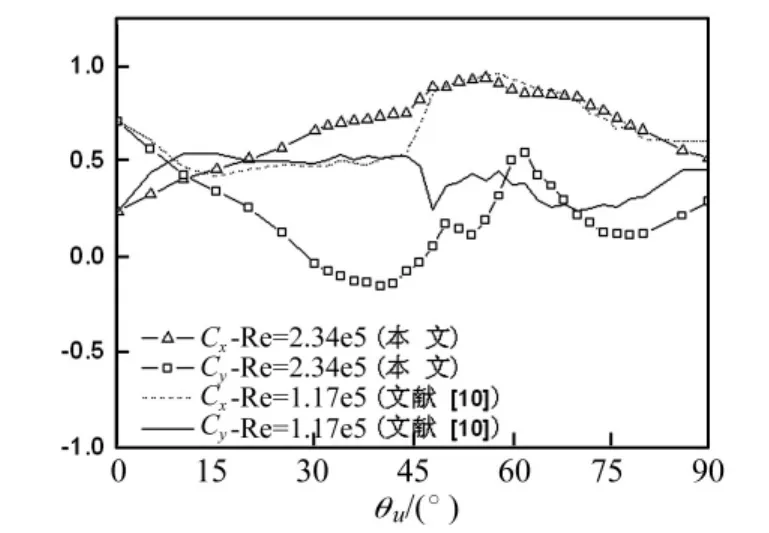
圖7 帶水線拉索平均氣動力系數(β=35°)Fig.7 Mean aerodynamic force coefficients of cable against rivulet positions(β =35°)

由圖7可見，與亞臨界雷諾數的結果相比，臨界雷諾數時的氣動力系數無論曲線形態或數值上均有很大差異。Re=2.34 ×105時，升力系數Cy在 θu=0°時達到0.71;隨著 θu的增大，升力系數Cy逐漸減小，并在 θu=40°達最小值 -0.15;當上水線位于 θu=62°時，升力系數逐漸增大到峰值0.55;而隨著θu繼續增大至76°，升力系數又逐漸減小至0.12。

2.2.2 平均風壓系數

風向角 β =35°、Re=2.34 ×105時，上水線位置對三維拉索模型表面平均風壓分布影響見圖8。由圖8可見，隨著來流風向角從0°增大至35°，拉索表面停滯點位置從0°移至340°附近，停滯點平均風壓系數小于1。當θu=0°時，與文獻［16］中光拉索表面風壓分布相比，在拉索上側局部測點(θcyl在45°～90°之間)的負風壓系數絕對值增大，而拉索其它測點負風壓系數絕對值則減小，從而使拉索模型承受較大升力，平均升力系數Cy達0.71(圖7)。當θu=40°時，在上水線附近測點(θcyl=45°附近)和拉索下側部分測點(θcyl在 230°～300°之間)均出現絕對值較大的負風壓系數。說明上水線在此位置時，水線不但影響拉索上側表面風壓，也影響拉索下側表面風壓分布。當θu=62°時，上水線對拉索表面測點影響范圍較大，θcyl在70°～135°之間的表面測點負風壓系數絕對值均保持較高數值，使拉索受較大升力系數Cy作用。而當上水線位于θu=76°時，拉索表面負風壓系數分布平緩，拉索所受升力較小。

圖8 帶上水線拉索平均風壓系數分布 (β=35°，Re=2.34×105)Fig.8 Distribution of wind pressure on cable model with upper rivulet，(β =35°，Re=2.34 ×105)

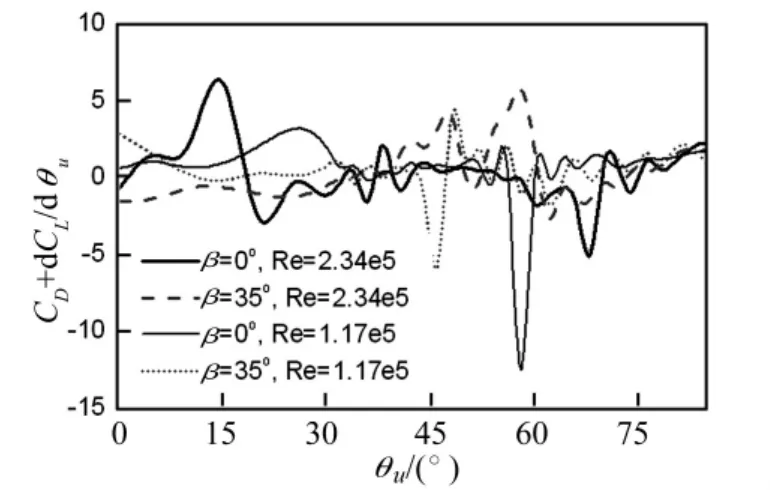
圖9 CD+dCL/dθu隨水線位置的變化Fig.9 Variations of the function CD+dCL/dθuwith rivulet positions

2.3 穩定性分析

風向角分別為0°和35°、雷諾數分別為1.17×105和2.34 ×105時，氣動力系數函數CD+dCL/dθu隨上水線位置的變化曲線見圖9。據Den Hartog馳振失穩判據，函數CD+dCL/dθu＜0是發生馳振失穩的必要條件。由準定常假定，CD+dCL/dθu＜0區域為拉索發生風雨激振的失穩區。從圖9可見，在兩種雷諾數下，拉索均存在CD+dCL/dθu＜0的失穩區。但隨著雷諾數從亞臨界區(Re=1.17×105)增大至臨界區(Re=2.34×105)，函數CD+dCL/dθu負值的絕對值減小，失穩區對應的水線位置θu增大，即拉索發生失穩的可能性降低，失穩發生在較高的水線位置。此外，同一種雷諾數下，隨著風向角的增大，拉索發生失穩的可能性降低，失穩區對應的水線位置減低。

3 結論

本文通過風洞試驗，在臨界雷諾數下，通過研究帶上水線拉索模型的氣動性能，測量不同風向角下拉索表面的風壓分布，得到作用在拉索上的氣動力系數，并對臨界雷諾數下拉索氣動穩定性進行分析，結論如下:

(1)拉索表面平均風壓分布對上水線位置非常敏感。不同位置的上水線會改變拉索表面的流體分離與分離流再附，導致拉索表面平均風壓分布隨上水線位置的改變而變化劇烈。

(2)與亞臨界區相比，臨界雷諾數下的氣動力系數隨水線位置變化的曲線形態差異顯著。基于準定常假定，在臨界雷諾數下，拉索仍有發生風雨激振的可能，但較亞臨界區會有所降低。

(3)風向角是影響拉索氣動性能的又一重要因素，風向角會改變拉索表面風壓、氣動失穩可能性與失穩區域。

［1］Hikami Y，Shiraishi N.Rain-wind induced vibrations of cables stayed bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1988，29(1-3):409-418.

［2］ Matsumoto M，Shiraishi N.Rain-wind induced vibrations of cablesofcable-stayed bridge［J］. JournalofWind Engineering and Industrial Aerodynamics，1992，43(1-3):2011-2022.

［3］顧 明，劉慈軍，羅國強，等.斜拉橋拉索的風(雨)激振及控制［J］.上海力學，1998，19(4):283-288.

GU Ming，LIU Ci-jun，LOU Guo-qiang，et al.Rain-wind induced vibration of cables on cable-stayed bridges and its control［J］.Shanghai Journal of Mechanics，1998，19(4):283-288.

［4］Main J A，Jones N P.Full-scale measurements of stay cable vibration［A］.Wind engineering into the 21stcentury［C］.Balkema，Rotterdam，1999:963-970.

［5］Ni Y Q，Wang X Y，Chen Z Q.Field observations of rainwind-induced cable vibration in cable-stayed Dongting lake bridge［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95(5):303-328.

［6］Gu M，Lu Q.Theoretical analysis of wind-rain induced vibration of cables of cable-stayed bridges［J］.Journal of Wind Engineering，2001，89:125-128.

［7］ Matsumoto M，Yagi T，Saka S，et al.Steady wind force coefficients of inclined stay cables with water rivulet and their application to aerodynamics［J］.Wind and Structures，2005，8(2):107-120.

［8］ Xu Y L，Li Y L，Shum K M，et al.Aerodynamic coefficients of inclined circular cylinders with artificial rivulet in smooth flow［J］.Advances in Structural Engineering，2006，9(2):265-278.

［9］Yamaguchi H.Analytical study on growth mechanism of rain vibration of cable［J］.Journal of Wind Engineering and Industrial Aerodynamics，1990，33(1-2):73-80.

［10］ Xu Y L.Wang L Y.Analytical study of wind-rain-induced cable vibration:SDOF model［J］. JournalofWind Engineering and Industrial Aerodynamics，2003，91(1-2):27-40.

［11］ Gu M，Du X Q，Li S Y.Experimental and theoretical simulations on wind-rain induced vibration of 3-D rigid stay cables［J］.Journal of Sound and Vibration，2009，320(1-2):184-200.

［12］ Gu M.On wind-rain induced vibration of cables of cablestayed bridges based on quasi-steady assumption［J］.Journal of Wind Engineering and Industrial Aerodynamics，2009，97(7-8):381-391.

［13］ Larose G L，Smitt L W.Rain/wind induced vibrations of parallel stay cables［A］.IABSE conference［C］.Sweden，1999，301-310.

［14］ Simiu E，Scanlan R H.Wind effects on structures［M］.John Wiley＆ Sons，Inc，1996.

［15］ Gu M，Du X Q.Experimental investigation of rain-windinduced vibration of cables in cable-stayed bridges and its mitigation［J］.Journal of Wind Engineering and Industrial Aerodynamics，2005，93(1):79-95.

［16］杜曉慶，顧 明.臨界雷諾數下斜拉橋拉索的平均風壓和風力特性［J］.空氣動力學學報，2010，28(6):639-644.

DU Xiao-qing，GU Ming.Wind pressure distributions and aerodynamic characteristics of stay cables in the critical Reynolds number regime［J］.Acta Aerodynamica Sinica，2010，28(6):639-644.

［17］顧 明，杜曉慶.帶人工雨線的斜拉橋拉索模型測壓試驗研究［J］.空氣動力學學報，2005，23(4):419-424.

GU Ming，DU Xiao-qing.Testing study on wind pressure distributions of stayed cables with an artificial rivulet［J］.Acta Aerodynamica Sinica，2005，23(4):419-424.

［18］杜曉慶，顧 明.斜置拉索表面脈動風力特性研究［J］.振動與沖擊，2012，31(4):139-144.

DU Xiao-qing，GU Ming.Characteristics of fluctuating forces on inclined stay cable［J］.Journal of Vibration and Shock，2012，31(4):139-144.