考慮車輪-路面接觸長(zhǎng)度的橋頭跳車動(dòng)力荷載分析

丁 勇，諸葛萍，謝 旭，李 輝，黃劍源

(1.寧波大學(xué) 土木工程系，寧波 315211;2.浙江大學(xué) 土木工程系，杭州 310027)

近年來(lái)，橋梁結(jié)構(gòu)在車輛荷載作用下的破壞情況經(jīng)常發(fā)生，尤其在橋頭跳車時(shí)，車輛荷載的動(dòng)力效應(yīng)更加顯著，因此出現(xiàn)較多橋頭跳車所致橋臺(tái)、橋面板、伸縮縫、橋頭搭板破壞［1］(圖 1)。

作為橋梁、搭板、橋頭路面設(shè)計(jì)的原始依據(jù)［2-4］，車輛經(jīng)過(guò)橋頭時(shí)的動(dòng)力荷載非常重要。該動(dòng)力荷載主要作用在橋梁端部，按中國(guó)橋梁規(guī)范［5］，可采用車輛荷載的局部沖擊系數(shù)(0.3)考慮其影響，美國(guó)橋梁規(guī)范將橋面接縫處的沖擊系數(shù)定為 0.75，其余為 0.33［6］，其他國(guó)家則未對(duì)橋頭跳車沖擊荷載做專門規(guī)定［7］。

圖1 橋頭橋面板開裂Fig.1 Crack of the bridge deck at the bridge-head

張麗芳等［2，8-9］對(duì)橋頭跳車問(wèn)題進(jìn)行的研究，內(nèi)容涉及車輛作用下橋梁、橋頭搭板等結(jié)構(gòu)的動(dòng)力響應(yīng)。但橋頭跳車動(dòng)力荷載的相關(guān)研究較少。目前由實(shí)驗(yàn)確定該動(dòng)力荷載較困難亦較昂貴［10-11］，主要研究集中于理論分析。劉曉明等［12］采用7自由度車輛理論模型分析了橋頭搭板平順過(guò)渡情況下車輛動(dòng)力荷載;Ding等［13］采用4自由度車輛理論模型及簡(jiǎn)支梁橋理論模型，分析了車軸動(dòng)力荷載;丁勇等［14］采用考慮滾動(dòng)軌跡的圓盤車輪模型，計(jì)算了橋頭錯(cuò)臺(tái)跳車時(shí)的動(dòng)荷載，避免了以往單點(diǎn)車輪模型經(jīng)錯(cuò)臺(tái)時(shí)的突跳。但該研究未考慮輪胎與地面的接觸長(zhǎng)度，可能會(huì)高估跳車動(dòng)力荷載。

本文提出考慮車輪與路面接觸長(zhǎng)度的圓盤車輪模型，結(jié)合車輛的三維有限元模型及相應(yīng)的動(dòng)力學(xué)分析方法，分析橋頭跳車時(shí)的車輪動(dòng)力荷載，并探討該荷載的影響因素。

1 車輪動(dòng)力荷載計(jì)算方法

1.1 橋頭錯(cuò)臺(tái)模型

橋頭錯(cuò)臺(tái)是產(chǎn)生跳車的重要因素，其產(chǎn)生原因由橋臺(tái)與路堤剛度不同導(dǎo)致的沉降差，雖設(shè)置橋頭搭板后可減小不均勻沉降影響，但錯(cuò)臺(tái)現(xiàn)象仍存在(圖2)。據(jù) White等［1］在美國(guó)的調(diào)查，橋頭錯(cuò)臺(tái)現(xiàn)象較常見，最大高差達(dá)38 mm，因此本文采用橋頭錯(cuò)臺(tái)作為跳車的激勵(lì)源。

1.2 車輛振動(dòng)方程

為確定車輪動(dòng)力荷載，需分析車輛經(jīng)過(guò)橋梁時(shí)的振動(dòng)，以往研究常采用多自由度車輛振動(dòng)理論方程組［2，8-9，12-13］。為避免復(fù)雜的理論分析方法，本文采用有限單元法模擬車輛［14-15］。如典型20 t三軸載重車輛三維有限元模型見圖3。

該模型由三種單元組成(彈簧-阻尼單元、集中質(zhì)量單元、剛性梁?jiǎn)卧?，包括37個(gè)單元，25個(gè)節(jié)點(diǎn)，計(jì)算參數(shù)見表1。

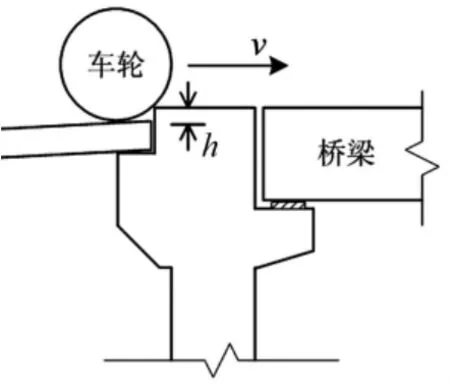
圖2 橋頭錯(cuò)臺(tái)Fig.2 The staggered platform at bridge-head

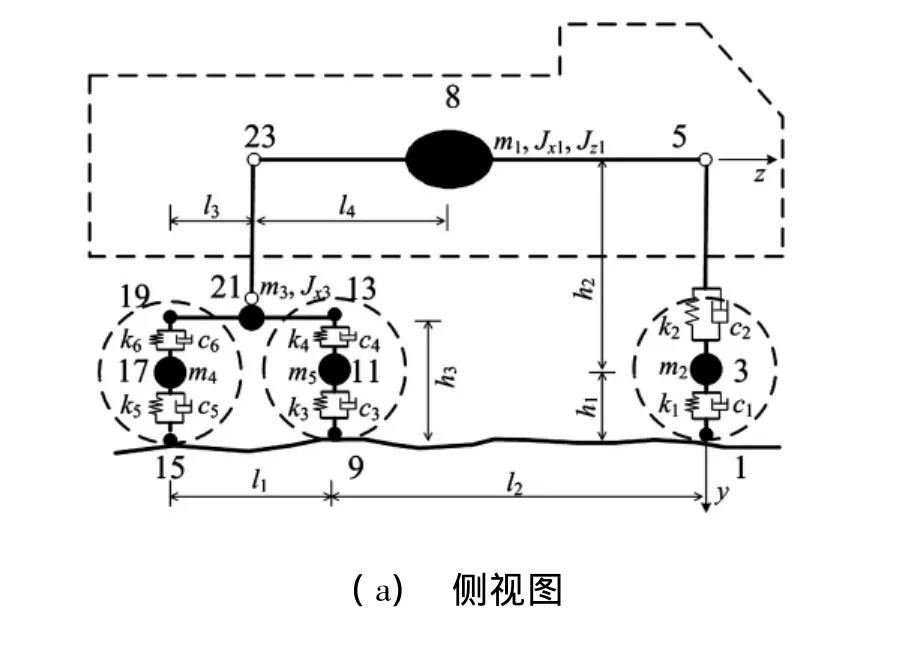
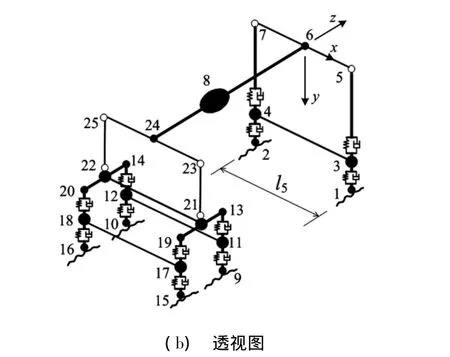
圖3 車輛三維有限元模型Fig.3 3-D FEM model of vehicle

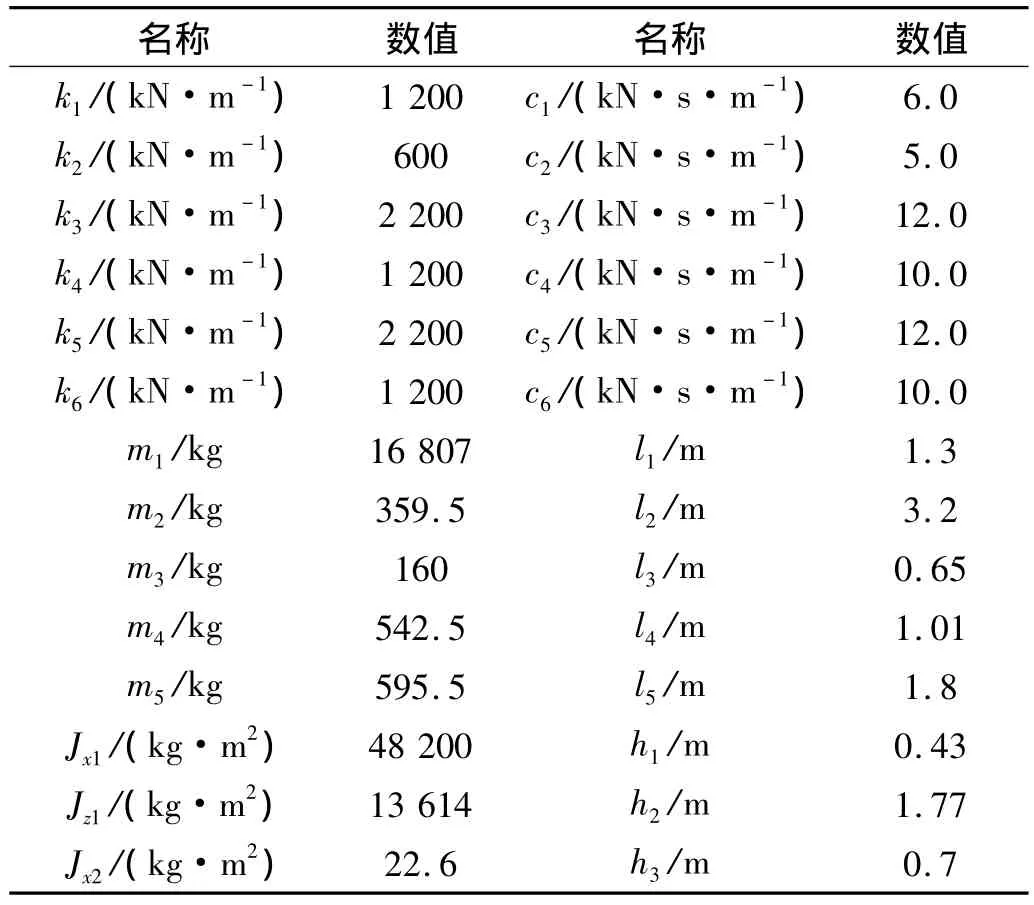
表1 車輛計(jì)算參數(shù)［16］Tab.1 Parameters of vehicle

單元組集后，得車輛振動(dòng)方程為:

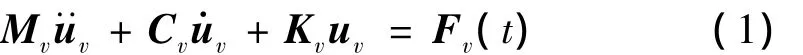
其中:uv為節(jié)點(diǎn)位移矢量;Mv、Cv、Kv分別為質(zhì)量、阻尼、剛度矩陣;Fv為車輛所受荷載;t為時(shí)間。式(1)可利用Newmark法在時(shí)間域內(nèi)積分求解，車輪與路(橋)面的接觸點(diǎn)需給定位移或荷載，其數(shù)值與車輪軌跡有關(guān)，因此需確定橋頭跳車時(shí)輪底節(jié)點(diǎn)軌跡。

1.3 不計(jì)車輪－路面接觸長(zhǎng)度的車輪運(yùn)動(dòng)軌跡分析

分別研究車輛上、下橋跳車時(shí)的車輪軌跡，以確定式(1)的邊界條件。考慮車輪滾動(dòng)影響，采用圓盤模型［14］描述其運(yùn)動(dòng)。分析車輪變形較小，不計(jì)車輪與路面的接觸長(zhǎng)度情況。

1.3.1 上橋跳車

如圖4所示，當(dāng)車輪以速度v過(guò)橋頭錯(cuò)臺(tái)時(shí)，繞頂點(diǎn)B滾動(dòng)。輪底由A點(diǎn)升高到B點(diǎn)，其運(yùn)動(dòng)軌跡為曲線2，該曲線在B點(diǎn)與水平線相切。設(shè)曲線2為圓弧線，則其與曲線1(B為圓心，R為半徑的圓弧)平行，因此輪底A點(diǎn)運(yùn)動(dòng)軌跡(高度)為:

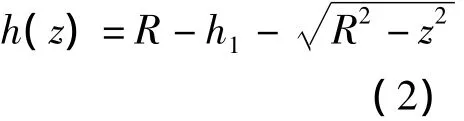
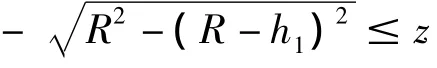
1.3.2 下橋跳車

如圖5(a)所示，車輪下橋通過(guò)錯(cuò)臺(tái)時(shí)，若速度較低，車輪將繞頂點(diǎn)D滾動(dòng)，輪軸由O點(diǎn)轉(zhuǎn)至O'點(diǎn)，輪軸離地面距離為:

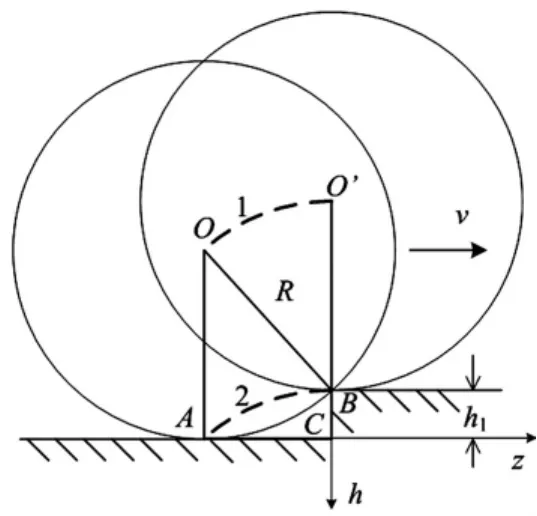
圖4 上橋跳車時(shí)的車輪軌跡Fig.4 Rolling trace of the tire getting on the bridge

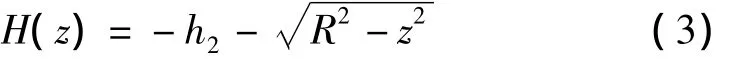
其中:h2為錯(cuò)臺(tái)高度。由此可得輪軸加速度為:

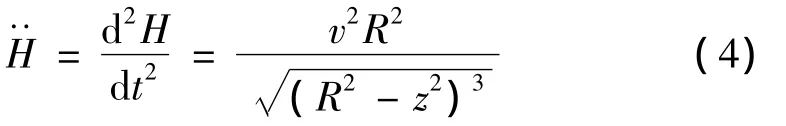
其中:v為車輛速度。

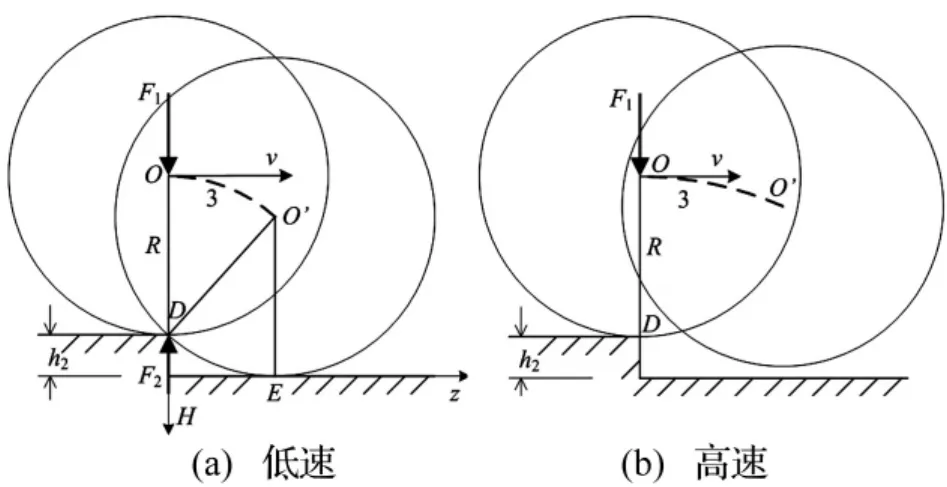
圖5 下橋跳車時(shí)的車輪軌跡Fig.5 Rolling trace of the tire getting off the bridge

為在車輛振動(dòng)的有限元分析中得到上述輪軸加速度，可給定路面對(duì)輪底的荷載:

其中:F1為輪軸的車體重力，maxis為輪軸質(zhì)量。

車速較高時(shí)，車輪將出現(xiàn)脫離錯(cuò)臺(tái)的騰空現(xiàn)象，如圖5(b)所示。此時(shí)輪底荷載為0，由式(5)可得:

設(shè)車輪騰空時(shí)臨界速度為vcr，將式(4)代入式(6)得:

臨界速度為:

模擬車輛下橋通過(guò)錯(cuò)臺(tái)時(shí)，無(wú)論高速或低速情況，均將F2作為給定的輪底荷載邊界條件，代入車輛振動(dòng)方程(1)，積分可得車輛模型中各節(jié)點(diǎn)位移、速度、加速度。

1.4 考慮車輪－路面接觸長(zhǎng)度的車輪運(yùn)動(dòng)軌跡分析

對(duì)充氣輪胎等剛度較小的車輪，其與路面間存在近似矩形的接觸面積，從側(cè)面看，輪胎與地面間存在一接觸長(zhǎng)度。以下分析此時(shí)的車輪運(yùn)動(dòng)軌跡。

1.4.1 上橋跳車

考慮接觸長(zhǎng)度時(shí)，車輪上橋前、后位置如圖6所示，因車輪半徑較變形大得多，故設(shè)未接觸部分仍保持圓形，且半徑不變。接觸長(zhǎng)度為L(zhǎng)，其值可由輪胎壓縮量計(jì)算獲得。

車輪上橋時(shí)，輪底從A點(diǎn)逐漸升高到A'點(diǎn)，并與水平線相切，設(shè)其運(yùn)動(dòng)軌跡仍為圓弧曲線(曲線2)，則其半徑與圓心位于B'點(diǎn)的圓弧曲線(曲線1)相等，據(jù)幾何關(guān)系推導(dǎo)得:

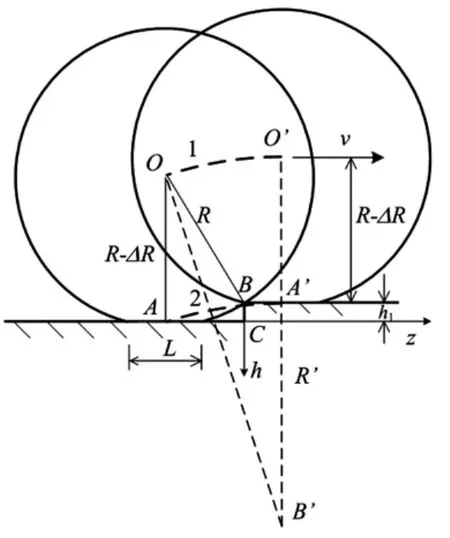
圖6 考慮接觸長(zhǎng)度時(shí)上橋跳車軌跡Fig.6 Rolling trace of the tire getting on the bridge considering the contact length

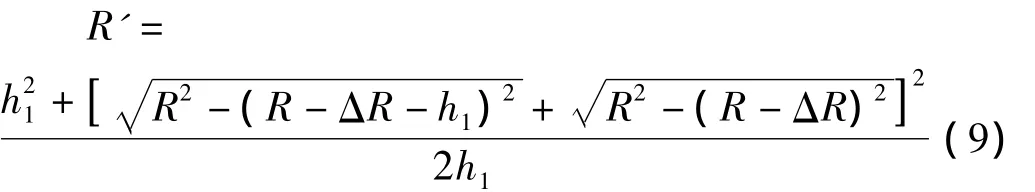
其中:R'為輪底軌跡等效圓弧半徑，ΔR為靜力狀態(tài)下輪胎壓縮量。

由此可得輪底A點(diǎn)距地面高度為:

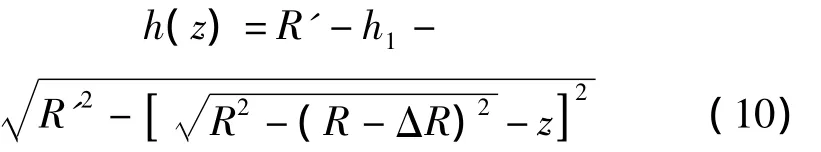
其中:

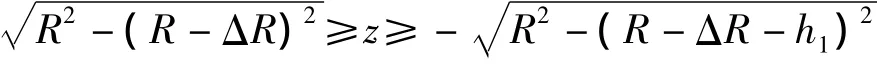
h(z)即為式(1)的給定輪底位移。不計(jì)輪胎變形，等效圓弧半徑R'即為輪胎半徑R，式(10)退化為式(2)。

1.4.2 下橋跳車

考慮接觸長(zhǎng)度時(shí)，車輪下橋前、后位置如圖7所示。設(shè)未接觸部分仍為圓形，半徑不變。車速較低時(shí)，輪軸將由O點(diǎn)逐漸降低到O'點(diǎn)。設(shè)其間的運(yùn)動(dòng)軌跡仍為圓弧曲線(曲線3)，并在O點(diǎn)與水平線相切，因此其圓心為D'，圓弧半徑R'可由幾何關(guān)系推導(dǎo):

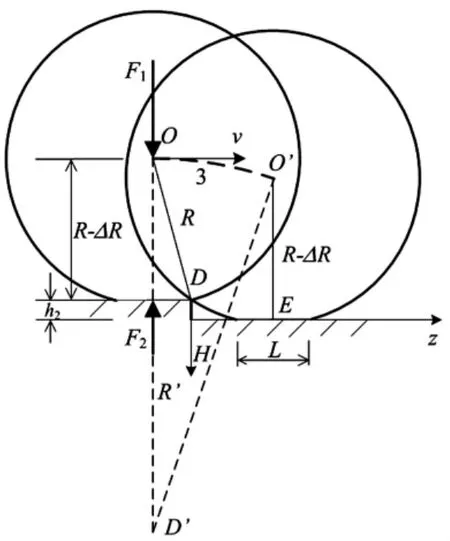
圖7 考慮接觸長(zhǎng)度時(shí)的下橋跳車軌跡Fig.7 Rolling trace of the tire getting off the bridge considering the contact length

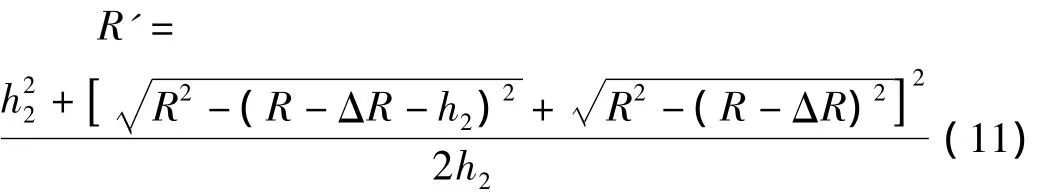
由此可得，跳車過(guò)程中輪軸O離地面高度為:

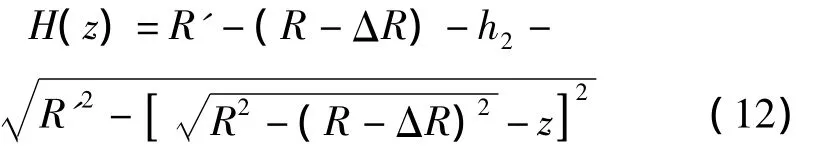
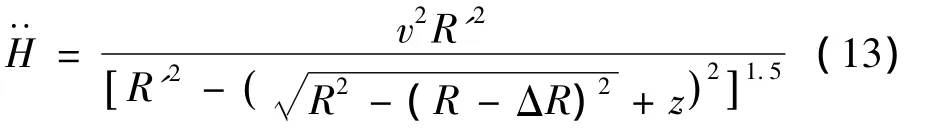
為在車輛振動(dòng)有限元分析中得到上述輪軸加速度，仍給定路面對(duì)輪底荷載，其值由式(5)求得。

車速較高時(shí)，車輪將出現(xiàn)脫離錯(cuò)臺(tái)的騰空現(xiàn)象，此時(shí)輪底所受路面荷載為0，將式(13)代入式(6)，得對(duì)應(yīng)的車速為:

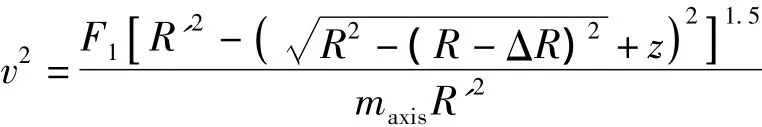
若下橋跳車開始時(shí)，車輛即達(dá)到臨界速度，則:

不計(jì)輪胎變形時(shí)，等效圓弧半徑R'即為輪胎半徑R，式(14)退化為式(8)。

實(shí)際模擬車輛下橋跳車時(shí)，無(wú)論高速或低速情況，均將F2作為給定的輪底荷載邊界條件，代入式(1)，積分可得車輛模型中各節(jié)點(diǎn)位移、速度、加速度。

1.5 車輪動(dòng)力荷載計(jì)算

求出車輛節(jié)點(diǎn)位移、速度后，由輪胎位置的彈簧-阻尼單元得車輪豎向動(dòng)力荷載為:

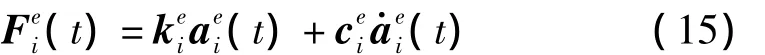
2 算例與討論

對(duì)圖3的典型載重車輛，利用上節(jié)方法求解車輛通過(guò)橋頭錯(cuò)臺(tái)前后的動(dòng)力荷載，積分步長(zhǎng)小于0.001 s，輪胎半徑為0.43 m。由于本文主要討論橋頭沉降錯(cuò)臺(tái)導(dǎo)致的沖擊荷載，故不計(jì)路面粗糙度、橋梁振動(dòng)影響，并假設(shè)橋梁足夠長(zhǎng)，上、下橋頭跳車互不影響。

2.1 考慮輪胎－路面接觸長(zhǎng)度時(shí)車輪動(dòng)力荷載特征

車輛以速度30 km/h通過(guò)10 mm高橋頭錯(cuò)臺(tái)為例，分析跳車時(shí)車輪動(dòng)力荷載特征。

為說(shuō)明考慮輪胎-路面接觸長(zhǎng)度影響，分別采用三種假定計(jì)算車輪動(dòng)荷載:① 將車輪視為一個(gè)點(diǎn);②考慮車輪半徑，用圓盤車輪模型;③ 采用圓盤車輪模型，同時(shí)計(jì)及輪底與路面接觸段，接觸長(zhǎng)度由輪胎壓縮量計(jì)算得到，圖3車輛對(duì)應(yīng)的輪底接觸長(zhǎng)度見表2，接觸長(zhǎng)度計(jì)算值與實(shí)驗(yàn)值接近。

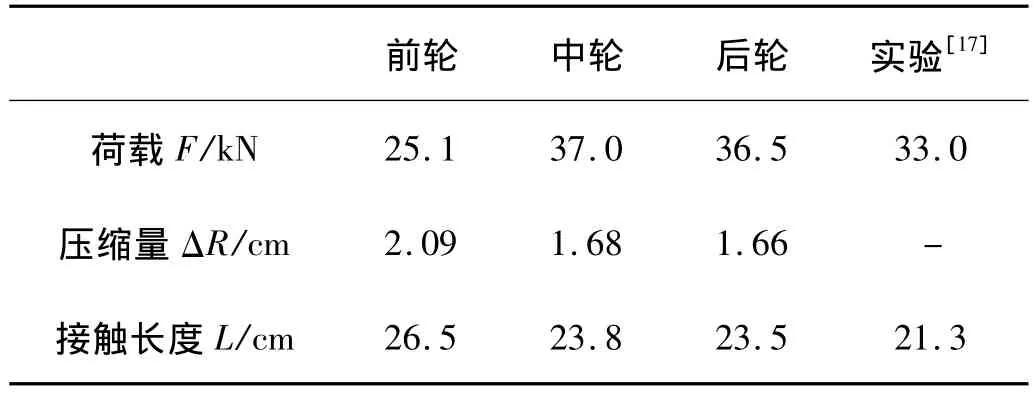
表2 車輪變形與接觸長(zhǎng)度Tab.2 Deformation and contact length of the tire

以前輪為例，動(dòng)荷載計(jì)算結(jié)果見圖8。

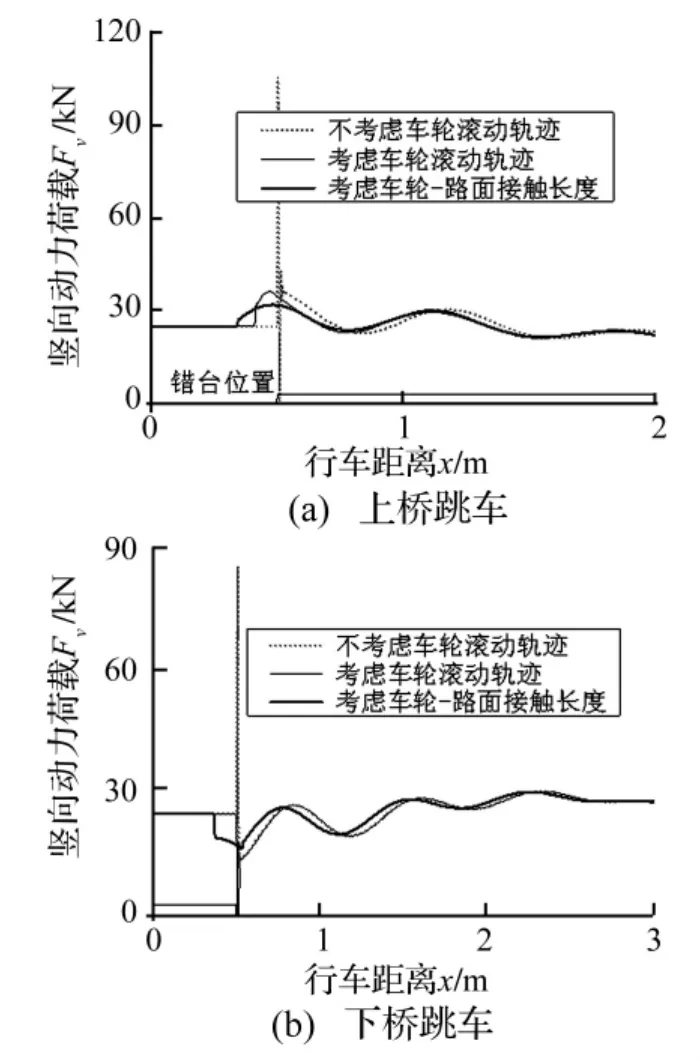
圖8 前輪動(dòng)荷載(h=10 mm，v=30 km/h)Fig.8 Dynamic load of the front tire(h=10 mm，v=30 km/h)

由此可知，若將車輪視為一個(gè)點(diǎn)，上、下橋時(shí)動(dòng)荷載計(jì)算值變化劇烈;采用考慮滾動(dòng)軌跡的圓盤車輪模型后，動(dòng)荷載趨于平緩;考慮車輪-路面接觸長(zhǎng)度后，上橋時(shí)動(dòng)荷載進(jìn)一步減小，下橋時(shí)最大荷載變化不大，但作用位置提前。因此，計(jì)算車輪動(dòng)荷載時(shí)，需考慮輪胎-路面接觸長(zhǎng)度，以準(zhǔn)確反映跳車時(shí)的接觸條件，本文的分析均采用該計(jì)算方法。

考慮車輪滾動(dòng)軌跡與輪胎-路面接觸長(zhǎng)度后，前、中、后輪的動(dòng)力荷載見圖9。由圖可知，車輛上、下橋通過(guò)橋頭錯(cuò)臺(tái)時(shí)，車輪荷載均產(chǎn)生波動(dòng)。因前輪較中、后輪上橋早，故輪力波動(dòng)也較早。

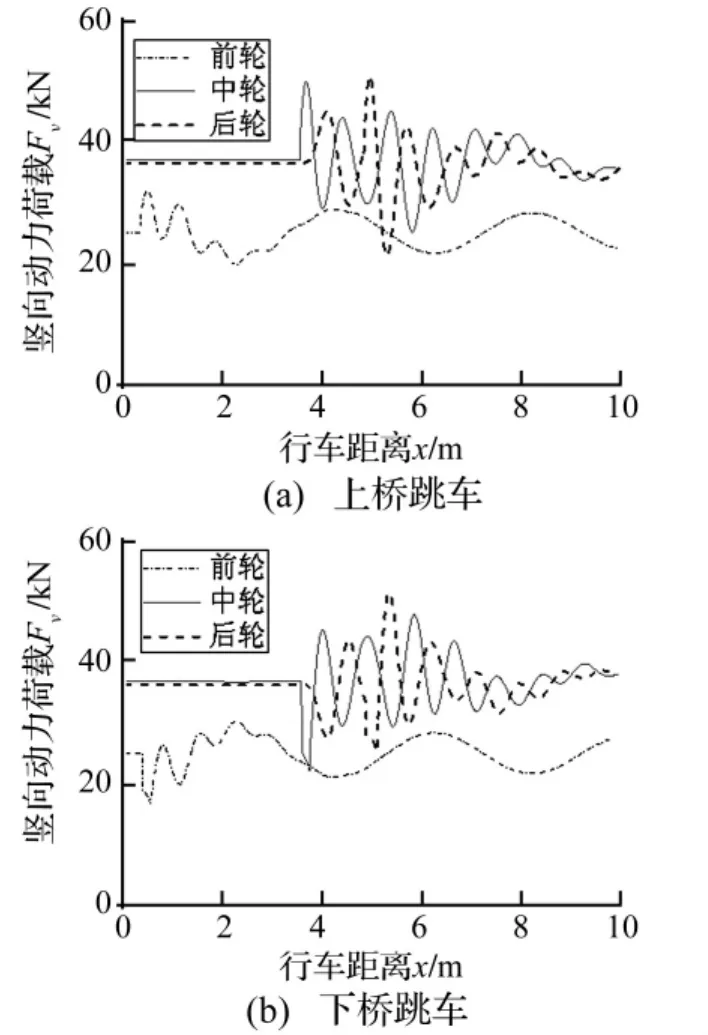
圖9 車輪動(dòng)荷載(h=10 mm，v=30 km/h)Fig.9 Dynamic load of the tire(h=10 mm，v=30 km/h)

用沖擊系數(shù)表示車輪荷載動(dòng)力效應(yīng)為:

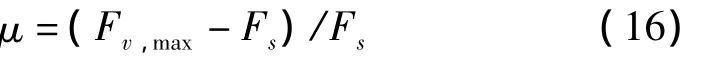
其中:Fs為車輪靜荷載，F(xiàn)v，max為豎向動(dòng)力荷載最大值。圖9的輪載沖擊系數(shù)見表3，上橋的輪載沖擊系數(shù)較下橋大;因上橋最大動(dòng)荷載發(fā)生在車輪剛駛上橋頭錯(cuò)臺(tái)時(shí)，即該動(dòng)荷載作用在橋上局部范圍內(nèi)，本例計(jì)算值略大于文獻(xiàn)［5］規(guī)定的局部加載沖擊系數(shù)(0.3)，小于文獻(xiàn)［6］的局部沖擊系數(shù)(0.75)。

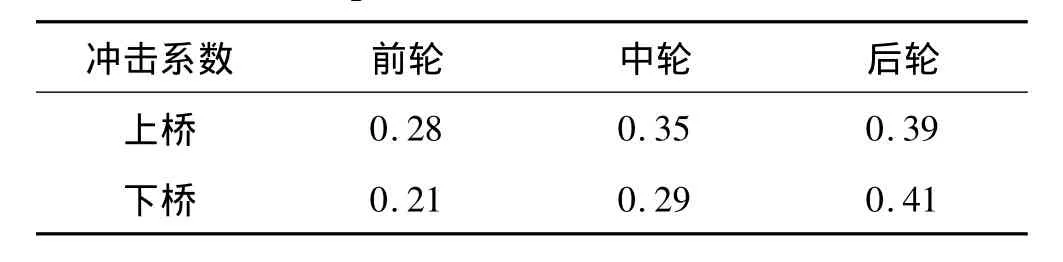
表3 輪載沖擊系數(shù)Tab.3 Impact factor of the load of the tire

圖9(b)中下橋跳車時(shí)輪載有突然減小現(xiàn)象，但仍大于0，說(shuō)明車輪未騰空。據(jù)式(8)、式(14)，得下橋跳車時(shí)的臨界速度見表4。由表4知，考慮輪胎-路面接觸長(zhǎng)度后，臨界速度大大增加。車速大于臨界速度時(shí)，會(huì)產(chǎn)生車輪騰空現(xiàn)象，影響行車穩(wěn)定性及安全性。

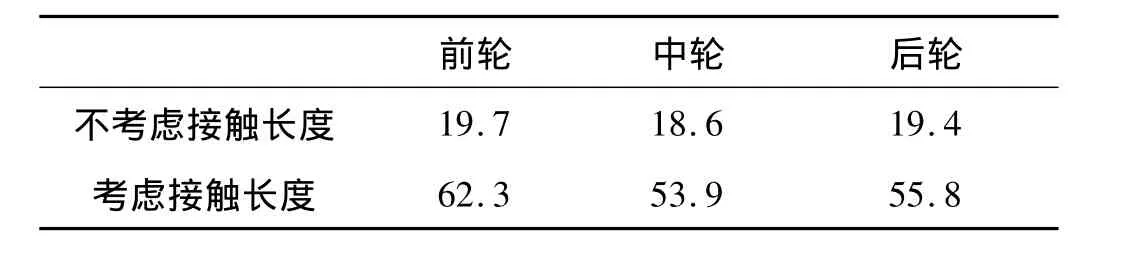
表4 下橋跳車臨界速度vcr(km/h)Tab.4 Critical speed of the tire getting of the bridge

以車速與錯(cuò)臺(tái)高度為例，探討跳車動(dòng)力荷載影響因素。

2.2 車速對(duì)動(dòng)力荷載影響

分別對(duì)上橋、下橋兩種情形，分析車輛以10～80 km/h速度通過(guò)10 mm橋頭錯(cuò)臺(tái)時(shí)的動(dòng)力荷載。

2.2.1 上橋跳車

圖10為上橋時(shí)的車輪荷載。不同車速下最大動(dòng)力荷載均發(fā)生在橋頭錯(cuò)臺(tái)上。

用式(16)求得輪載沖擊系數(shù)，見圖11。

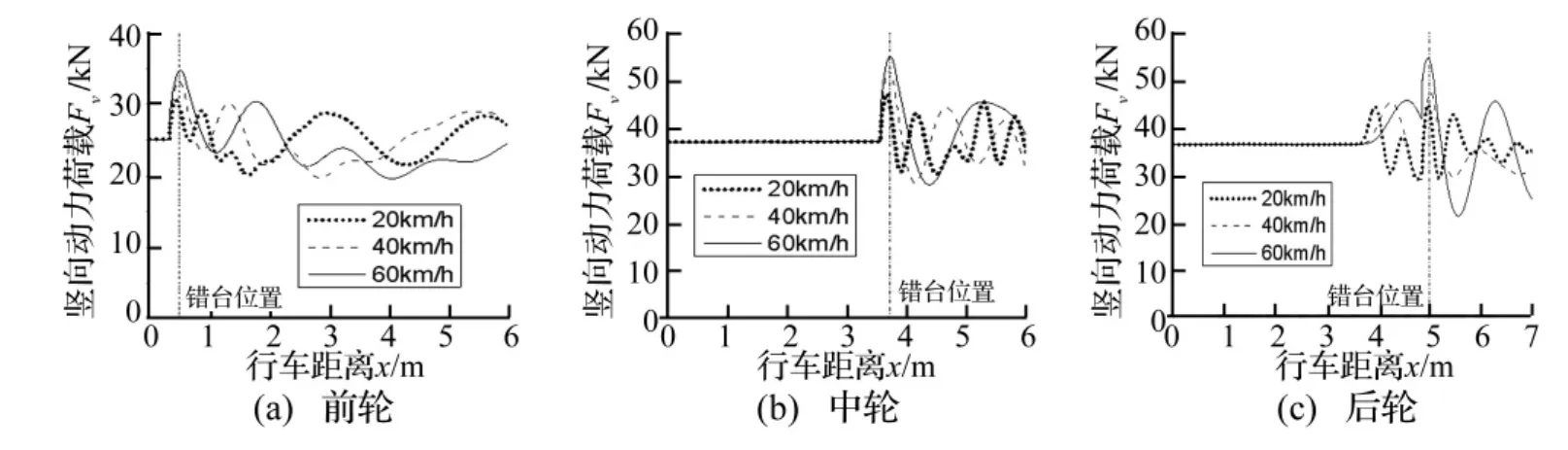
圖10 上橋時(shí)的車輪動(dòng)荷載Fig.10 Dynamic load of the tire getting on the bridge

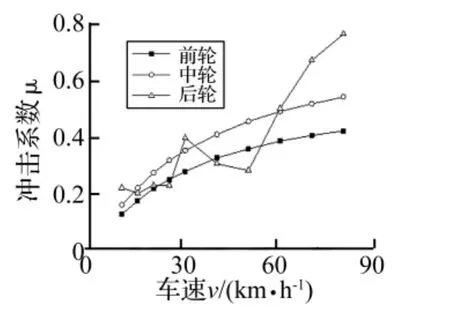
圖11 上橋時(shí)輪載沖擊系數(shù)Fig.11 Impact factor of the tire getting on the bridge

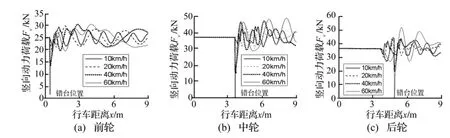
圖12 下橋時(shí)的車輪動(dòng)荷載Fig.12 Dynamic load of the tire getting off the bridge

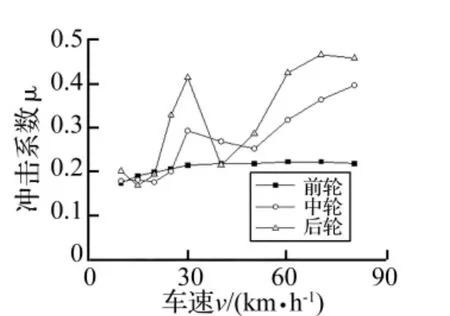
圖13 下橋時(shí)車輪輪載沖擊系數(shù)(h=20 mm)Fig.13 Impact factor of the tire getting off the bridge

前輪、中輪動(dòng)荷載隨著車輛速度的增大而增大，而后輪荷載波動(dòng)較大。產(chǎn)生此現(xiàn)象因?yàn)榍拜啰?dú)立懸掛，中、后輪非獨(dú)立懸掛，故前輪振動(dòng)不影響中、后輪，后輪則受中輪振動(dòng)影響。因此，橋頭沖擊系數(shù)與車輛懸掛系統(tǒng)有關(guān)。圖11中輪載沖擊系數(shù)在0.13～0.76之間。

2.2.2 下橋跳車

圖12為不同速度下橋時(shí)的動(dòng)力荷載。

用沖擊系數(shù)表示動(dòng)荷載效應(yīng)，如圖13所示。前輪沖擊系數(shù)約0.2，隨車速變化很小;中、后輪沖擊系數(shù)隨車速的增加而波動(dòng)，30 km/h和70 km/h車速時(shí)最大，數(shù)值在0.17 ～0.46之間。

由圖12看出，下橋時(shí)最大輪載不一定在錯(cuò)臺(tái)上，離橋頭錯(cuò)臺(tái)距離與車速的關(guān)系如圖14所示。

前輪最大輪載位置到錯(cuò)臺(tái)的距離隨車速的增大而線性增大，80 km/h車速時(shí)距錯(cuò)臺(tái)達(dá)4.7 m;中輪最大輪載位置隨車速的增大而波動(dòng)，70 km/h車速時(shí)距錯(cuò)臺(tái)達(dá)4.0 m;后輪最大輪載作用點(diǎn)離錯(cuò)臺(tái)較近在1 m以內(nèi)。

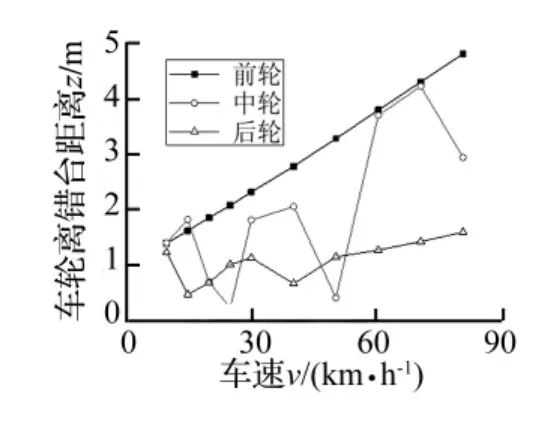
圖14 最大輪載位置與速度關(guān)系Fig.14 The position of the maximum dynamic load of tire

圖15 上橋時(shí)的車輪動(dòng)荷載Fig.15 Dynamic load of the tire getting on the bridge

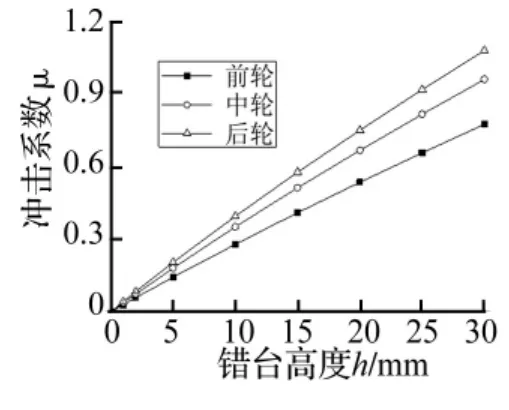
圖16 輪載沖擊系數(shù)與高度關(guān)系Fig.16 The impact factor of dynamic load of the tire

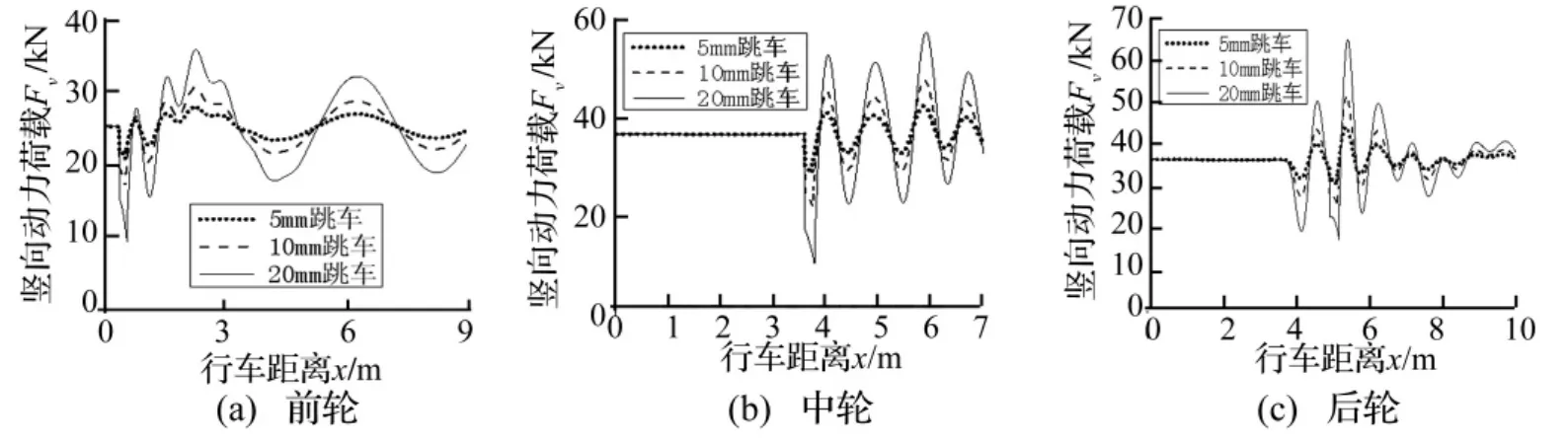
圖17 下橋時(shí)的車輪動(dòng)荷載Fig.17 Dynamic load of the tire getting off the bridge

2.3 跳車高度影響

分析車輛以30 km/h速度通過(guò)1～30 mm高度橋頭錯(cuò)臺(tái)時(shí)的動(dòng)力荷載。

2.3.1 上橋跳車

圖15為不同高度橋頭錯(cuò)臺(tái)導(dǎo)致的車輪動(dòng)力荷載，由此可知，最大輪載均發(fā)生在車輪剛上橋時(shí);錯(cuò)臺(tái)高度越大，動(dòng)力效應(yīng)越明顯。

用沖擊系數(shù)表示動(dòng)力效應(yīng)大小，如圖16所示。沖擊系數(shù)與錯(cuò)臺(tái)高度成正比，后輪沖擊系數(shù)最大，錯(cuò)臺(tái)高度大于10 mm時(shí)超過(guò)0.3，30 mm錯(cuò)臺(tái)的沖擊系數(shù)達(dá)1.08。

2.3.2 下橋跳車

圖17為下橋時(shí)車輪動(dòng)力荷載，由此可知，不同跳車高度下最大輪載的作用位置相同，與橋頭錯(cuò)臺(tái)有一段距離，位置可由圖14確定;錯(cuò)臺(tái)高度越大，動(dòng)力效應(yīng)越明顯。

如圖18所示，輪載沖擊系數(shù)與跳車高度成正比。后輪沖擊系數(shù)最大，錯(cuò)臺(tái)高度超過(guò)10 mm時(shí)中、后輪沖擊系數(shù)超過(guò)0.3，錯(cuò)臺(tái)高度超過(guò)15 mm時(shí)前輪沖擊系數(shù)也超過(guò) 0.3。

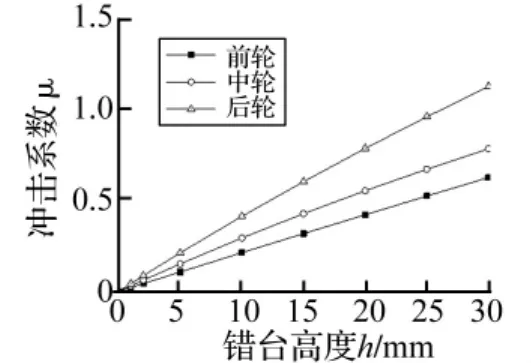
圖18 輪載沖擊系數(shù)與高度關(guān)系Fig.18 The impact factor of dynamic load of the tire

3 結(jié)論

對(duì)橋頭錯(cuò)臺(tái)跳車問(wèn)題，提出考慮輪胎-路面接觸長(zhǎng)度的圓盤車輪模型，結(jié)合基于有限元的車輛動(dòng)力學(xué)分析，計(jì)算橋頭跳車時(shí)的車輪動(dòng)力荷載，可為路、橋設(shè)計(jì)與維護(hù)提供定量參考。實(shí)例分析表明:

(1)采用考慮輪胎與路面接觸長(zhǎng)度的圓盤模型，更符合車輪接觸的實(shí)際情況，所得上橋跳車動(dòng)力荷載明顯降低，下橋跳車的臨界速度則大大增加;

(2)橋頭跳車時(shí)，車輪最大動(dòng)荷載與行車速度關(guān)系與車輪懸掛方式有關(guān)。車輪獨(dú)立懸掛時(shí)，上橋時(shí)車速越大，最大動(dòng)力荷載越大;下橋時(shí)最大動(dòng)力荷載基本與車速無(wú)關(guān)。

(3)橋頭跳車時(shí)的最大動(dòng)力荷載與橋頭錯(cuò)臺(tái)高度成正比;

(4)上橋跳車時(shí)的最大動(dòng)力荷載總位于橋頭錯(cuò)臺(tái)上;下橋跳車時(shí)最大動(dòng)力荷載則離橋頭有一定距離。

(5)橋頭錯(cuò)臺(tái)跳車時(shí)的沖擊系數(shù)會(huì)超過(guò)我國(guó)橋梁規(guī)范中的局部沖擊系數(shù)(0.3)。車輛以30～80 km/h速度上橋通過(guò)10 mm橋頭錯(cuò)臺(tái)時(shí)，輪載沖擊系數(shù)在0.3～0.76之間，下橋跳車時(shí)，10 mm錯(cuò)臺(tái)跳車造成的輪載沖擊系數(shù)在0.17～0.46之間，因此橋頭跳車造成的動(dòng)力輪載不可忽視。

［1］ White D J，Sritharan S，Suleiman M，et al.Identification of the best practices for design，construction，and repair of bridge approaches［R］.Iowa Department of Transportation，Ames.，Jan，2005.

［2］張麗芳，艾 軍.橋頭引道沉降對(duì)簡(jiǎn)支梁沖擊效應(yīng)的影響分析［J］.振動(dòng)與沖擊，2009，28(10):4-7.

ZHANG Li-fang，AI Jun. Impact influence of a bridge approach differential settlement on a simply supported bridge［J］.Journal of Vvibration and Shock，2009，28(10):4-7.

［3］ Roy S，Thiagarajan G.Nonlinear finite-element analysis of reinforced concrete bridge approach slab［J］.Journal of Bridge Engineering，2007，12(6):801-806.

［4］Liu H L，Ng C，F(xiàn)ei K.Performance of a geogrid-reinforced and pile-supported highway embankment over soft clay:case study［J］.Journal of Geotechnical and Geoenvironmental Engineering，2007，133(12):1483-1493.

［5］JTJ D60-2004，公路橋涵設(shè)計(jì)通用規(guī)范［S］.

［6］American association of state highway and transportation officials(AASHTO)［S］.LRFD Bridge Design Specification and Commentary，Washington D.C.，2004.

［7］許士強(qiáng)，陳水生，桂水榮.公路橋梁汽車沖擊系數(shù)對(duì)比研究［J］.工程建設(shè)與設(shè)計(jì)，2006(12):73-75.

XU Shi-qiang，CHEN Shui-sheng，GUI Shui-rong.The study of the comparison for impact coefficient caused by vehicle for highway bridges［J］.Construction ＆ Design for Project，2006(12):73-75.

［8］張洪亮，胡長(zhǎng)順.基于五自由度車輛模型的橋頭搭板容許縱坡變化值研究［J］.土木工程學(xué)報(bào)，2005，38(6):125-131.

ZHANG Hong-liang， HU Chang-shun. A study on the allowable differential slope of the approach slab with fivedegree-freedom vehicle model［J］.China Civil Engineering Journal，2005，38(6):125-131.

［9］Shi X M，Cai C S，Chen S R.Vehicle induced dynamic behavior of short-span slab bridge considering effect of approach slab condition［J］.Journal of Bridge Engineering，2008，13(1):83-92.

［10］ Cheli F，Braghin F，Brusarosco M，et al.Design and testing of an innovative measurement device for tyre road contact forces［J］.Mechanical Systems and Signal Processing，2011，25(6):1956-1972.

［11］ Potter T E C，Cebon D，Collop A C，et al.Road-damaging potential of measured dynamic tyre forces in mixed traffic［J］.Journal of Automobile Engineering，1996，210(3):215-226.

［12］劉曉明，趙明華，黎大志.基于整車模型的橋頭路面動(dòng)力荷載分析［J］.公路交通科技，2007，24(7):39-43.

LIU Xiao-ming，ZHAO Ming-hua，LI Da-zhi.Analysis of dynamic force on the bridge approaches pavement based on whole vehicle model［J］.Journal of Highway and Transportation Research and Development，2007，24(7):39-43.

［13］Ding L，Hao H，Zhu X.Evaluation of dynamic vehicle axle loads on bridges with different surface conditions［J］.Journal of Sound and Vibration，2009，323(3-5):826-847.

［14］丁 勇，謝 旭，黃劍源.考慮車輪滾動(dòng)軌跡的橋頭跳車動(dòng)力荷載計(jì)算方法及影響因素分析［J］.工程力學(xué)，2013，30(2):135-142，149.

DING Yong，XIE Xu，HUANG Jian-yuan.A numerical method foranalyzingthe dynamic load in bridge-head bumping considering the rolling trace of wheel and the analysis of influencing factors［J］.Engineering Mechanics，2013，30(2):135-142，149.

［15］丁 勇，布占宇，謝 旭，等.考慮橋面板振動(dòng)的橋梁結(jié)構(gòu)低頻噪聲分析［J］.土木建筑與環(huán)境工程，2011，33(2):58-64，69.

DING Yong，BU Zhan-yu，XIE Xu，et al.Analysis of lowfrequency noise of bridge considering the vibration of bridge deck［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2011，33(2):58-64，69.

［16］ Task committee on bridge vibration.jsce，measurement and evaluation of bridges vibration［M］.Tokyo:Gihodo Shuppan Co.Ltd.1993.

［17］謝水友.輪胎接觸壓力對(duì)瀝青路面結(jié)構(gòu)的影響研究［D］.西安:長(zhǎng)安大學(xué)，2003.