機器人運動功能位姿矩陣研究與應用

韓 雪

（1.遼寧工程職業學院，遼寧 沈陽 110136；2.鐵嶺技師學院，遼寧 鐵嶺 112006）

1 概述

工業機器人末端執行器的動作是通過各關節的運動傳遞來實現的，各個關節的運動直接決定了其末端執行器最終能實現的動作、功能，因此機器人運動功能位姿描述對于機器人運動功能設計有十分重要的意義。機器人的運動功能位姿描述一般是通過運動功能位姿矩陣來表述的，本文詳細論述了機器人運動功能位姿矩陣的構成及應用。

2 運動功能位姿矩陣的構成

運動功能位姿矩陣用于表示機器人末端執行器在整個機器人中相對機座的位置和姿態變化。它由幾何齊次坐標變換矩陣和運動齊次坐標變換矩陣構成。

2.1 幾何齊次坐標變換矩陣

幾何齊次坐標變換矩陣用于描述機器人從機座坐標系變換到末端執行器坐標系所經歷的一系列坐標變換。其中，繞X軸旋轉的旋轉變換矩陣是：

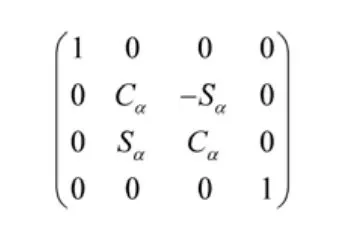
繞Y軸旋轉的旋轉變換矩陣是：

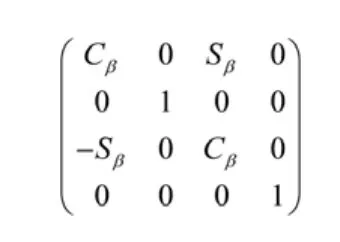
繞Z軸旋轉的旋轉變換矩陣是：

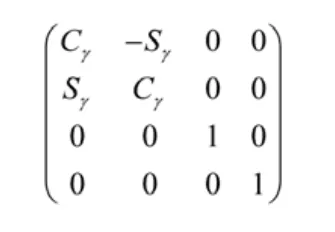
沿X軸移動的移動變換矩陣是：

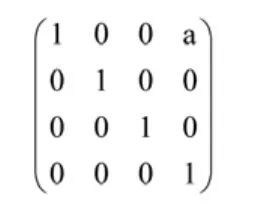
沿Y軸移動的移動變換矩陣是：

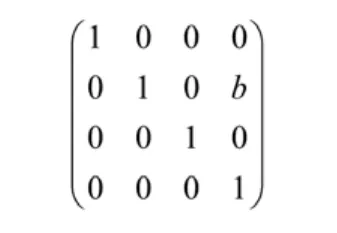
沿Z軸移動的移動變換矩陣是：

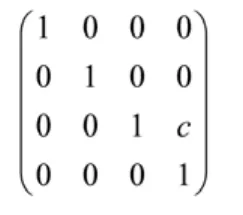
2.2 運動齊次坐標變換矩陣

運動齊次坐標變換矩陣用于描述幾何齊次坐標變換后關節的姿態，如繞Z軸轉動的回轉關節矩陣是：

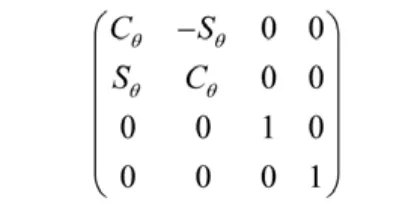
繞Z軸移動的移動關節矩陣是：

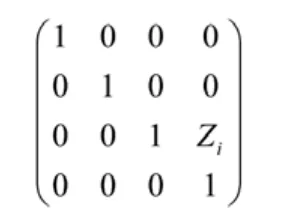
3 應用舉例

如圖所示機器人結構簡圖（見圖1）。

3.1 圖紙分析

該機器人共包括三個自由度，依次為關節1的回轉運動，關節2 的回轉運動，關節3 的直線運動。

3.2 幾何齊次坐標變換分析

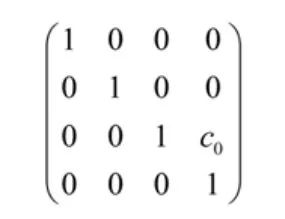
從機座坐標系X0-Z0 變換為關節1的坐標系X1-Z1需沿Z 軸移動c0距離，幾何齊次坐標變換矩陣為：

從關節1坐標系X1-Z1變換為關節2的坐標系X2-Y2需繞X軸轉動90°并沿Z軸移動c1，幾何齊次坐標變換矩陣為：

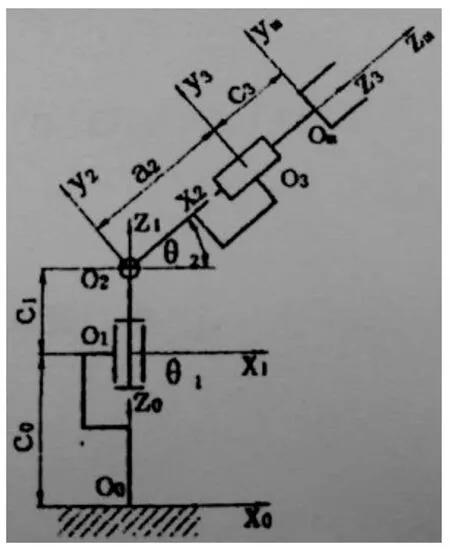
圖1 機器人結構簡圖

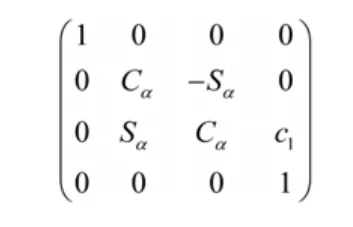
從關節2坐標系X2-Y2變換為關節3的坐標系Y3-Z3需繞Y軸旋轉90°并沿X軸移動2a距離，幾何齊次坐標變換矩陣為：

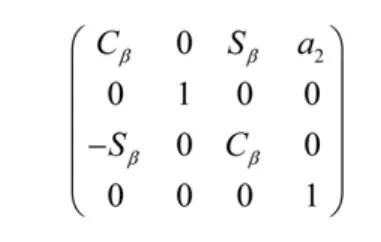
從關節3坐標系Y3-Z3變換為末端執行器坐標系Ym-Zm需沿Z軸移動3c距離，幾何齊次坐標變換矩陣為：

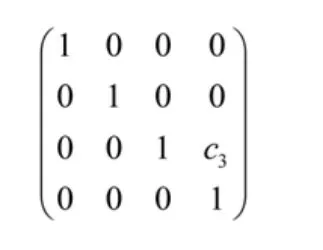
3.3 運動齊次坐標變換分析

關節1作繞Z軸旋轉的回轉運動，運動齊次坐標變換矩陣為：

關節2作繞Z軸旋轉的回轉運動，運動齊次坐標變換矩陣為：

關節3作沿Z軸移動的直線運動，運動齊次坐標變換矩陣為：

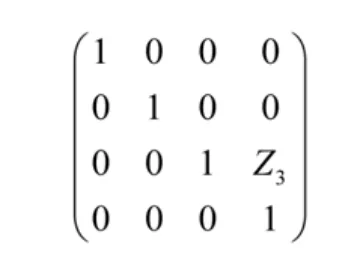
3.4 列出運動功能位姿矩陣

其中：

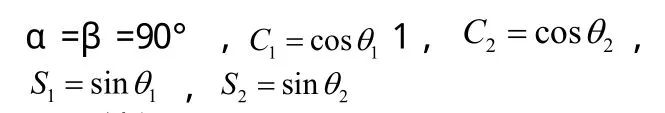
結語

通過觀察運動功能位姿矩陣，可以清楚的了解機器人自由度個數，各關節運動性質及排列順序，在基準狀態時關節軸的方位等等。

[1]關慧貞，馮辛安.機械制造裝備設計（第3版）[M].北京：機械工業出版社，2012.