平衡損失函數下具有時間變化效應的信度保費

李新鵬，吳黎軍

(新疆大學數學與系統科學學院，烏魯木齊 830046)

1 預備知識

在保險實際應用中，精算師的一個重要任務之一就是對給定的風險制定一個合適的保費。現代信度理論起源于Bühlmann［1］得到了任意分布下的凈保費信度估計。信度理論是基于過去的索賠經歷來制定保費的一種定量方法。信度保費為樣本均值和聚合保費的加權和，其中權重因子又被稱為信度因子。

令Xi表示保單持有人在第i個保單時期的索賠額，Xi的分布依賴于風險參數Θ。由于風險的非其次性，一般假設Θ是隨機變量，具有先驗分布為 π(θ)，若給定 Θ =θ，Xi(i=1，2…n)相互獨立，且有相同的分布函數F(x，θ)。信度理論的目的是在給定保單持有人的前n個時期根據索賠經歷來計算第n+1個時期的保費。如果將估計限定在索賠額的線性函數中，則得到著名的信度公式:

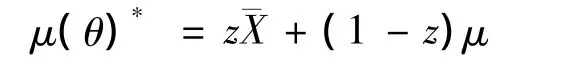
其中:z=n/(n+k)為信度因子;k為條件方差的期望值與條件期望的方差值的比值;為樣本均值;μ為聚合保費。

經典的信度理論中假定不同年份的索賠序列有共同的風險參數，在風險參數給定時，各年的索賠相互獨立，且具有相同的分布，沒有考慮不同年份之間風險的時間效應。溫利民等［2］在均方損失函數下研究了各年索賠風險間具有時間變化效應的信度模型，得到了相應的信度保費。考慮時間方面相依性的信度模型與實際情況更為符合。溫利民等在2009年研究了各年索賠風險間具有等相關的信度模型，得到了相應的信度保費。Bolancé等［3］建立了索賠頻率風險模型，得到了時間效應為自相關時間序列時的信度保費。Purcaru與Denuit［4］在 Poisson索賠頻率風險模型中討論了相依結構對信度估計的影響。Frees等［5］研究了時間效應為Student-t copula時的信度保費。

經典的決策論中，損失函數的選擇通常取決于估計的精確性，然而，擬合的好壞也是一個重要的標準。Zellner［6］引入了平衡損失函數的概念，它既反映了好的擬合度又反映了估計的精確性，函數如下:

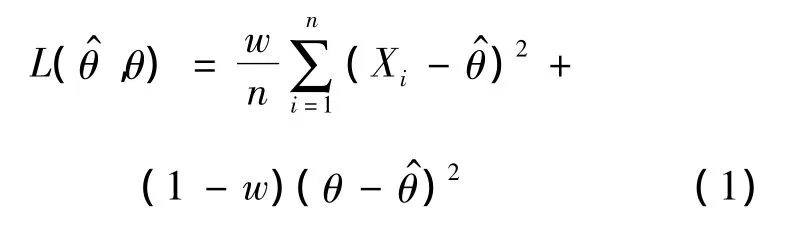
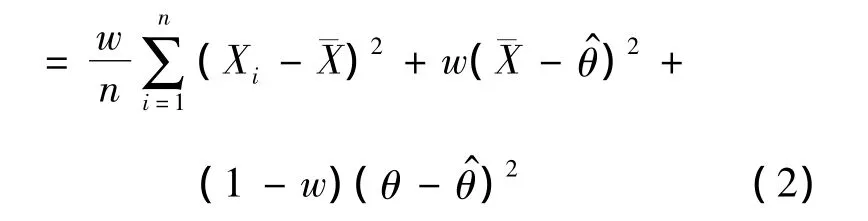
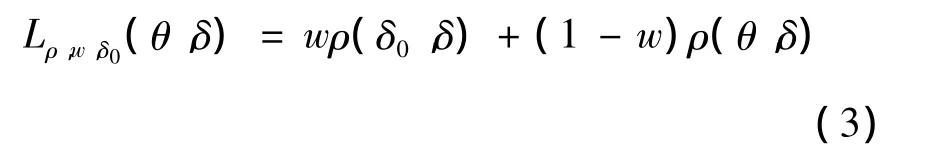
其中:ρ為距離函數;δ0為目標估計，它通常由極大似然估計、最小二乘法或者無偏性條件獲得;δ為θ的估計值;距離函數通常選為均方誤差損失函數。

本文在平衡損失函數下考慮了具有時間變化效應的信度模型，并且得到了相應的信度保費［7-10］。

2 模型假設與準備

在信度理論中，假設保單組合的風險參數為Θ，且有n年的索賠額，由于風險的非齊次性，風險參數Θ假定為隨機變量。本文的目標為預測保單在未來1年的索賠Xn+1。但與經典的信度理論不同，本文假設在風險參數給定的條件下，索賠隨機變量 X1，X2，…，Xn有各自的風險參數 Θ1，Θ2，…，Θn，且這些風險參數具有某種相依結構。模型的基本假設如下:

假設1 給定時間變化效應Θi=θi時，索賠額 Xi，i=1，…，n 互相獨立且同分布 E(Xi|Θi)=μ(Θi)，Var(Xi|Θi)=σ2(Θi)，i=1，2，…，n。

假設2 風險參數Θi的分布函數為πi(θ)，且 E［μ(Θi)］=μ，E［σ2(Θi)］=和協方差Cov［μ(Θi)，μ(Θj)］= τiτj.i，j=1，…n。

假設3 本文中平衡損失函數為:

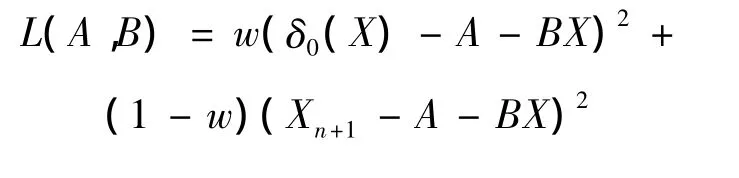
其中 δ0(X)為目標估計，X=(X1，…，Xn)'且E［δ0(X)］= μδ，Cov［δ0(X)，Xi］=di，i=1，2，…，n，w為權重因子。

本文目標為求解下面最優化問題:

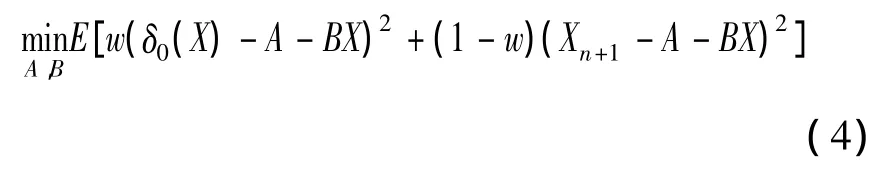
為求解最優化問題(4)，記L(X，1)={a0+

引理1～3［2］表明了相依結構的一些簡單但重要的性質。

引理1 在假設1和假設2下，有:

①Xi的均值為

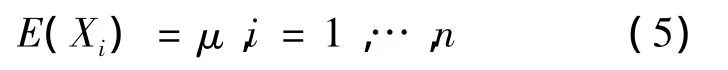
②過去索賠和未來索賠的協方差為

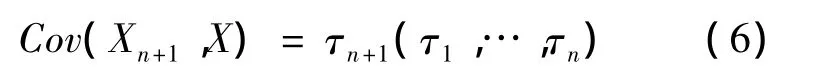
③X的協方差矩陣為

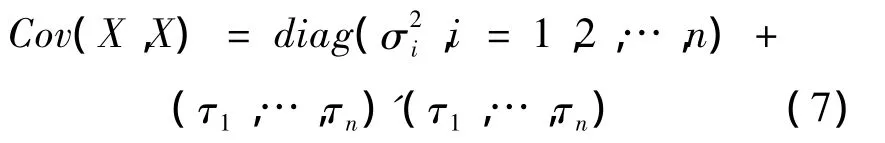
其中diag［…］為對角矩陣。

④X的協方差矩陣的逆為

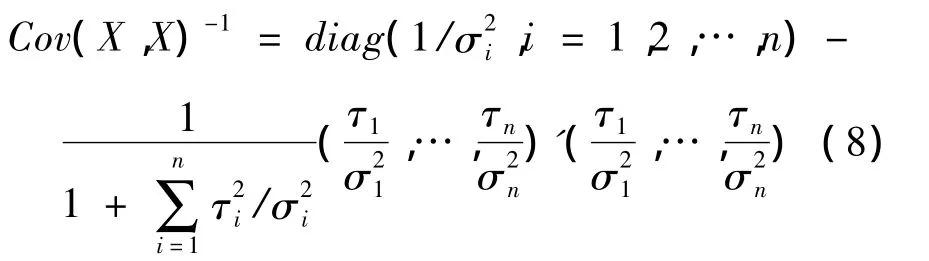
引理2 假設(X'1×p，Y'1×q)'為一隨機向量，期望和協方差矩陣分別為(μ'X，μ'Y)和則當時，期望損失E(Y-A-BX)'(Y-A-BX)達到最小。

引理3 風險Xn+1的非齊次信度估計為Xn+1在L(X，1)上的正交投影，即

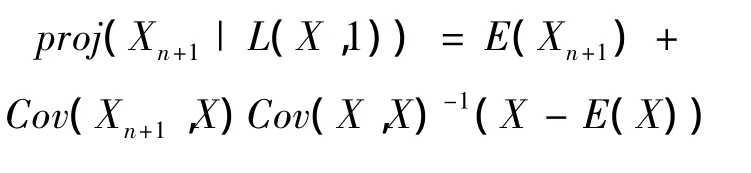
3 平衡損失函數下的信度估計

定理1為最優化問題(4)的解，即未來索賠Xn+1的信度保費。

定理1 在假設1～3下，運用平衡損失函數，Xn+1的最優線性非齊次估計為

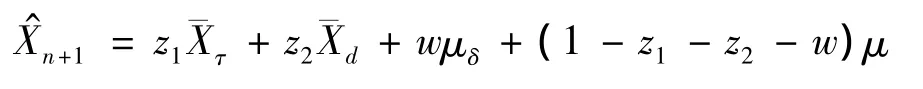
其中:

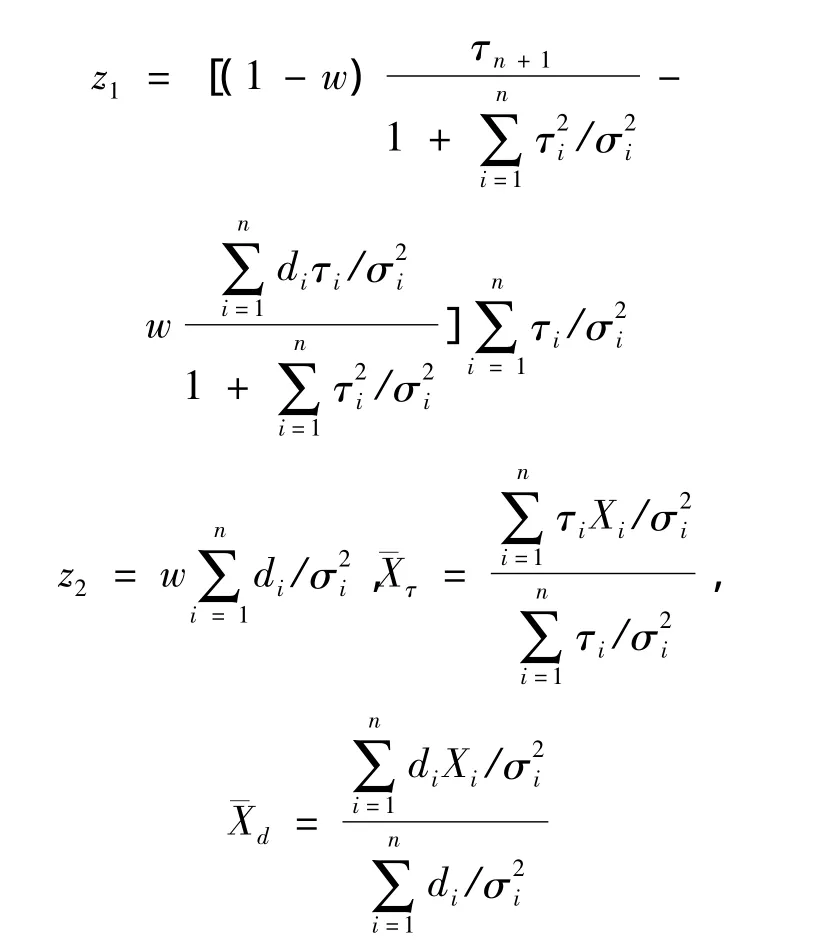
證明引入一隨機變量Y=Iδ0(X)+(1-I)Xn+1，其中I為0-1隨機變量，它獨立于其他的隨機變量，并且P(I=1)=1-P(I=0)=w，w為式(4)中的權重因子。因此，最優化問題(4)等價于

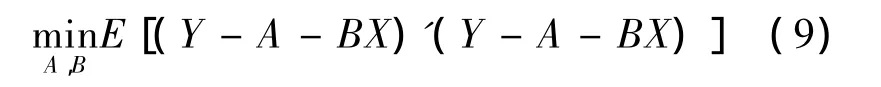
由引理2和引理3知，下一年保費的最優估計為

根據Y的定義，均值μY為:

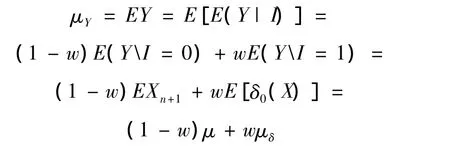
又因為E(XI)=E(X)為一常數，所以

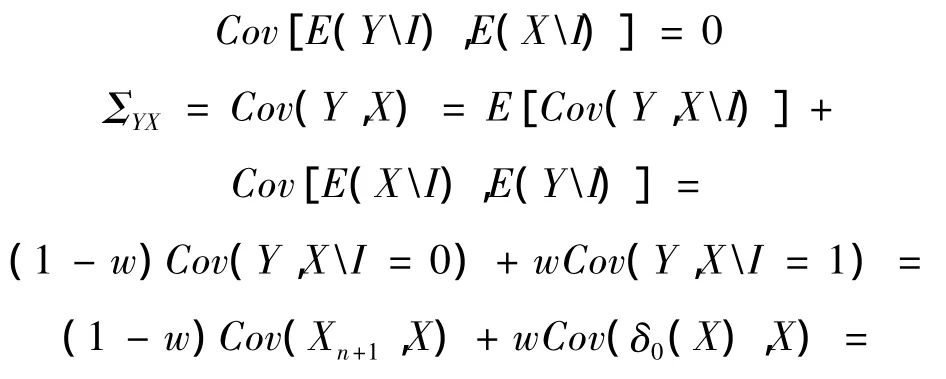
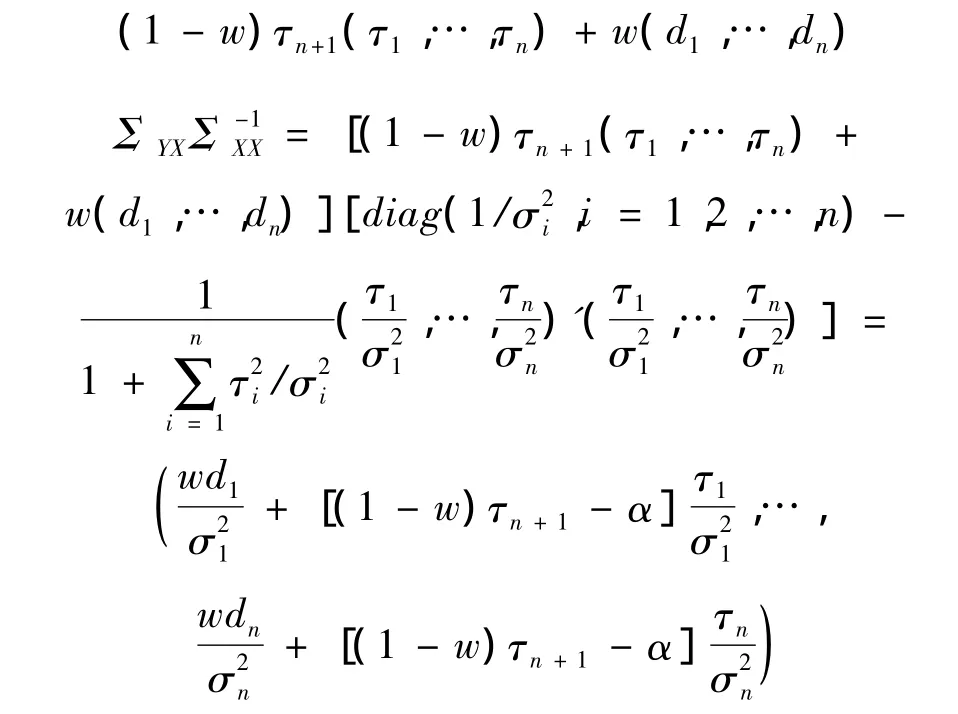
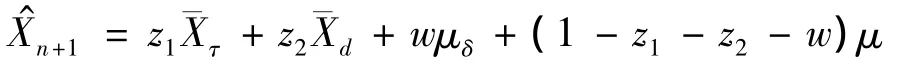
定理得證。

注1 當w=0時，此定理給出的保費與溫利民等在2012年提出的具有時間變化效應信度模型的保費一致。

4 Bühlmann-Straub模型的信度估計

本節將給出在平衡損失函數下具有時間變化效應的Bühlmann-Straub信度模型的保費。將假設1中的Var(Xi|Θi)=σ2(Θi)改為 Var(Xi|Θi)=σ2(Θi)/mi，i=1，2，…，n，mi為 Xi自然權重因子，其他假設不變。

引理4 在本文第3節的假設和上面的假設下，有以下結果:

①Xi的均值為

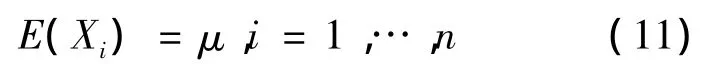
②過去索賠和未來索賠的協方差為

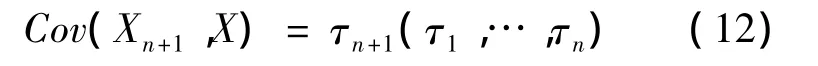
③X的協方差矩陣為

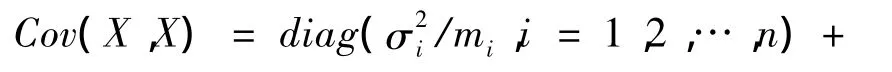
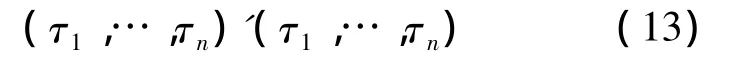
其中diag［…］為對角矩陣。

④X的協方差矩陣的逆為

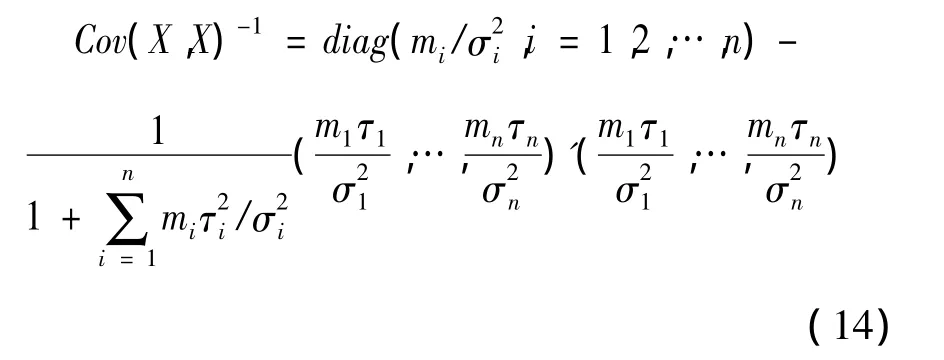
定理2 在本文第3節假設和本節假設下，運用平衡損失函數，Xn+1的最優線性非齊次估計為

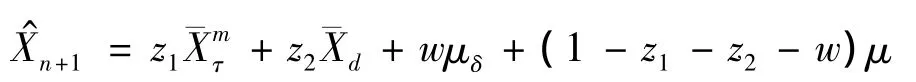
其中:

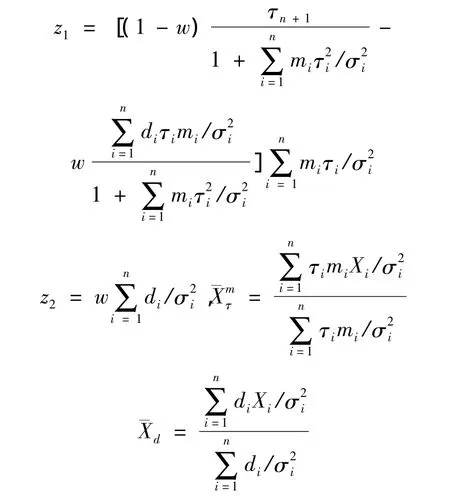
定理2的證明與定理1的證明類似，所以只給出粗略的證明。

證明引入一隨機變量Y=Iδ0(X)+(1-I)·Xn+1，其中I為0～1隨機變量，它獨立于其他的隨機變量，并且P(I=1)=1-P(I=0)=w，w為式(4)中的權重因子。因此，最優化問題(4)等價于

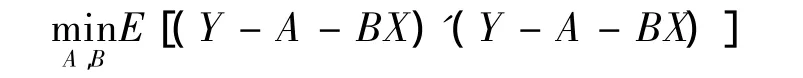
由引理2和引理3知:下一年保費的最優估計為

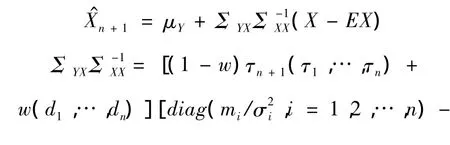
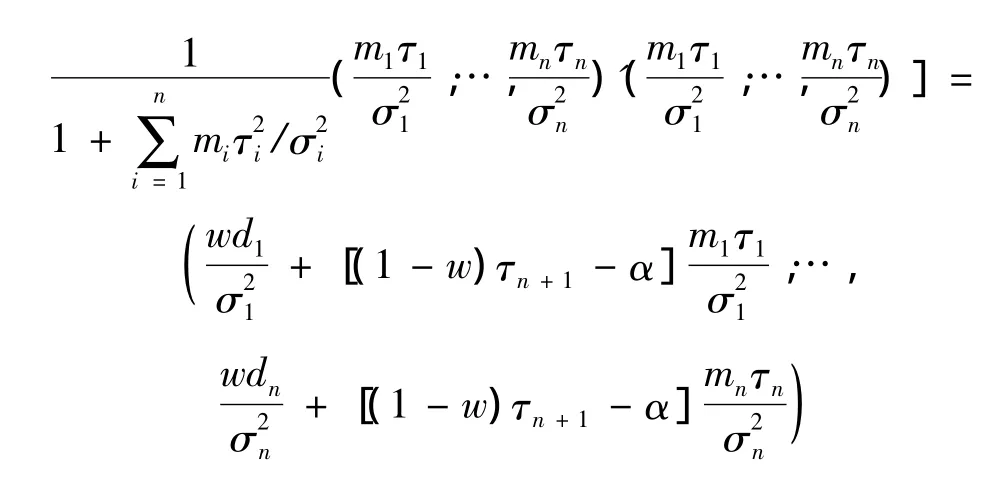
其中

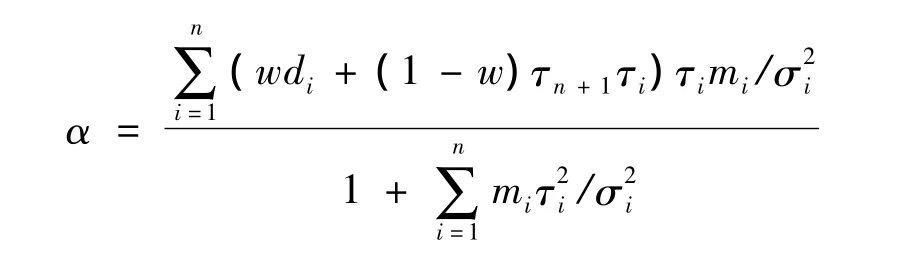
所以，下一年最優非齊次信度保費為

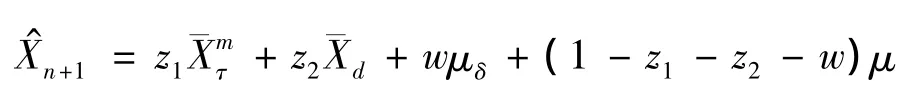
5 結束語

本文運用平衡損失函數，研究了具有時間變化效應的Bühlmann和Bühlmann-Straub信度模型的保費估計問題，并且推導出相應的信度保費，但是對于參數的估計還需今后深入研究。

［1］Bühlmann H，Gisler A.A course in credibility theory and its applications［M］.Netherlands：Springer，2005：77-264.

［2］溫利民，鄭丹，章溢.具有時間變化效應的信度模型［J］.江西師范大學學報：自然科學版，2012，36(3)：249-252.

［3］Bolancé C，Guillé M，Pinquet J.Time-varying credibility for frequency risk models：estimation and tests for autogressive specification on the random effects［J］.Insurance：Mathematics and Economics，2003，33(2)：273-282.

［4］Purcaru O，Denuit M.On the dependence induced by frequency credibility models［J］.Belgian Acturial Bulletin，2002，2(1)：73-79.

［5］Frees E W，Wang Ping.Credibility using copulas［J］.North American Acturial Journal，2005，9(2)：31-48.

［6］Zellner A.Bayesian and non-Bayesian estimation using balanced loss functions［M］.New York：Springer-Verlag，1994：377-390.

［7］Wen Limin，Wu Xianyi，Zhou Xian.The credibility premiums for models with dependence induced by common effects［J］.Insurance：Mathematics and Economics，2009，44(1)：19-25.

［8］Wu Xianyi，Huang Weizhong.The credibility premiums with common effects obtained under balanced loss functions［J］.Chinese Journal of Applied Probability and Statistics，2012，28(2)：203-216.

［9］Wen Limin，Wang Wei，Yu Xueli.Credibility models with error uniform dependence［J］.Journal of East China Normal University：Natural Science，2009，5：118-126.

［10］Gómez-Deniz E.A generalization of the credibility theory obtained by using the weighted balanced loss function［J］.Insurance：Mathematics and Economics，2008，42：850-854.