高壓直流輸電系統的反饋線性化控制器設計及仿真

朱紅萍，李白雅，李 燕

(湖南科技大學信息與電氣工程學院，湖南湘潭411201)

高壓直流輸電(HVDC)在運行過程中會受到或小或大的擾動，如交流系統發生單相或三相短路故障，直流輸電線出現短路故障，使系統的正常運行出現不穩定，直流輸電系統的基本穩態調節特性為:整流側由定電流特性和定α0特性，逆變側由定 δ0特性和定電流特性組成［1-2］。HVDC系統內在的非線性使控制器的設計成為難點，整流側和逆變側的觸發角對直流電流的變化率很敏感，當故障被清除時將導致直流電流和電壓的振蕩，這種振蕩將會損壞換流閥［3-4］。本文提出一種簡單的反饋線性化方法設計控制器，得到換流閥的觸發角，用PSCAD/EMTDC軟件仿真了在交流系統發生故障和受端是弱交流系統時的直流電流變化情況，結果表明了該控制器優于常規的PI控制器。

一 HVDC系統模型

一個兩極的6脈動換流器組成的HVDC系統如圖1所示。

由圖1得到直流電流Id的表達式為

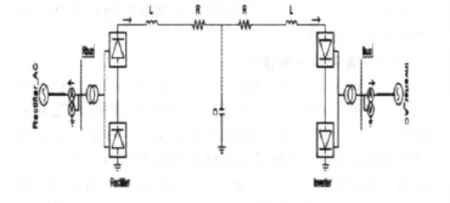
圖1 直流輸電系統模型

式中:LdΣ表示直流輸電線路的等值電感和，RdΣ表示直流輸電線路的等值電阻和，Vdor表示整流器的理想空載直流電壓，Vdoi表示逆變器的理想空載直流電壓，α表示整流器的觸發滯后角，β表示逆變器的觸發越前角。如果將式(1)進行變換:，則可以用下式表示直流電流方程:

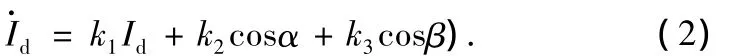
可以把系統看成是偽線性的，反饋線性化控制器為

對于HVDC系統，α的計算可以表示如下:

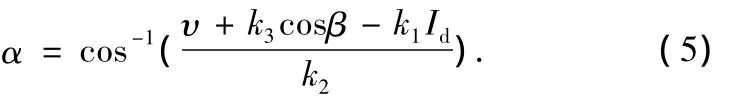
令系統的跟蹤誤差e=Idref-Id，Idref為電流參考值，為了保持Id為常數，跟蹤誤差e用PID調節器調節，用下式表示為

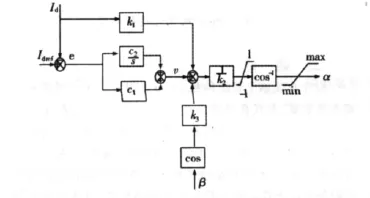
圖2 整流器的α控制器

c1，c2的取值都是大于0的數，可以根據PI的經驗取值，k1，k2，k3的值用 BP 算法來估算。cosα，cosβ，Id作為神經元的輸入，k1，k2，k3作為神經元的網絡權值，是神經元的輸出［5］。其模型用圖3表示。

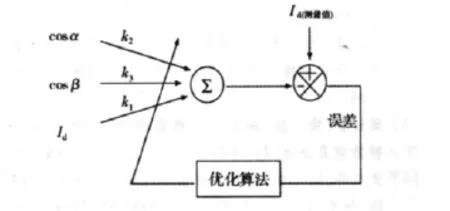
圖3 神經網絡模型

為了訓練神經網絡，直流輸電系統采用常規的PI控制器，得到的測量值，β從逆變器測量得到。

二 算例仿真

為驗證本文的反饋線性化控制器的優越性，在PSCAD/EMTDC的HVDC實例中進行了仿真分析，直流系統采用GIGRE HVDC BENCH MARK MODEL，將本文的反饋線性化控制器作為整流器的控制器，逆變側的β控制器，γ控制器采用原系統的控制器，對系統的運行進行了仿真。系統整流側參數:變壓器為500 kV，1 000 MW，采用12脈波整流，線電壓為 345 kV，SCR=2.5@84.0deg，直流電壓為0.89PU;逆變側的參數:變壓器為500 kV，1 000 MW，采用12脈波整流，線電壓為 230 kV，SCR=2.5@75.0 deg。整流器的 α 控制器的參數:c1=70，c2=1，k1，k2，k3的值由神經網絡優化決定。αmin=0.087 3 rad，αmax=2.7 rad。逆變側的β控制器，γ控制器采用HVDC實例中的參數。圖4對整流側交流母線發生單相接地故障進行了仿真(在0.3 s發生故障，持續0.05 s)，圖5對整流側交流母線發生單相接地故障進行了仿真(在0.3 s發生故障，持續0.05 s)，圖6對逆變側交流母線發生單相接地故障并同時改變SCR進行了仿真(在0.3 s發生故障，持續0.05 s)，圖7對逆變側發生直流短路故障進行了仿真(在0.3 s發生故障，持續0.05 s)，圖8是采用BP時的適應值收斂曲線。

圖4 在兩種控制器下逆變側發生單相短路時的直流電流波形對比

圖5 在兩種控制器下整流側發生單相短路時的直流電流波形對比

圖6 改變SCR的逆變側單相短路時直流電流在兩種情況下的波形

圖7 逆變側直流短路故障時直流電流在兩種情況下的波形

從圖4可以得出，常規的PI控制電流波形出現多峰，振蕩時間長。采用本文提出的反饋線性化控制方法，能使振蕩時間縮短。從圖5可以得出，采用反饋線性化控制方法能使振蕩減少，穩定時間縮短。圖6采用常規的PI控制，出現超調大，多峰的現象，反饋線性化控制方法改善了這種缺點。圖7反映了改變逆變側的SCR，常規的PI控制，系統更易發生振蕩。

圖8 fitness的變化過程曲線

三 結語

對于直流輸電系統的穩定運行，設計一個合適的控制器非常重要，尤其在系統發生故障時，如何快速穩定直流電流。本文提出的反饋線性控制器對整流器觸發角的控制，在一個非線性系統中消除了非線性，使其成為一個偽線性的系統，具有線性系統的形式。PI控制器和反饋線性化控制應用于直流輸電系統發生短路故障，直流電流的變化情況運用PSCAD/EMTDC進行了仿真，可以得出結論:反饋線性化控制器使直流電流的振蕩減少，恢復時間縮短，系統的魯棒性更好。

［1］戴熙杰.直流輸電基礎［M］.北京:水利電力出版社，1990.

［2］張躍鋒，顏 偉，朱蕾蕾.交直流混合輸電系統的換流變壓器分接頭控制［J］.中國電力，2008，41(4):20-24.

［3］周長春，徐 政.聯于弱交流系統的HVDC故障恢復特性仿真分析［J］.電網技術，2003，27(11):18-21.

［4］黃志嶺，田 杰.基于詳細直流控制系統模型的EMTDC 仿真［J］.電力系統自動化，2008，32(2):45-48.

［5］張德豐.Matlab神經網絡應用設計［M］.北京:機械工業出版社，2009.

［6］周孝法，陳 陳，宋正強，等.基于改進 PSO算法的HVDC PI控制器優化設計［J］.高電壓技術，2009，35(2):408-413.

［7］胡 江，魏 星.基于自適應粒子群算法的直流輸電PI控制器參數優化［J］.電網技術，2008，32(2):71-74.