四個熱力學基本關系式和Maxwell公式的理解與記憶①
崔洪友,周子彥,禚淑萍
(山東理工大學化工學院,山東淄博255049)
在學習化工熱力學的過程中,學生經常感到一些關系式難以記憶。雖然這些關系有些已經在物理化學中學過,但學生經常反映還是容易混淆。準確理解這些關系式中所涉及各種函數的基本概念及其推導過程是學好化工熱力學的根本,但學會一些巧妙的記憶方法還是會起到事半功倍的效果。文獻中也曾有過關于這些關系式的報道[1-4],但記憶起來仍然不是很方便。這里僅就自己多年來講授化工熱力學課程所總結出來的一點記憶技巧和體會與大家分享。
一 封閉體系的四個熱力學基本關系
封閉體系的四個熱力學基本關系是:

(一)推導與準確理解
這四個熱力學基本關系式實質上是熱力學第一定律和熱力學第二定律在均相封閉中實用的一種數學表達。對于封閉體系,體系與環境沒有物質交換,只有能量交換。不論是否為均相體系,體系內能的增加只是從環境得到的功和熱之和,故由熱力學第一定律總有

根據熱力學第二定律,體系與環境交換的功和熱必須滿足

當系統與環境只有體積功交換時,

將式(6)和式(7)代入式(5),得到式

再根據熱焓H、Gibbs自由能G和Helmholtz自由能A的定義式
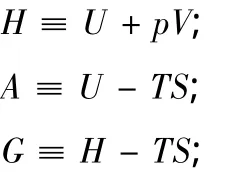
并分別取其全微分得到
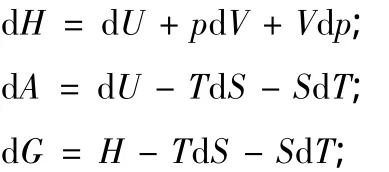
將式(8)代入上3式得出


由推導過程中的假設知,式(8)~式(11)的適應條件為只有體積功的封閉體系。
式中所有的物理量均為狀態函數,當體系達到完全平衡狀態時,其值已確定,此時狀態函數的變化值與過程無關。故不論變化過程是否可逆,式(8)~式(11)均取等號,得到式(1)~式(4)。
所謂完全平衡即達到熱平衡、力平衡、化學勢平衡。換句話說,即體系中各處不僅達到了溫度和壓力不再隨時間發生變化,而且體系的組成也不再隨時間發生變化。在教科書中通常會看到式(1)~式(4)的適用條件為:只有體積功且無化學反應的均相封閉體系。那么這里為什么要加上一個無化學反應的限制條件呢?其實有沒有這個化學反應條件的限制取決于我們如何來理解均相封閉體系的平衡狀態。如果我們把均相封閉體系理解為達到了完全的平衡狀態,則無需要求無化學反應這個限定條件;如果把均相封閉體系理解為只是達到了熱平衡、力平衡和宏觀上的化學組成平衡狀態,則還會因化學反應的存在,導致體系組成發生改變,即相當于反應物從系統中移出,而生成物從環境移入到體系。這樣,體系就等價于是一個開放體系了。同樣,對于非均相的封閉體系,只要已經達到了相平衡狀態,式(1)~式(4)是同樣成立的。有時我們之所以特意強調其適用條件為均相封閉體系是為避免一些特殊情況。例如,定組分汽液兩相封閉體系。當未達到汽液平衡時,宏觀上看其溫度、壓力和組成并不再隨時間發生變化,但體系可能會因吸熱或放熱發生氣液兩相量和組成的調整,從而引起導致狀態函數發生變化。
(二)記憶方法
夏億謙[5]、何展榮[6]、林金朝[7]曾分別提出熱力學基本關系式的多種不同的四邊形記憶法;王樹國[8]和宋小利[4]提出過坐標象限法,李德光[2]提出了雙四邊形法等。其中,筆者認為陳金友提出的記憶方法比較直觀易記[9]。熱力學四個基本關系式共涉及8個物理量,其中U,H,A和G為四個能量量綱函數;P,V,S和T為非能量量綱函數。如果把這8個物理量擺成圖1所示的圖形,則構成4條連接線。
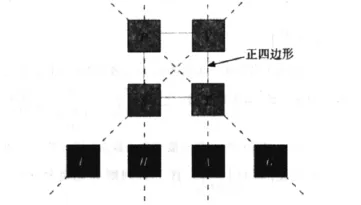
圖1 熱力學四個基本關系式的記憶圖
記憶規則:
(1)將P,V,S和T依次如圖1所示放在一個正四邊形的四個角上,然后將4個能量函數按U,H,A和G的順序擺成于正四邊形的下方,并做如圖所示的連接線。
(2)每個熱力學基本關系式的等式左邊是以每條連接線上的能量函數為因變量的微分,等式右邊是以連接線上的其它兩個物理量為自變量的微分并分別乘以處在正四邊形同橫邊上的另一個物理量后的加和。乘積項的正負取值方法為:當自變量處于正四邊形的左邊上時取正值,處于右邊時取負值。例如,和G處在同一連接上的兩個物理量是p和T,取其微分形式分別為dp和dT,分別乘以與其處在正四邊形同一橫邊上的物理量V和S,則為Vdp和SdT,因p處在正四邊形的左側邊上取為Vdp,而T在S的正四邊形的右側邊上,則取 -SdT。故dG=-SdT+Vdp。
二 Maxwell關系式
(一)推導與準確理解
Maxwell公式是將狀態函數用于熱力學四個基本關系式(式(1)~式(4))的必然結果。
狀態函數是指在一定的條件下系統的性質不再隨時間而變化(即達到平衡),此時狀態是唯一確定的,用于表征系統狀態的一系列物理量被稱為狀態函數(state function),如熱力學中常用的狀態函數有溫度(T)、壓力(p)、體積(V)、內能(U)、熱焓(H)、Gibbs自由能 (G)、Helmholtz自由能(A)和熵(S)等。狀態函數只是狀態的函數,即其從狀態1變化到狀態2時,其變化值只與狀態1和狀態2有關,而與所經歷的過程無關。
數學上狀態函數的變化量與無積分路徑無關。對于函數F=F(x,y),其全微分為

根據Gibbs相律,對于定組成的均相封閉體系,其自由度為2。故體系的任一狀態函數均可由其它兩個獨立的狀態函數來確定。例如,對于均相封閉體系的內能U可以通過選用 T,p,V,H,A,G,S 中任意兩個作為自變量來表達。表達時,需要注意因變量和自變量之間強度性質與容量性質的統一。選擇不同的自變量時表達式的簡潔程度不同,故常常選用S和V,S和p,T和V,T和p分別為U,H,A,G的兩個自變量。
例如設U=U(S,V),則全微分為

與式(1)相比較,知
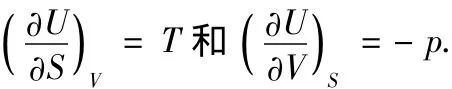
因為U為狀態函數,故應有
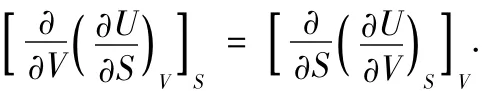
將上2式代入,則得到Maxwell關系式之一

同理,得到其它3個Maxwell關系式

式(13)~式(16)稱為Maxwell公式。它是在熱力學四個基本關系式的基礎上導出的,導出過程中未附加其它限制條件,故其使用范圍與四個基本關系式相同。
(二)記憶方法
關于Maxwell公式的記憶方法,文獻中已有多種[9-10]。例如金弼提出的“Pasvate”記憶法[11],何展榮提出的正四邊形法[6],辛凌云和王樹國等提出的“十字坐標法”[8,12],陳桂芳等人提出的對角關系法[10]。這里我們提出了一種邏輯上更清晰,簡潔易記的方法。
Maxwell公式共涉及 4 個狀態函數 (P,V,S,T),如果按排列組合關系共有24種取偏微分的方式,即4個狀態函數各出現在被求導函數、求導變量和不變量的位置上各一次,=24。Maxwell關系中已經出現了8種。根據偏導函數的性質

Maxwell公式還可寫出四個等價形式:
我們可以用圖2所示的三角形的三個頂點來表示被求導函數、求導變量和不變量的位置,用a,b和c分別表示三條邊。

圖2 三角形法表示偏導函數
這里我們提出一種記憶Maxwell關系的簡單方法。
(1)若S和T或者P和V同時出現在偏導函數的分子和分母上,即構成a邊的兩頂點,則不是Maxwell公式;
(2)若P和V或者S和T是構成c邊的兩頂點,則為Maxwell關系式的原式偏導數;
(3)若S和T或者P和V是構成b邊的兩頂點,則為Maxwell關系等價式偏導數。對于等價式偏導數,處理時需先取其倒數,化為Maxwell關系原型式;
(4)在P,V,S和T總共4個狀態函數中,Maxwell等式左端未出現的那個量就是等式右端的被求導函數,然后求導變量和不變量互換位置;
(5)Maxwell關系式中的正負號由旋轉方向來判斷。按p→V→S→T的順序,若等式兩端的偏微分函數旋轉方向相同則不出現負號,若旋轉相反則等式中出現一負號。
下面舉例說明
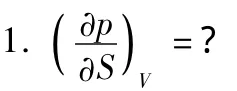
解:P和V出現在三角形的c邊上,故為Maxwell原型偏導數,則用缺少的T替代 p,然后 S和 V互換位置,得到為順時針旋轉方向(圖3),而 ()為逆時S針旋轉方向(圖4),為應有一負號出現。得出 ()=-V()。S

圖3 (為順時針旋轉方向V

圖4 ()為逆時針旋轉方向S

解:P和V出現在三角形的b邊上,故為Maxwell關系式的等價偏導數,需先取倒數,化為中未出現S,則等式的右端的被求導函數由S代替P,且T和V互換位置,寫出 ()。接下來判斷有無負號出現。T(為順時針方向(圖5),(為順時針方向(圖6),VT旋轉方向相同,故不會出現負號。即。最后寫出
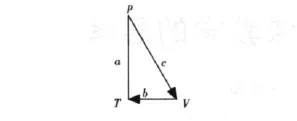
圖5 ()為順時針方向V
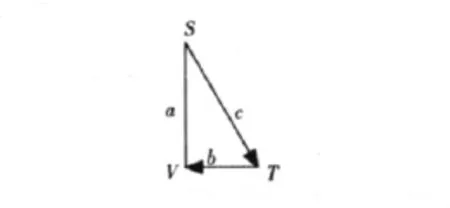
圖6 ()為順時針方向T

解:S和T同時處在a邊上,故不是Maxwell,需要尋求其它方法解決。因為S為被求導函數,且V為不變量,故應聯想到引入CV比較方便,由dU=TdS-pdV,兩邊在恒V下,同除以dT,得,故
[1]王秉章.一種新的熱力學函數定義式方陣圖和熱力學函數關系式信息圖[J].太原機械學院學報,1985(1):1-6.
[2]李德光.熱力學函數關系式圖解法[J].玉溪師專學報(綜合版),1987(6):48-51.
[3]朱華玲,石 軍,尹立輝,等.常見熱力學函數關系的圖形表達和簡圖記憶[J].天津農學院學報,2009,16(1):43-44.
[4]宋小利,李 梅.熱力學基本方程、對應系數關系式和麥克斯韋關系式的簡捷記憶[J].榆林學院學報,2008,18(2):74-75.
[5]夏億謙,程德聲.熱力學函數間關系的圖解[J].浙江師范學院學報(自然科學版),1982(5):99-100.
[6]何展榮.化學熱力學中幾個關系式的簡圖記憶法[J].川北教育學院院刊,1989(1):27-30.
[7]林朝金.熱力學函數關系式、全微分關系式和麥克斯韋關系式的簡捷記憶[J].四川師范大學學報(自然科學版),1995,18(6):96-97.
[8]王樹國,袁譽洪,李金林.熱力學函數關系式的坐標記憶法[J].廣東化工,2010,37(1):168.
[9]陳金友,易平貴,于賢勇.熱力學狀態函數關系式的記憶法[J].當代教育理論與實踐,2011,3(3):58-59.
[10]陳桂芳,高之清,李勝利,等.麥克斯韋關系式的簡捷記憶方法[J].廣東化工,2011,38(2):22-23.
[11]金 弼.關于maxwell關系式的邏輯記憶法[J].吉林農業大學學報,1984,6(4):52-55.
[12]辛凌云,李云平.巧記物理化學中的“麥克斯韋”關系式[J].洛陽師范學院學報,2008(5):180-182.

