帶有不可用區間的批運輸排序問題

許 尉，趙玉芳，岳雅娟

（沈陽師范大學 數學與系統科學學院，沈陽 110034）

0 引 言

在很多實際生產中，工件一般在處理機上加工后，若干個放在一起，形成一批，用車等工具運走，轉交到客戶手中，才算加工完。把這個時間稱為這批工件的交貨期，這樣的問題成為批運輸問題。在這個問題中，既要考慮工件的加工順序，還要決定如何分批，使目標函數達到最優，所以這個問題變得更為復雜。批運輸問題是Cheng等［1］首次提出的，對于單機、目標函數為總權提前懲罰與運輸費用之和問題，他們證明了這個問題是一般意義NP－難的。Cheng等［2］進一步給出了此問題的一個動態規劃算法，當批數有一個固定的上界時，這個算法是擬多項式的。對于極小化批運輸費用與工件的提早懲罰之和的單機分批排序問題，Cheng等［3］給出了這個問題與平行機排序問題的關系，從而把此問題歸類于平行機問題。對于目標函數是總加權提早與平均批運輸時間之和問題，Cheng等［4］證明是強NP－難的。Hermann等［5］考慮的是所有工件有一個公共工期的單機批運輸問題，對于總提早及延誤懲罰與誤工工件的運輸費用之和問題，給出了擬多項式動態規劃算法。當公共工期是一個決策變量時，Chen［6］給出了這個問題是多項式可解的。對于極小化總加權提早及延誤與誤工工件運輸費用之和的單機批運輸問題，Yun［7］證明是強NP－難的。Ji等［8］討論了在單機生產環境下的批運輸排序問題，總加權流水時間與運輸費用之和的問題是強NP－難的；當批數有一個上界時，該問題變為一般意義NP－難的。Wang等［9］研究了平行機生產環境下的批運輸排序問題，對于總流水時間與運輸費用之和問題，證明了一般情況下是強NP－難的，并給出了一個動態規劃算法。

機器由于維修或故障等原因會導致在某段時間內不可用，從而影響工件的加工過程，這種現象在排序問題中被稱之為機器可用性限制問題。Lee［10］研究了機器具有可用性限制的排序問題，討論了極小化加權總完工時間的單機及平行機排序問題，指出這2個問題都是NP－難的，給出啟發式算法，并分析了誤差界。對于不可用區間是已知的情況，Lee［11］考慮了2臺機器的流水作業排序問題，證明了時間表長問題是NP－難的，且給出了擬多項式動態規劃算法。Lee［12］進一步分別對可恢復和不可恢復的情況進行了討論，分析了問題的復雜性，給出了擬多項式動態規劃算法，并且對給出的啟發式算法進行了誤差界分析。Chen［13］研究了帶有有限個不可用區間且工件是不可恢復的單機排序問題，對于極小化總流水時間問題，給出了分枝定界算法。Kacem等［14］研究帶有一個固定的不可用區間限制且工件是不可恢復的排序問題，目標函數為總加權完工時間。對于該問題他們給出了一個全多項式時間近似算法（FPTAS）。對于同時帶有學習、惡化效應及可用性限制問題，趙玉芳等［15］給出了加權總完工時間擬多項式動態規劃算法。Zhao等［16］研究帶有速度維修的兩臺平行機的排序問題，當目標函數為總完工時間時給出多項式時間算法。Wang等［17］研究了機器帶有速度維修單機工期分配排序問題，對于極小化總提早、總延誤和共同的流余量費用問題給出多項式時間算法。Wang等［18］研究每臺機器都帶有惡化維修的排序問題，討論了極小化完工時間的絕對差值總和和等待時間的絕對值差值總和問題，并證明出它們是多項式時間可解的。Wang等［19］研究帶有一個惡化維修的平行機排序問題，他們給出目標函數為總完工時間的多項式時間算法。

本文將批運輸問題與機器的可用性限制結合在一起，并且運輸費用與批數有關，這個問題到目前為止還沒有人研究過。該問題不僅對實際生產具有指導意義，而且能夠豐富生產物流調度優化理論，具有一定的理論價值。

1 問題描述

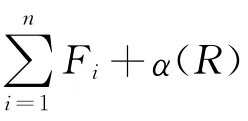
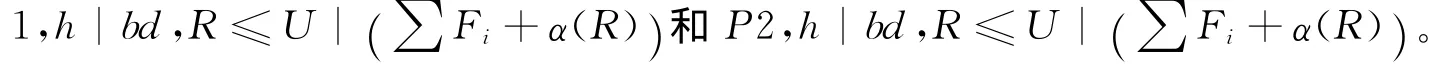
其中h表示帶有不可用區間限制的問題；bd表示批運輸問題；U為批數R的上界。

2 問題1，h｜bd，R≤U｜（ ∑Fi＋α（R））

對于工件是不可恢復的極小化總完工時間的單機排序問題，Adiri等［21］指出其問題是NP－難的。那么對于目標函數是總流水時間的問題，至少為NP－難的。故可得到下面結論。

對于單機帶有不可用區間目標函數為

引 理 1 問 題 1，h｜bd，R≤U｜（∑Fi＋α（R）） 存在一個最優解π＊＝〈B1，…，BR〉滿足

1）在T1前和T2后的工件分別按SPT規則排列；

圖1 問題1，h｜bd，R≤U｜ （∑Fi＋α（R））的例圖

2）Bl包含所有在（Dl－1，Dl］之間完工的工件。

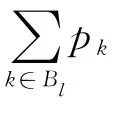
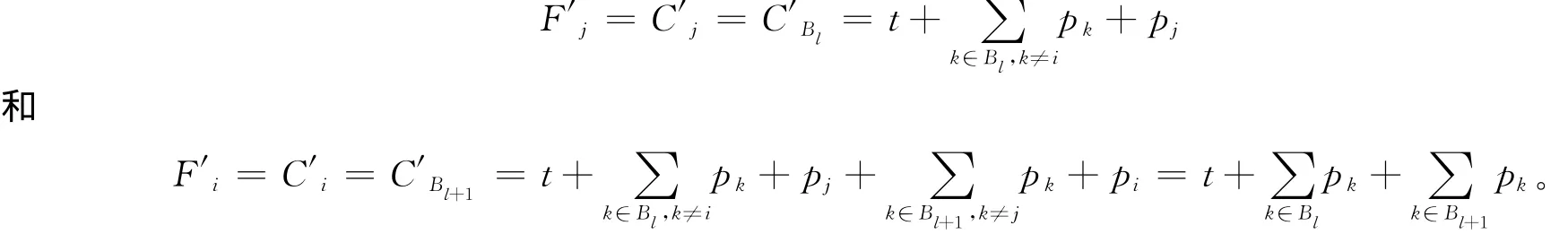
其他批的完工時間不變，則有＝；由pi＞pj可知，＜，其余批不變。即第l批前的工件流水時間不變，第l批的工件的流水時間減少，第l批后的工件流水時間也不變。從而G（π＊）＞G（π′），所以與假設π＊為最優序列矛盾。于是，存在一個最優序列π＊，使得T1前的工件按SPT規則排列。同理可證在T2后的工件也滿足SPT規則排列。從而存在一個最優解π＊滿足在T1前和T2后的工件分別按SPT規則排列。

下面用反證法證明2）。不失一般性，設最優序列π＊中工件的加工順序為J［1］，J［2］，…，J［n］，其中J［j］表示π＊中第j個加工的工件。Bl批的交貨期為，則＜…＜＜…＜。假設存在一個工件J［j］滿足＜≤且不在Bl批中加工，由于工件J［j］在Bl批之前沒有完工，則有＞。若把工件J［j］放在Bl批中，設為新序列π′，其他工件的加工順序與所在批不變，則有＝，，從而G（π＊）＞G（π′），與π＊為最優排序矛盾。在其他批中的工件按照同樣的討論，可以證明存在一個最優排列，使得所有批都是由一些連續完工的工件組成的。在任意的最優排列中，因為所有在Dl處完工的工件，都可以被分到Bl中，l＝1，…，R。Bl應包含在（Dl－1，Dl］完工的所有工件。

由于同批中的所有工件的流水時間相同，可以得到下面的結論。

引理2 對于問題1，h｜bd，R≤U｜ （∑Fi＋α（R）） 任何一個最優序列，每一批內的工件加工順序是任意的。所以＞。又因為

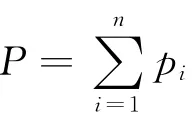
1）當工件Jj排在［0，T1］區間內，有

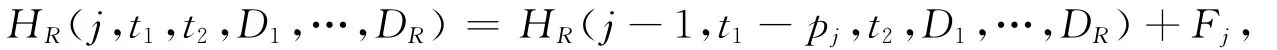
其中Fj＝｛Dl｜Dl－1＜t1≤Dl，D0＝0，l＝1，…，R｝；

2）當工件Jj排在T2后，有

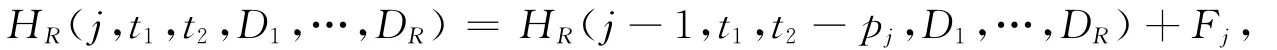
其中Fj＝｛Dl｜Dl－1＜t2＋T2≤Dl，D0＝0，l＝1，…，R｝。

由以上分析可得動態規劃算法如下：

在下述動態規劃算法中，設

算法DP1：

1）把工件按SPT序編號，使p1≤p2…≤pn；

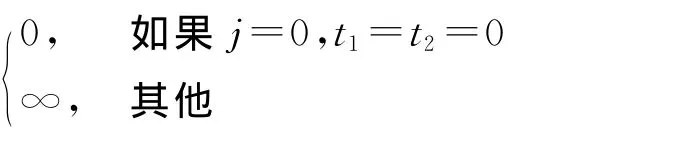
3）按遞歸方程：

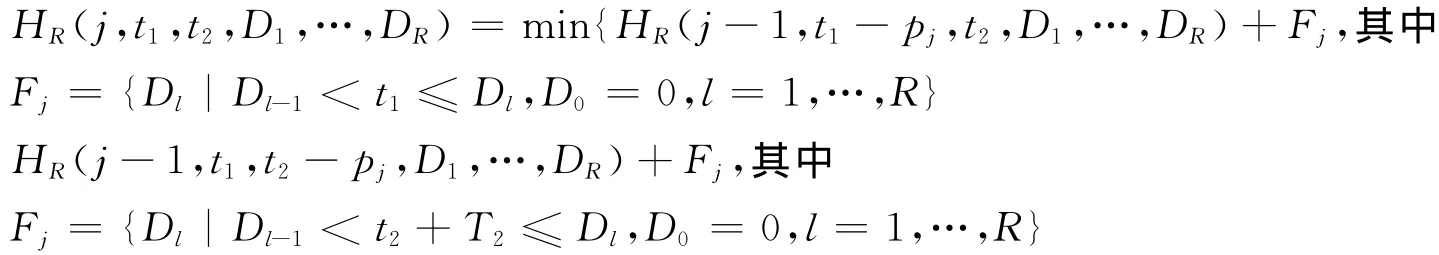
其中j＝0，…，n，t1＝0，…，T1，t2＝0，…，P，Dl＝Dl－1＋1，…，T2＋P，l＝1，…，R，D0＝0；

4）G＊＝min｛HR（n，t1，t2，D1，…，DR）＋α（R）｝，利用反向追蹤得到最優排序及分批，R＝1，…，U。

引理3 動態規劃算法DP1的時間復雜性為O（nU2T1（T2＋P）U）。

證明 在狀態（j，t1，t2，D1，…，DR）下HR（j，t1，t2，D1，…，DR）中j的取值為1，2，…，n；t1的取值為0到T1，則t2在t1取定之后便可確定；D1到DR可取到的最大值都為T2＋P，R＝1，…，U；從而遞推關系式的不同狀態R＝1，…，U至多有nT1（T2＋P）U。對于每個狀態，遞推關系式的右邊可以在O（U）時間內被計算。因此，整個的計算復雜性為O（nU2T1（T2＋P）U）。

3 問題P2，h｜bd，R≤U｜ （∑Fi＋α（R））

王國慶等［9］已經證明出問題P2｜bd，R≤U｜ （∑Fi＋α（R）） 為NP－難的，在此基礎上加入一個不可用區間，可得下面結論。

定理2 問題P2，h｜bd，R≤U｜ （∑Fi＋α（R）） 至少是NP－難的。

引理4 問題P2，h｜bd，R≤U｜ （∑Fi＋α（R）） 存在一個最優解π＊＝〈B1，…，BR〉滿足

1）在M1上的T1前和T2后與M2上加工的工件分別按SPT規則排列；

2）Bl批中包含所有在（Dl－1，Dl］之間完工的工件，l＝1，…，R。

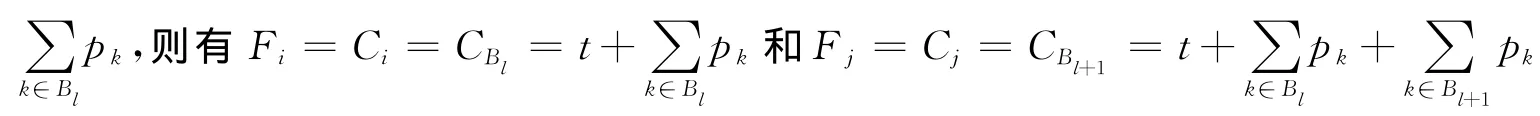
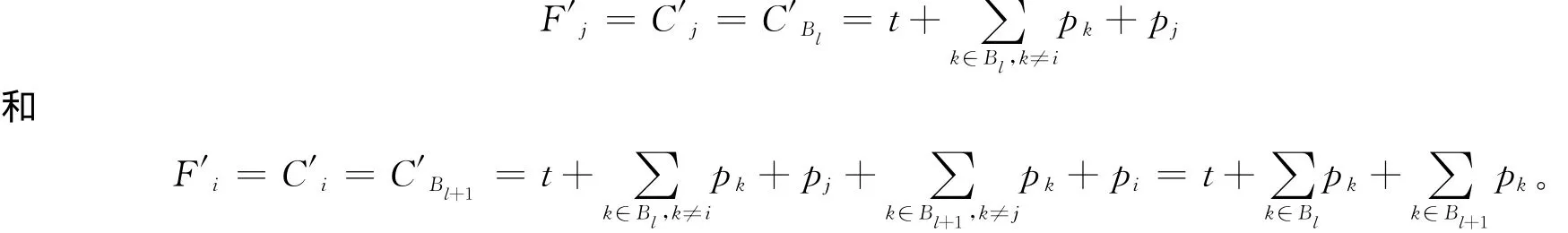
其他批的完工時間不變，則有＝；由pi＞pj可知，＜其余批不變，第l批前的工件流水時間不變，第l批的工件的流水時間減少，第l批后的工件流水時間也不變。從而G（π＊）＞G（π′），所以與假設π＊為最優序列矛盾。綜上所述，可以證明出存在一個最優解使得在M1上的T1前和T2后與M2上加工的工件分別按SPT規則排列。

2）同引理1中2）的證明。

而對于2臺平行機的情況下，機器由于維修或故障，會導致機器在一段時間內不可用，在這種機器受限的情況下，假設只有1臺機器受限。那么把問題劃分為2類，一類是機器中途維修；另一類是機器中途損壞，即懂某一刻開始一直不可用。具體描述如下：

3.1 機器中途維修

圖2 問題3.1的實例

對于第一類情況（如圖2所示）。

由引理4可知，對于問題P2，h｜bd，R≤U｜（∑Fi＋α（R）） 的第一類情況，存在最優排序，在M1上的T1前和T2后與M2上的工件的加工順序都按SPT排列。那么將工件分成3部分，分別在M1上的T1前和T2后與M2上，使每一部分工件都按SPT排列，從而得到最優排序。據此，可以建立求解這個問題的動態規劃算法。

在下述動態規劃算法中，假設工件J1…Jj已排完，定義HR（j，t1，t2，t3，D1，…，DR）為已排列工件J1到Jj的最小總流水時間，使得在M1上T1前的總加工時間為t1（t1＜T1），在M1上T2后總加工時間為t2，則當前在T2后最后一個工件的完工時間為t2＋T2，在M2上工件的總加工時間為t3，Bl的交貨期為Dl，l＝1，…，R。于是，工件J1…Jj的總流水時間分以下3種情況：

1）當工件Jj排在M1上的［0，T1］區間內，有

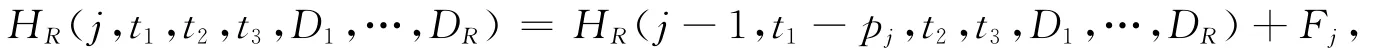
其中Fj＝｛Dl｜Dl－1＜t1≤Dl，D0＝0，l＝1，…，R｝；

2）當工件Jj排在M1上的T2后，有

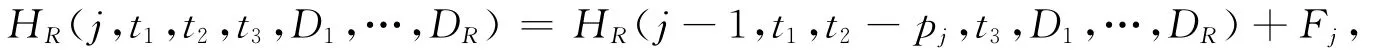
其中Fj＝｛Dl｜Dl－1＜t2＋T2≤Dl，D0＝0，l＝1，…，R｝；

3）當工件Jj排在M2上，有

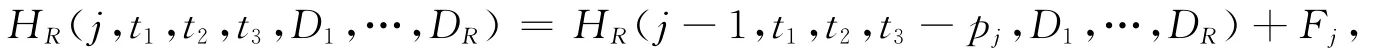
其中Fj＝｛Dl｜Dl－1＜t3≤Dl，D0＝0，l＝1，…，R｝。

由以上分析可得動態規劃算法如下：

算法DP2：

1）把工件按SPT序編號，使p1≤p2…≤pn；

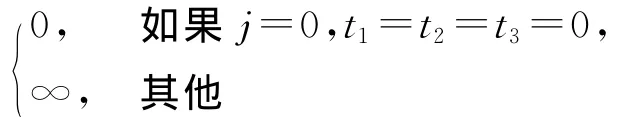
3）按遞歸方程：

其中j＝0，…，n，t1＝0，…，T1，t2＝0，…，P，t3＝0，…，P，Dl＝Dl－1＋1，…，T2＋P，l＝1，…，R，D0＝0；

4）G＊＝min｛HR（n，t1，t2，t3，D1，…，DR）＋α（R）｝，利用反向追蹤得到最優排序及分批R＝1，…，U。

引理5 動態規劃算法DP2的時間復雜性為O（nT1PU2（T2＋P）U）。

證明 在狀態（j，t1，t2，t3，D1，…，DR）下HR（j，t1，t2，t3，D1，…，DR）中j的取值為1，2，…，n；t1的取值為0到T1，而t2的取值為0到P，從而t3便可被確定下來；D1到DR可取到的最大值都為T2＋P，R＝1，…，U；從而遞推關系式的不同狀態至多有nT1P（T2＋P）U。對于每個狀態下Fj可以在O（U）時間內被計算。因此，整個的計算復雜性為O（nU2T1（T2＋P）U）。

3.2 機器中途損壞

圖3 問題3.2的實例

對于第二類情況（如圖3所示）。

由引理4可知，對于問題P2，h｜bd，R≤U｜（∑Fi＋α（R）） 的第二類情況，存在最優排序，在M1上的T1前與M2上的工件的加工順序都按SPT排列。那么可以將工件分成2部分，分別在M1上的T1前和M2上，使每一部分工件都按SPT排列，從而得到最優排序。據此，可以建立求解這個問題的動態規劃算法。

在下述動態規劃算法中，假設工件J1…Jj已排完，定義HR（j，t1，t2，D1，…，DR）為已排列工件J1到Jj的最小總流水時間，使得在M1上T1前的總加工時間為t1（t1＜T1），在M2上工件的總加工時間為t2，Bl的交貨期為Dl，l＝1，…，R。于是，工件J1，…，Jj的總流水時間分以下兩種情況：

1）當工件Jj排在M1上的［0，T1］區間內，有

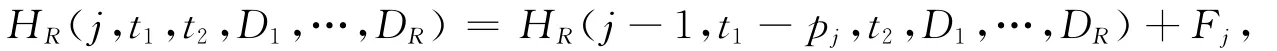
其中Fj＝｛Dl｜Dl－1＜t1≤Dl，D0＝0，l＝1，…，R｝；

2）當工件Jj排在M2上，有

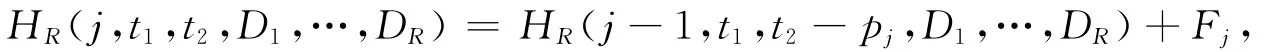
其中Fj＝｛Dl｜Dl－1＜t3≤Dl，D0＝0，l＝1，…，R｝。

由以上分析可得動態規劃算法DP3如下：

1）把工件按SPT序編號，使p1≤p2…≤pn；

3）按遞歸方程：

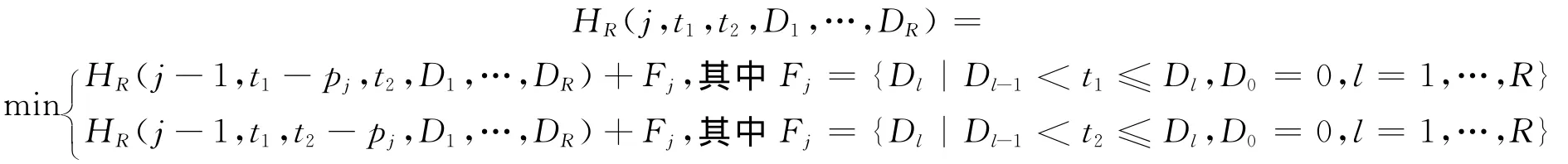
其中j＝0，…，n，t1＝0，…，T1，t2＝0，…，P，Dl＝Dl－1＋1，…，T2＋P，l＝1，…，R，D0＝0；

4）G＊＝min｛HR（n，t1，t2，D1，…，DR）＋α（R）｝，利用反向追蹤得到最優排序及分批，R＝1，…，U。

引理6 動態規劃算法DP3的時間復雜性為O（nT1U2PU）。

證明 在狀態（j，t1，t2，D1，…，DR）下HR（j，t1，t2，D1，…，DR）中j的取值為1，2，…，n；t1的取值為0到T1，則t2在t1取定之后便可確定；D1到DR可取到的最大值都為P，R＝1，…，U；從而遞推關系式的不同狀態R＝1，…，U至多有nT1PU。對于每個狀態，遞推關系式的右邊可以在O（U）時間內被計算。因此，整個的計算復雜性為O（nT1U2PU）。

4 結 論

本文研究了單機和2臺平行機帶有不可用區間的批運輸問題，其中機器有可用性的限制。通過分析，證明了此類問題至少是NP－難的。為此給出了此類問題的擬多項式動態規劃算法，并給出了時間復雜性及相應的數值例子。為了進一步的研究，需要值得考慮的是單機及平行機情況下是否是強NP－難的。對于這兩種情況是否能找到一個FPTAS方案。

［1］CHENG T C E，KAHLBACHER H G.Scheduling with delivery and earliness penalties［J］.Asia－Pacific J Oper Res，1993，10（2）：145－152.

［2］CHENG T C E，GORDON V S.Batch delivery scheduling on a single machine［J］.J Oper Res Soc，1994，45（10）：1211－1215.

［3］CHENG T C E，GORDON V S，KOVALYOV M Y.Single machine scheduling with batch deliveries［J］.Eur J Oper Res，1996，94（2）：277－283.

［4］CHENG T C E，KOVALYOV M Y，Lin B M T.Single machine scheduling with batch delivery and job earliness penalties［J］.SIAM J Optim，1997，7（2）：547－559.

［5］HERMANM J W，LEE C Y.On scheduling to minimize earliness－tardiness and batch delivery costs with a common due date［J］.Eur J Oper Res，1993，70（3）：272－288.

［6］CHEN Zhilong.Scheduling and common due date assignment with earliness－tardiness penalties and batch delivery costs［J］.Eur J Oper Res，1996，93（1）：49－60.

［7］YUAN Jinjiang.A note on the complexity of single－machine scheduling with a common due date，earliness－tardiness，and batch delivery costs［J］.Eur J Oper Res，1996，94（1）：203－205.

［8］JI Min，HE Yong，CHENG T C E.Batch delivery scheduling with batch delivery cost on a single machine［J］.Eur J Oper Res，2007，176（2）：745－755.

［9］WANG Guoqing，CHENG T C E.Parallel machine scheduling with batch delivery costs［J］.Int J Prod Econ，2000，68（2）：177－183.

［10］LEE C Y.Machine scheduling with an availability constraint［J］.J Global Optim，1996，9（3／4）：395－416.

［11］LEE C Y.Minimizing the makespan in the two－machine flowshop scheduling problem with an availability constraint［J］.Oper Res Lett，1997，20（3）：129－139.

［12］LEE C Y.Two－machine flowshop scheduling with availability constraints［J］.Eur J Oper Res，1999，114（2）：420－429.

［13］CHEN W J.Minimizing total flow time in the single－machine scheduling problem with periodic maintenance［J］.J Oper Res Soc，2006，57：410－415.

［14］KACEM I，HAOUARI M.Fully polynomial time approximation scheme for the weighted flow－time minimization on a single machine with a fixed non－availability interval［J］.Comput Indust Eng，2009，56（4）：1708－1712.

［15］崔苗苗，趙玉芳，王松麗.機器具有可用性限制的加權總完工時間問題［J］.沈陽師范大學學報：自然科學版，2012，30（2）：157－163.

［16］ZHAO Chuanli，TANG Hengyong，CHENG Congdian.Two－parallel machines scheduling with rate－modifying activities to minimize total completion time［J］.Eur J Oper Res，2009，198（1）：354－357.

［17］WANG Xiaoyuan，WANG Mingzheng.Single machine common flow allowance scheduling with rate－modifying activities［J］.Comput Indust Eng，2010，59（4）：898－902.

［18］WANG Jibo，WEI Caimin.Parallel machines scheduling with a deteriorating maintenance activity and total absolute differences penalties［J］.Appl Math Comput，2011，217（20）：8093－8099.

［19］WANG J J，WANG J B，LIU F.Parallel machines scheduling with a deteriorating maintenance activity［J］.J Oper Res Soc，2011，62：1898－1902.

［20］GRAHAM R L，LAWLER E L，LENSTRA J K，et al.Optimization and approximation in deterministic sequencing and scheduling：A survey［M］.Amesterdam：North－Hollard，1979，5：287－326.

［21］ADIRI I，BRUNO J，FROSTIG E，et al.Single machine flow－time scheduling with a single breakdown［J］.Acta Inform，1989，26（7）：679－696.