Robust exponential stabilityanalysis of discrete－time switched Hopfield neural networks with time－varyingdelay

，

（School of Mathematics and System Science，Shenyang Normal University，Shenyang 110034，China）

0 Introduction

Switched systems are an important class of hybrid dynamical systems which are composed of a family of continuous－time or discrete－time subsystems and a rule that orchestrates the switching among them.Lots of valuable results in the stability analysis and stabilization for linear or nonlinear hybrid and switched systems were established；see［1－3］and the references cited therein.Recently，the switched Hopfield neural networks，whose individual subsystems are a set of Hopfield neural networks，have found applications in the field of combinatorial optimization，knowledge acquisition and pattern recognition［4－10］.This motivated many researchers to study the stability issues of switched neural networks［11－15］.In ［14］，the robust exponential stability analysis of discrete－time switched Hopfield neural networks with time delay is considered.However，the case of time－varying delay has not been available in the literature so far，which motivates us to carry out the present study.

1 Problem formulation and preliminaries

In this section，we will consider the model of discrete－time switched Hopfield neural networks with time－varying delay and uncertainty：

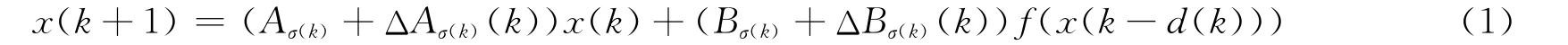
Whereσ（k）is a switching signal which takes its values in the finite setN＝｛1，2，…，n｝.u（k）＝（u1（k），u2（k），…，un（k））T∈Rnis the state vector of the neurons，A＝diag｛a1，a2，…，an｝are the state feedback coefficient matrix；B＝（bij）n×nis the connection weight matrix.f（·）＝（f（·），f（·），…，f（·））T∈Rnis the neuron activation function.The positive integerd（k）denotes the time－varying discrete delay satisfying

The initial condition associated with model（1）is given by

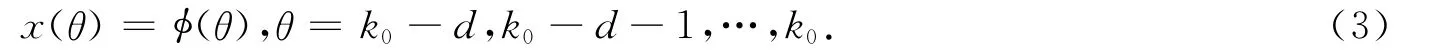
Throughout this paper，we have the following assumptions

1）Forj＝｛1，2，…，n｝，the neuron activation functionsfj（·）are continuous and bounded.

3）The parameter uncertaintiesΔAi（k），ΔBi（k）are unknown but norm bounded，and satisfy

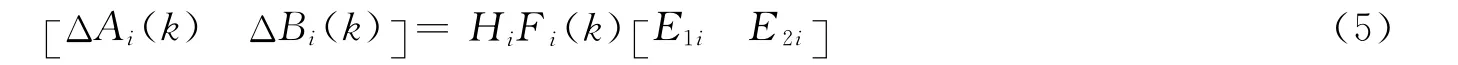
WhereFi（k）is an unknown real time－varying matrix and satisfies the following bound condition：

4）The switching sequence is defined asζ＝ ｛xk0；（i0，k0），（i1，k1），…，（im，km），…｝，whenk∈［k>m，km＋1），theimth subsystem is activated and the states of system （1）do not jump when the switch occurs.

For our development，we need the following definitions and lemmas.

Definition 1［14］The discrete－time switched Hopfield neural network （1）is said to be robustly exponentially stable if its solution satisfies

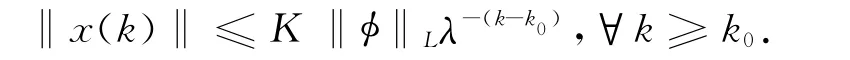
for any initial condition （k0，φ）∈R＋×Cnand parameter uncertainty satisfying （5）.‖φ‖L＝supk0－d≤l≤k0‖φ（l）‖，K＞0is the coefficient，andλ＞1is the decay rate.

Definition 2［16］For anyk≥k0and any switching signalσ（s），k0≤s≤k，letNσdenote the switching numbers ofσ（s）during the interval［k0，k］.If there existN0≥0andTa＞0such thatNσ（k0，k）≤N0＋（k－k0）／Ta，thenTaandN0are called the average dwell time and the chatter bound，respectively.

Without loss of generality，in this paper，we assumeN0＝0for simplicity.

Lemma 1［3］For any constant matrixW＝WT≥0，two positive integersrandr0satisfyingr≥r0≥1，the following inequality

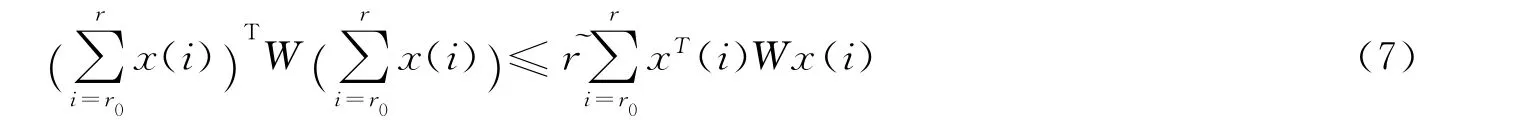
Lemma 2［17］LetA，D，MandWbe real matrices which have appropriate dimensions such thatW＞0andFTF≤I.For any scalarε＞0such thatW－εDDT＞0，then we have the following inequality：（A＋DFM）TW－1（A＋DFM）≤AT（W－εDDT）－1A＋ε－1MTM.（8）

2 Main results

In this section，the robust exponential stability criteria for the discrete－time switched Hopfield neural networks（1）will be presented using an average dwell time method.Firstly，consider the ithsubsystem ，that is，whenσ（k）＝i，

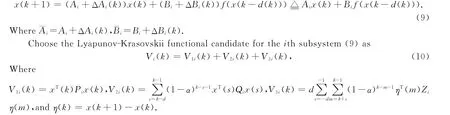
Now we give the following theorem，which plays an important role in the derivation of the robust exponential stability condition for system （1）.

Theorem 1Under the assumptions（ⅰ）－（ⅳ），for given scalars 0＜α＜1，μ≥1，system （1）is robustly exponentially stable，if there exist diagonal matricesΛ＝diag｛λ1，λ2，…，λn｝＞0，and positive matricesPi＞0，Qi＞0，Zi＞0，and scalarsε1i＞0，ε2i＞0，i∈N，such that the following inequalities hold：

Whicheidenotes the unit column vector having“1”element on itsith row and zeros elsewhere.Namely，

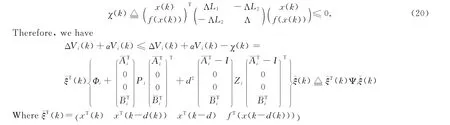
and

According to Definition 1，system （1）is robustly exponentially stable.This completes the proof of Theorem 1.

3 Illustrative examples

Example Consider the discrete－time switched Hopfield neural networks （1）with the following parameters：

E21＝E22＝E23＝diag｛0.03，0.04，－0.05｝，Fi（k）＝diag｛sin（k），sin（k），sin（k）｝，i＝1，2，3，The activation functions are taken as

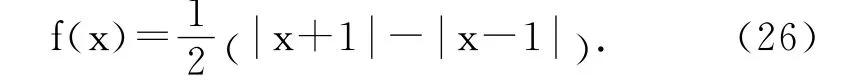
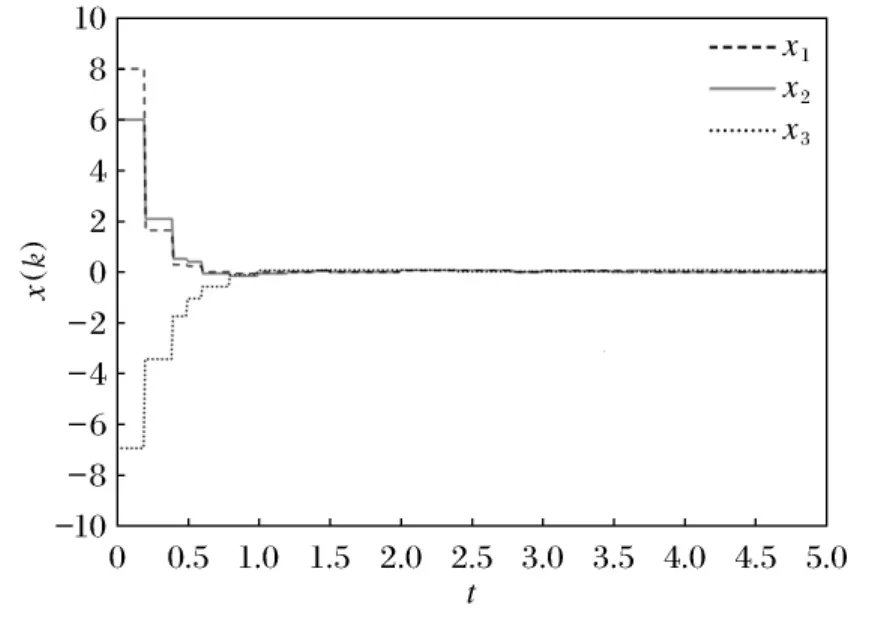
Fig.1 State of response of system （7）with（34）

Choosingα＝0.4，μ＝1.2，d＝1.5，Solving the conditions（11），（12），（13），it is found that the linear matrix inequalities are feasible.We obtain that＝0.3569，on the basis of（14），we have that＝0.4is satisfied.

On the basis of （25），there are three subsystems in the switched system （1）.In the simulation，let k0＝0，d（k）＝1.5＊sin（k）.Take the switching sequence as 321321321…….It can be seen from the switched sequence that Ta＝0.5.

Choosing the initial value as φ（s）＝［8 6 －7］T，we then obtain Fig.1，which depicts the trajectories of the system state.

4 Conclusions

This paper is concerned with the robust exponential stability problem for discrete－time switched Hopfield neural networks with time－varying delay and uncertainty.A numerical example is provided to demonstrate the potential and effectiveness of the results obtained.

［1］LIBERZON D，MORSE A S.Basic problems in stability and design of switched systems［J］.IEEE Control Systems Magazine，1999，19（5）：59－70.

［2］YE H，MICKEL N，HOU L.Stability theory for hybrid dynamical systems［J］.IEEE Trans Autom Control，1998，43（4）：461－474.

［3］李巖，劉玉忠.具有時變時滯不確定切換系統的魯棒鎮定［J］.沈陽師范大學學報：自然科學版，2011，29（2）：142－145.

［4］LI Hongyi，WANG Chuan，SHI Peng，et al.New passivity results for uncertain discrete－time stochastic neural networks with mixed time delays［J］.Neurocomputing，2010，73（16／17／18），3291－3299.

［5］LIU Yurong，WANG Zidong，LIU Xiaohui.Asymptotic stability for neural networks with mixed time delays：the discrete－time case［J］.Neural Netw，2009，22（1），67－74.

［6］WU Zhengguang，SHI Peng，SU Hongye.Delay－dependent exponential stability analysis for discrete－time switched neural networks with time－varying delay［J］.Neurocomputing，2011，74（10）：1626－1631.

［7］LIU Yurong，WANG Zidong，SERRANO A.Discrete－time recurrent neural networks with time－varying delays：Exponential stability analysis［J］.Phys Lett A，2007，362（5／6）：480－488.

［8］HUANG He，QU Yuzhong，LI Hanxiong.Robust stability analysis of switched Hopfield neural networks with time－varying delay under uncertainty［J］.Phys Lett A，2005，345（4）：345－354.

［9］ZONG Guangdeng，LIU Jia，ZHANG Yunxi.Delay－range－dependent exponential stability criteria and decay estimation for switched Hopfield neural networks of neural type［J］.Nonlinear Analysis，2010，4（3）：583－592.

［10］SUN Jian，LIU G P，CHEN Jie.Improved delay－range－dependent stability criteria for linear systems with time－varying delays［J］.Automatica，2010，46（2）：466－470.

［11］AHN C K.Switched exponential state estimation of neural networks based on passivity theory［J］.Nonlinear Dyn，2012，67（1）：573－586.

［12］LIAN Jie，ZHANG Kai.Exponential stability for switched Cohen－Grossberg neural networks with average dwell time［J］.Nonlinear Dyn，2011，63（3）：331－343.

［13］AHN C K.AnH∞approach to stability analysis of switched Hopfield neural networks with time－delay［J］.Nonlinear Dyn，2010，60（4）：703－711.

［14］HOU Linlin，ZONG Guangdeng，WU Yuqiang.Robust exponential stability analysis of discrete－time switched Hopfield neural networks with time delay［J］.Nonlinear Analysis：Hybrid Systems，2011，5（3）：525－534.

［15］ZHANG Dan，YU Li.Passivity analysis for discrete－time switched neural networks with various activation functions and mixed time delays［J］.Nonlinear Dyn，2012，67（1）：403－411.

［16］SONG Yong，FAN Jian，FEI Minrui，et al.RobustH∞control of discrete switched systems with time delay［J］.Appl Math Comput，2008，205（1）：159－169.

［17］XU Shengyuan，CHEN Tongwen.RobustH∞control for uncertain discrete－time stochastic bilinear systems with Markov switching［J］.Internat J Robust Nonlinear Control，2005，15（5）：201－217.