Exponential stabilityfor switched systems with mutiple time-varingdelays
, zhong
(School of Mathmatics and System Science,Shenyang Normal University,Shenyang 110034,China)
0 Introduction
As an important class of hybrid dynamical systems,switched systems consist of a family of subsystems described by differential or difference eauations and a logical rule that orchestrates the switching mechanism between these subsystems.Switched systems arise in many practical models in manufacturing,communication networks,automotive engine control,chemical processes and so on[1-2].
During the previous decade,the stability problem of switched linear systems has attracted a lot of attention[3-4].For stability issues,two main problems haves been investigated in known literatures.One is to find conditions that guarantee asymptotic stability of the switched systems for arbitrary switching.The other is to identify those switching signals for which the switched systems is asymptotically stable if it is not asymptotically stable for arbitrary switching.The main approach for stability analysis relies on the use of Lyapunov-Krasovskii functionals and LMIs approach for construting common Lyapunov function[5].
Time delay is often encountered in various engineering systems.It has been well recognised that the presence of time delay may result instability and poor performance of a control system[6-9].For switched systems,because of the complicated behavior caused by the interaction between the continous dynamics and discrete switching,the problem of time delays is more difficult to study,while it has a wider range of application in engineering.So reseaching the switched systems with timedelay has more important theoretical and practical significance.
Recently,some results have appeared on stability analysis,controller and robust filtering design for switched systems with time delay in the open literature[10-14].Sun et al.[10]studied the stability and L2-gain analysis for a class of switched systems with time-delay.In terms of a set of linear matrix inequalities,some sufficient conditions are obtained by average dwell time.The exponential stability problem was considered in[17]for switched linear system with impulsive effects by using matrix measure concept.Although many important results have been obtained for switched linear systems,there are few results concerning the stability of the system with multiple time-varing delays[17].The paper[15]just considered the switched systems with multiple time-delay,and the time-varing delay is not considered.
In this paper,we investigate the problem of the exponential stability for switched systems with multiple time-varing delays.Based on a piecewise Lyapunov-Krasovskii functional,and taking the measure of average dwell time,a new sufficent condition for robust exponential stability is obtained.The sufficient conditions are given in the form of LMIs that can be solved easily.The result is proven to be valid by the simulation at last.
1 preliminaries
Consider the following switched systems which consist of m subsystems with multiple timevarying delays.Without the general,we just consider the systems with two time-varying delays as:
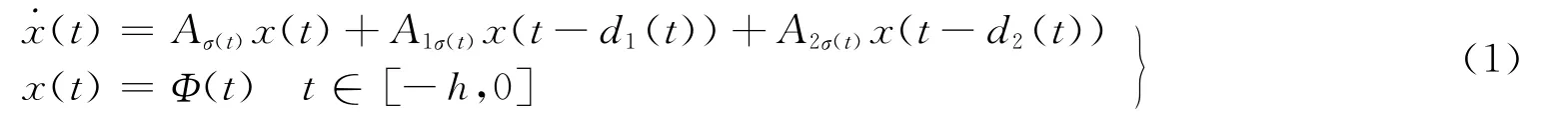
Wherex(t)∈Rnis the state,σ(t):[0,+∞]→M={1,2,…,m}is switching signal;mis a natural number that denotes the number of the subsystems.Ai∈Rn×n,A1i∈Rn×n,A2i∈Rn×nare systems matrices and time-varying delay matrices with appropriate dimensions forith subsystem.The initial condition is continuous vector valued function int∈[-h,0],h∈max{hi}.di(t)is the time-varying delays of the system and satisfies following conditions:
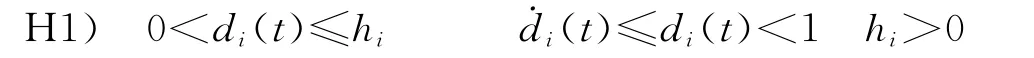
If the swiched systems have structural uncertainties,they can be described as following:
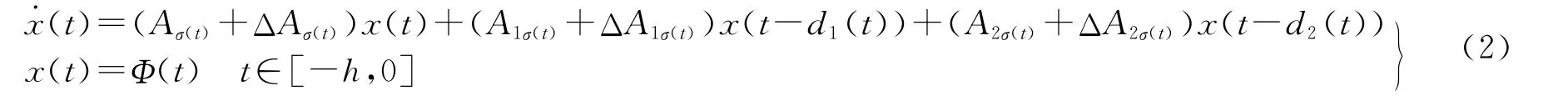
And the time-varying structural uncertainties have the form as following:
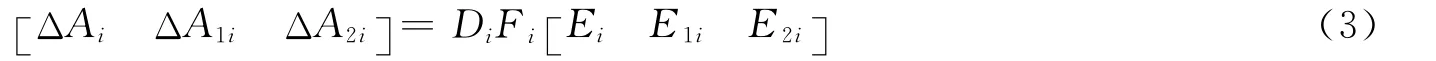
WhereDi,Ei,E1iandE2iare contant matrice with appropriate dimensions.Fi(t)are time-varying unknown matrices,and satisfyingFTiFi≤I,?t∈R,i∈M,whichIis an identical matrix with apropriate dimensions.
Lemma 1[14]Assume that H1holds,then,for anyx(t)solution to system (1)and constant matrixesWi>0,the following inequality holds:
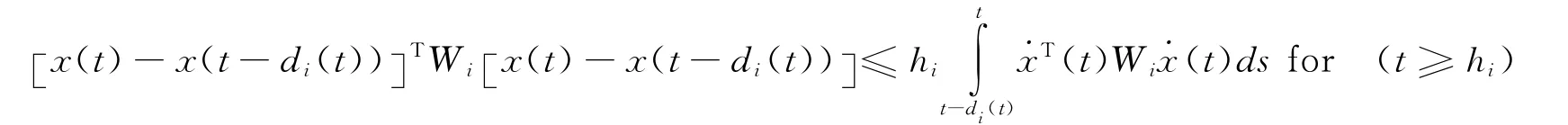
Lemma 2[15]For any matricesP,E,F,HwithP>0,FTF≤I,and scalarε>0,one has:EFH+HTFTET≤ε-1EET+εHTH.
Corresponding to the switching signalσ(t),we have the swiching sequence:
2 Main results
2.1 Exponential stability of switched systems
The sufficient condition of the multiple time-varying delays exponential stability for the switched systems(1)is given below.
Theorem 1For scalarsh1>0,h2>0,andα>0,if there exist matricesPi>0,Q1i>0,Q2i>0,Z1i>0Z2i>0such that the following LMIs hold:

Then the switched system (1)are exponentially stable for any switching law satisfying the average dwell timeTα>=lnμ/α.
Further more,the decay of the state is

Therefore,theorem 1holds.
2.2 Robust exponential stability of the uncertian switched systems
The sufficient condition of robust exponential stability for the uncentain switched systems(2)given as following.
Theorem 2For scalarsh1>0,h2>0,andα>0,if there exist matricesPi>0,Q1i>0,Q2i>0,Z1i>0,Z2i>0,such that the following LMIs hold,then the systems(2)is robust exponential stability.
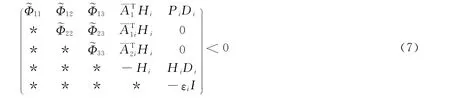
And the uncertain swiched systems(2)are saitisfying the average dwell timeTα>T*α=lnμ/α.
Furthermore,the decay of the state is
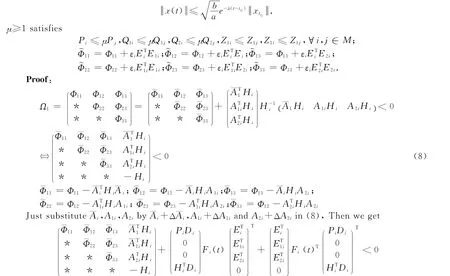
From the lemma 2,there exist a positive scaleεi(i∈M),we can obtain that the above inequality holds if and only if(9)is holded.
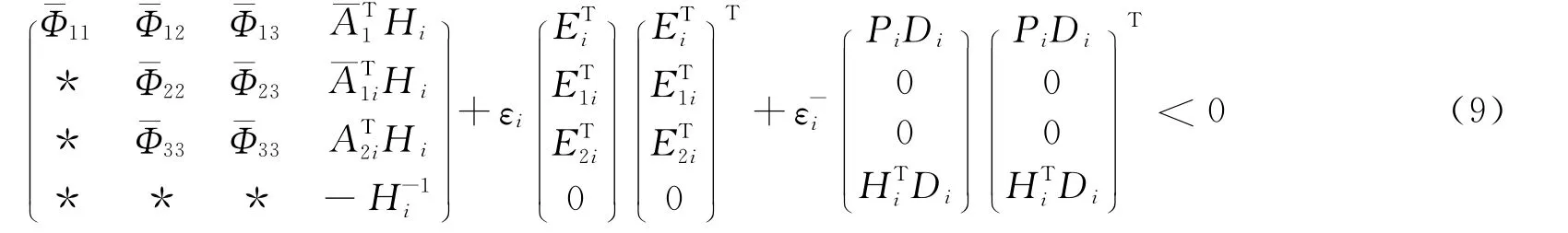
The equality(9)holds if and only if(7)holds through Shur complementary lemma.The last proof is similar to the process of theorem 1.
3 Numerical example and simulatiom
Example:Comsider system (1)for the following parameters:

Chooseα=0.5,μ=1.2according to Theorem 1,solving LMIs (6)leads to the following feasible solutions:
Then=lnμ/α=0.364 6.And we can obtain that:‖xt‖≤2.075‖xt0‖.Let the initial state bex0=(-3 2)T,The simulation for the curves of the state is given in Fig.1.

Fig.1 The curves of the state x(t)
4 Conclusions
In this paper,the exponential stability and robust exponential stability for switched system with multiple time-varing delays have been presented in terms of LMIs.Based on the average dwell time method,the sufficient conditions for the multiple time-varing delays has been obtained.Moreover,with a piecewise Lyapunov-Krasovskii functional proposed,we have obained a less conservative and more general results than the literature[16].And the effectivness of the proposed method has been verified by a simulation example.Finally,the state feedback problem is an open question.
[1]BRANICKY M S.Multiple Lyapunov functions and other analysis tools for switched and hybrid systems[J].IEEE Trans on Autom Contr,1998,43(4):475-482.
[2]LI Yan,LIU Yuzhong.Robust stabilization analysis for uncertain switched systems with time-varying delay[J].沈陽師范大學學報:自然科學版,2011,29(2):142-145.
[3]DECARLO R A,BRANICKY M S.Perspective and results on stability and stabilization of hybrid systems[J].Proc IEEE,2000,88(7):1069-1082.
[4]LIBERZON D,MORSE A S.Basic problems in stability and design of switched systems[J].IEEE Contr Syst Magazine,1999,19(5):59-70.
[5]SHORTEN R N,NARENDRA K S.On the stability and existence of common Lyapunov functions for stable switching systems[C]∥Decision and Contr,1998:3723-3724.
[6]SEHJEONG K,CAMPBELL S A,LIU X Z.Stability of a class of linear switching systems with time delay[J].IEEE Trans on Circuits and Syst-I,2006,53(2):384-393.
[7]XIANG Zhengrong,WANG Ronghao.Robust stabilization of discrete-time switched non-linear systems with time delay under asynchronous switching[J].Trans Inst Measur Contr,2011,33(5):591-609.
[8]MONDIE S E,KHARITONOV V L.Exponential estimates for retarded time-delay systems:an LMI approach[J].IEEE Trans on Autom Contr,2005,50(2):268-273.
[9]LIEN C H,YU K W,LIN Y F,et al.Global exponential stability for uncertain delayed neural networks of neutral type with mixed time-delays[J].IEEE Trans Syst Man Cybern B,2008,38(3):709-720.
[10]SUN Yuangong,WANG Long,XIE Guangming.Delay-dependent robust stability andH∞control for uncertain discrete-time switched systems with mode-dependent time delays[J].Appl Math Comput,2007,187(2):1228-1237.
[11]ZHANG Wei,CAI Xiushan,HAN Zhengzhi.Robust stability criteria for systems with interval time-varying delay and nonlinear perturbations[J].J Comput Appl Math,2010,234(1):174-180.
[12]ZHA Guisheng,SUN Ye,CHEN Xinkai,et al.Stability and L2gain analysis for switched symmetric systems with time-delay[C]∥Am Contr Conf,2003:2682-2687.
[13]SUN Ximing,WANG Feng,LIU Guoping,et al.Stability analysis for linear switched systems with time-varying delay[J].IEEE Trans Syst Man Cybern B,2008,38(2):528 -533.
[14]HIEN L V,HA Q P,PHAT V N.Stability and stabilization of switched linear dynamic systems with time delay and uncertainties[J].Appl Math Comput,2009,210(1):223-231.
[15]ZHANG Xiaoli.Analysis of robust stability for switched systems with multiple time-delays[J].Contr Theor Appl,2011,9(2):283-288.
[16]WANG Limin,SHAO Cheng.Robust stability analysis of switched uncertain systems with multiple time-varying delays and actuator failures[J].Contr Theor Appl,2011,9(2):267-272.
[17]ZAIRONG Xi,GANG Feng.A switching algorithm for global expopnential stabilization of uncertain chained systems[J].IEEE Trans on Autom Contr,2003,48(10):1793-1798.

