淺談數學思想在小學數學教學中的滲透

謝文彪

【摘要】小學數學教學中數學思想的滲透是學生終生受益和發展的要求，教師要深研教材，不斷學習，研討與實踐，通過備課、上課、作業設計等環節加以滲透數學思想，使學生逐步學會運用數學思想方法分析與解決問題，從而發展學生的數學素養。

【關鍵詞】數學思想 滲透 培養

【中圖分類號】G623.5 【文獻標識碼】A 【文章編號】2095-3089（2013）05-0154-02

《小學數學新課程標準》中指出：“讓學生能夠獲得適應社會生活和進一步發展所必須的數學的基本知識、基本技能、基本思想、基本活動經驗”。新課標從“兩基”擴展到“四基”，它倡導人人學有用的數學，不同的人在數學上得到不同的發展。更加關注學生的個體差異、個體發展需求、個體發展空間，強調使人受用一生的數學思想的重要性。

數學思想是對數學本質的認識，是現實世界的空間形式和數量關系反映到人們的意識之中，經過思維活動而產生的結果。數學思想是數學知識的精髓，是知識轉化為能力的橋梁，是數學課程的重要目標，數學思想貫穿于數學的學習過程，與數學知識是相互交融的，密不可分的。相比較而言，許多具體的數學知識學過之后是可以忘掉的，而那些知識所表現的數學思想的有效性卻是長期的，對人的學習、工作、生活、社會實踐具有普遍的指導意義，學會用數學的眼光看世界，學會數學的思維，更有利于學生形成科學的思維方式和思維習慣，受益終生。作為教師，在教學實踐中，如何滲透數學思想，充分體現新課程理念呢？下面以本人在人教版六年級下冊第91頁《數學思考》教學實踐為例，談談自己的體會和膚淺看法。

一、研讀教材，明確目標，挖掘數學思想方法，備好課。

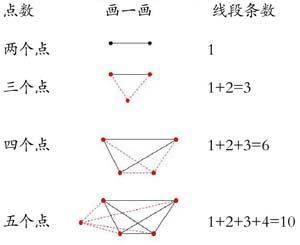
小學數學教材中蘊含著數形結合、集合、對應、函數、化歸、極限、分類、符號化、數學建模、統計、假設、代換、比較、可逆等數學思想方法。但是由于教材篇幅的限制，并沒有注明隱含的數學思想方法和數學思維活動的過程。沒有說明什么內容將和中學或高等數學內容銜接。這就需要教師進一步鉆研教材，創造性地使用教材，挖掘隱含在教材中的數學思想，并在教學目標中明確寫出滲透哪些數學思想方法，并設計數學活動落實在教學預設的各個環節中，實現數學思想方法有機的融合在數學知識的形成過程中。使教材呈現的知識技能這條明線與隱含的思想方法的暗線同時延展，做到胸有成竹，有的放矢。例如在備六年級下冊《數學思考》一課中，教材呈現的例5、六個點可以連成多少條線段？8個點呢？（如圖），通過學生動手例舉，從2個點開始，逐漸增加點數，找規律就有：

2個點連成一條線段：1（條）

3個點連成線段的條數：1+2=3（條）

4個點連成線段的條數：1+2+3=6（條）

5個點連成線段的條數：1+2+3+4=10（條）

6個點連成線段的條數：1+2+……+5=

8個點連成線段的條數：1+2+……+6+7=

從教材所呈現的內容，找到規律：6個點連成的線段就是從1加到5的和，8個點連成的線段就是從1加到7的和。但是，我們在備課時還不能僅限于此，必須將教材內容作深度思考和拓展，為此，提出兩個問題：

1.如果有n個點，它連成的線段應該有多少條？

學生通過類比、歸納是可以得到這樣的結論：n個。

點連成的條數是從1加到（n-1）的和。這里應用了類比、歸納、符號化、數學建模等數學思想方法。

2.8個點連成的線段條數是1+2+3+……+7=（ ），你怎樣求和？n個點連成的線段條數又怎樣算呢？

我的教學預設是通過學生已經熟知的數學家高斯的故事。

1+2+3+……+99=100=（1+100）×100÷2=5050

學生通過思考，應用代換、化歸、符號化、數學建模等數學思想方法得到等差數列求和的一般方法：

（首項+末項）×項數÷2

從而推導出：

8個點連成線段的條數是1+2+3+……+7=（1+7）×7÷2=28（條）

n個點連成線段的條數是1+2+3+……+（n-1）=（1+n-1） × （n-1） ÷2=n×（n-1） ÷2

最終得出n點連成線段的條數為：n×（n-1） ÷2

學生通過上述的探究活動，已經涉及到了“等差數列及等差數列求和”這一高中數學知識內容，為今后進一步深入學習作基礎性鋪墊。通過探究活動，把具有一定規律的事物和現象，應用歸納、代換、演繹、符號化、數學建模等數學思想方法進行簡單抽象的公式化描述，感知和體會數學思想方法的魅力和奧妙，培養學生的數學素養，激發學生學習數學的興趣。

另外，本課時教學內容，如果從理論出發，還可以向學生提出一個思考性的問題——有n個點，兩點為一組，有幾組？

我們知道，一條線段有兩個端點，如果有n個點，那么從這n個點中任意的兩個點為一個組合，就能夠連成一條線段。也就是說，n個點中有幾個這樣的組合，就能連成幾條線段，這又涉及到高中的數學知識（排列與組合），上面的問題可以用一個簡單的數學符號（Cn2）來表示，向學生進行簡短的說明，從而激發學生的求知欲。

二、創設情境、建立模型、解釋應用、滲透數學思想方法、上好課。

數學知識與思想方法是有機的結合體，數學知識發生、形成、發展的過程也是其思想產生、應用的過程。所以，我們的課堂，既要讓學生獲得數學知識的同時，又要讓學生獲得數學思想方法的點化。對于小學生來說，由于年齡特征和認知規律所決定，應向學生提供豐富的、典型的、正確的直觀背景材料，并努力讓學生動手、動腦、活動、參與、探究學習數學知識，從而感受和領略數學思想方法。比如在讓學生尋找點數與線段之間的規律時，在教學中，讓學生動手畫一畫，算一算，如下：

點數 畫一畫 線段條數

兩個點 1

三個點 1+2=3

四個點 1+2+3=6

五個點 1+2+3+4=10

問：6個點呢？讓學生觀察、思考找出規律，并說一說你是怎樣想的？

生1：五個點有10條線段，增加一個點，就與另外5個點分別連成5條線段，6個點就是10+5=15（條）。

生2： 六個點就是1+2+3+4+5=15（條）。

生3：六個點就是從1加到5的和。

師問：8個點呢？n個點呢？

通過學生動手、動腦主動探索，滲透并應用數形結合、對應、有序思考、分類歸納等數學思想方法，最終找出n個點連成線段的條數：從1加到（n-1）的和。

三、精心設計、有效練習、恰當點評、應用數學思想方法。

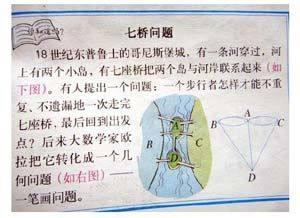
精心設計數學作業也是滲透數學思想的一條重要途徑，把作業設計好，設計一些蘊含數學思想方法的題目，采取有效的練習方式，既鞏固了知識技能，又有機的滲透了數學思想方法，一舉兩得。在學生作業后，要不失時機的給予恰當點評，讓學生不僅鞏固所學知識，學得解題技能，更重要的是能悟出其中的數學規律、數學思想。再如六年級數學下冊練習十八中的“你知道嗎”——七橋問題，（如圖）教師在點評該思考題要 指出兩點：

1.數學家歐拉把它轉換成一個幾何問題，是把一個實際問題抽象成恰當的“數學模型”，體現了解決數學問題的一種基本思想方法——數學建模方法。

2.引導學生思維的求異性。一般地，有問題，就有答案，而七橋問題轉化成一個幾何圖形，就成為了“一筆畫”問題，要一筆畫玩并不重復回到起點，必須是經過所有點的線都為偶數才行。形象簡單地說，從起點出發再回到起點，應有兩條線為偶數，若是奇數線，就只能是走得出去，回來不了，七橋問題的四個點都為奇數線。所以要一次不重復、不遺漏地走完七座橋是不可能的，沒有正確答案，無解。

通過引發學生思考和講評，讓學生感受數學建模、數形結合、類比推理等數學思想方法、體會數學思想的巨大威力。

總之，在小學數學教學中要通過不斷學習、鉆研教材、備好課；積極研討與實踐、上好課；精心設計作業、恰當點評；指導和組織學生課外活動等環節，不失時機地滲透數學思想方法，逐步培養學生的數學興趣和素養，讓學生學會用數學的眼光看世界，用數學思想方法解決處理實際問題；讓學生形成科學的思維方式和思維習慣，參與社會實踐；讓學生今后科學地、有效地、正確地從事各種工作，服務于人民，服務于社會，服務于人類，受益終生。