基于烏魯木齊物流產業分析多重共線性

李育冬，吳 昊，夏蘇清

（1新疆大學 經濟與管理學院，新疆 烏魯木齊830046；2解放軍69081部隊，新疆 烏魯木齊830000）

在經濟學構建回歸模型分析時，經典的簡單最小二乘估計（OLS），必須滿足高斯假設等苛刻的假設條件，而在實際分析經濟學問題的時候，解釋變量之間完全不相關的情形是十分少見的，由于經濟學分析的社會問題往往涉及面廣泛，考察的自變量多，當研究時間序列數據時候，大多數自變量隨著時間變化往往存在共同的變化趨勢，使得它們之間在某種程度上存在著一定的共線性；而對于截面數據常常也存在自變量高度自相關的情況，而存在著共線性會給模型帶來許多不確定性的結果。

一、多重共線性的認識

（一）多重共線性的定義

設回歸模型y＝β0＋β1x1＋β2x2＋…＋βpxp＋ε如果矩陣X的列向量存在一組不全為零的p＋1個數k0，k1，k2…kp使得k0＋k1xi1＋k2xi2＋…＋kpxip＝0，i＝1，2，…n，則稱其存在完全共線性，如果k0＋k1xi1＋k2xi2＋…＋kpxip≈0，i＝1，2，…n，則稱其存在多重共線性，也稱復共線性。

（二）多重共線性的后果

多重共線性其實是由樣本容量太小所造成的后果，當樣本容量n很小的時候，多重共線性才是非常嚴重的。在不同口徑下有關的許多變量，變量太多不但會增加計算的復雜性，而且也給全面合理地分析問題和解決問題帶來很大困難，雖然每個變量都提供了一定的信息，但每個變量的重要性有所不同。當存在多重共線性時，自變量用來解釋因變量所提供的信息出現重疊，多重共線性導致模型回歸系數參數估計的標準誤差變大，置信區間變寬，利用OLS估計得到的回歸參數估計值很不穩定，回歸系數的方差隨著隨著多重共線性強度的增加而加速增長，常常會出現在回歸方程高度顯著的情況之下，有些回歸系數通不過顯著性檢驗，還常常會出現回歸系數正負號得不到合理的經濟學解釋。因此，在經濟學研究之中構建多元回歸模型考察因變量時要消除多重共線性的影響。［1］180-183

多重共線性的常見影響有：

（1）在存在多重共線性的情況下，得到的OLS估計結果是最優線性無偏估計的，但有較大的方差和協方差，估計精度不高，最突出的就是參數估計值的方差增大；

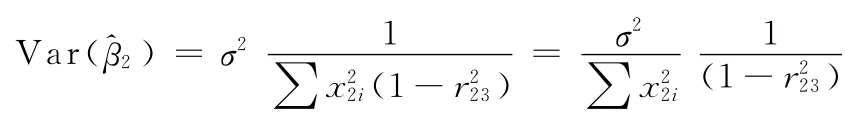
當r23增大時，Var（）也增大。

（2）對參數區間估計時，置信區間趨于變大，使得接受原假設H0的概率更大；

（3）假設檢驗容易作出錯誤的判斷；

（4）可能造成擬合優度R2較高，但對各個參數單獨的t檢驗卻可能不顯著，甚至可能使估計的回歸系數符號相反，得出完全錯誤的結論，得不出合理的經濟學解釋。

（5）OLS估計量及其標準誤對數據微小的變化也會很敏感。

（三）多重共線性產生的原因

（1）經濟變量之間具有共同變化趨勢。由于考察的自變量隨時間變化往往有共同的變化趨勢，往往受到共同因素的影響，各個自變量之間存在著共線性。例如當經濟出現大繁榮時，反映經濟情況的指標都有可能按著某種比例關系增長。

（2）模型中包含滯后變量。滯后變量的引入也會產生多重共線行，例如本期的消費水平除了受本期的收因素入影響之外，還有可能受前期的收入因素影響，建立模型時，本期的收入水平就有可能和前期的收入水平存在著共線性。

（3）利用截面數據建立模型也可能出現多重共線性。在經濟學研究建立多元回歸模型時利用的截面數據本身就有可能存在自相關性，如果沒有進行處理建立的模型就有可能存在著共線性。

（4）樣本數據采集方法的原因。

（四）多重共線性的識別

1.簡單觀察法

（1）在自變量的相關系數矩陣中，一些自變量的相關系數值比較大；

（2）回歸系數的符號與經濟學常識相反或者難以解釋；

（3）重要考察的自變量的置信區間過大；

（4）如果增加一個變量或刪除一個變量，回歸系數的估計值發生了很大的變化；

（5）對重要的自變量的回歸系數進行t檢驗，其結果不顯著，但是F檢驗確得到了顯著的通過。

2.方差擴大因子法（VIF）

3.特征根判定法

由于矩陣行列式的值等于其特征根的連乘積，因此當行列式｜X′X｜≈0時，至少有一個特征根為零，反過來，可以證明矩陣至少有一個特征根近似為零時，X的列向量必存在多重共線性，同樣也可證明X′X有多少個特征根近似為零矩陣，X就有多少個多重共線性。根據條件數其中λ為最大的特征根，λ為其mi他的特征根，通常認為0＜K＜10，沒有多重共線性，100＞K＞10存在著一般多重共線性，K＞100存在著嚴重多重共線性。

（五）多重共線性的處理方法

1.增加樣本容量

當多重共線性出現是由于測量誤差引起的，而不存在于總體樣本時，通過增加樣本容量可以減少或是避免線性重合，但是在現實的生活中，由于受到各種統計數據不足的限制，增加樣本容量有時又是不現實的。

2.剔除法

當面當面臨嚴重的共線性時，一種最簡單的方法就是剔除掉一些不太重要的自變量，主要有向前法和后退法，逐步回歸法。但決定保留或剔除哪些自變量并不是一件容易的事。因此，如何判斷某個變量是否重要，是此方法的關鍵。從模型中刪除一個變量，還可能導致設定偏誤。此外，在一些經濟模型中，要求一些很重要變量必須包含在里面，這時如果貿然的刪除就不符合現實的經濟意義。

3.主成分分析法

主成分分析一種處理嚴重共線性的有偏估計方法。當自變量間有較強的線性相關性時，利用p個變量的主成分，所具有的性質，如果他們是互不相關的，可由前m個主成Z1，Z2，…Zm來建立回歸模型。

由原始變量的觀測數據計算前m個主成分的得分值，將其作為主成分的觀測值，建立Y與主成分的回歸模型即得回歸方程。這時p元降為m元，這樣既簡化了回歸方程的結構，且消除了變量間相關性帶來的影響。然而，主成分估計提取的主成分與因變量關系也不密切，使模型的擬合效果降低；而且以此同時主成分的實際含義也不明確。［2-3］

4.偏最小二乘法（PLS）

PLS法是由H.Wold在1966年提出的PLS是由Wold（1966）提出的，PLS≈主成分估計＋典型相關分析。PLS吸取了主成分估計的思想，提取的主成分考慮了對因變量的解釋能力，使估計值優于主成分估計值。可是，與此同時PLS也繼承了主成分估計的一些缺點，如主成分含義也不明確、信息重疊等現象。

5.嶺回歸法

嶺回歸分析是由Heer首先提出的，他與肯納德合作，進一步發展了該方法，在多元線性回歸模型的矩陣形式Y＝Xβ＋ε，參數β的普通最小二乘估計為β＝（X′X）-1X′Y，嶺回歸當自變量存在多重共線性｜X′X｜≈0時，給矩陣加上一個正常系數矩陣kI，那么β＝（X′X＋kI）-1X′Y，當時就是普通最小二乘估計。嶺回歸也是有偏估計方法。當出現嚴重共線性時，嶺估計往往比OLS估計量更穩定，以及更小的協方差矩陣。嶺估計的最大困難是最優k值的選擇。盡管人們提出了許多確定k值的原則和方法，但理論上還未得到滿意答案。此外，在實際應用中k值必須通過樣本來確定，存在明顯的主觀性。［4］

二、處理多重共線性的實際運用

根據烏魯木齊市統計年鑒［5］，選取烏魯木齊市2000年至2012年的物流產業相關統計數據做一個多元回歸模型，選取烏魯木齊市的貨運量周轉量（Y）為因變量，進出口總額（X1）、社會消費品零售總額（X2）、物流業就業人數（X3）、公路里程（X4）、郵電業務收入（X5）5個變量為自變量，將所有變量加以對數化處理。構建多元回歸模型為LNY＝β1LNX1＋β2LNX2＋β3LNX3＋β4LNX4＋β5LNX5＋ε……（3.1）；其中ε為隨機干擾項。

1.簡單最小二乘估計法

運用SPSS統計軟件進行分析，從簡單二乘法估計結果可以看到，調整的擬合優度R2＝1，F＝34880.71，在置信水平為95%，自由度4，方程通過了顯著性的檢驗，從整體上來說方程得到了很好的擬合，通過篩選方程剔除了自變量LNX2，同時變量LNX1，LNX3不顯著，LNX1系數為負，和經濟學的原理相反。方差擴大因子VIF1＝2649.482，VIF2＝659.07917，VIF3＝1463.4738，VIF4＝1585.8618.均大于10說明存在多重共線性。再由多重共線性診斷結果可以看到，特征值有兩個接近于零，最大條件數為120.408，且直觀可以看出，第四個特征值的方差既可以解釋LNX1方差的98%，也可以解釋LNX3方差的86%，說明自變量間存在著嚴重的多重共線性。

2.運用嶺回歸解決多重共線性

用SPSS軟件采用嶺回歸法做出的結果如下：

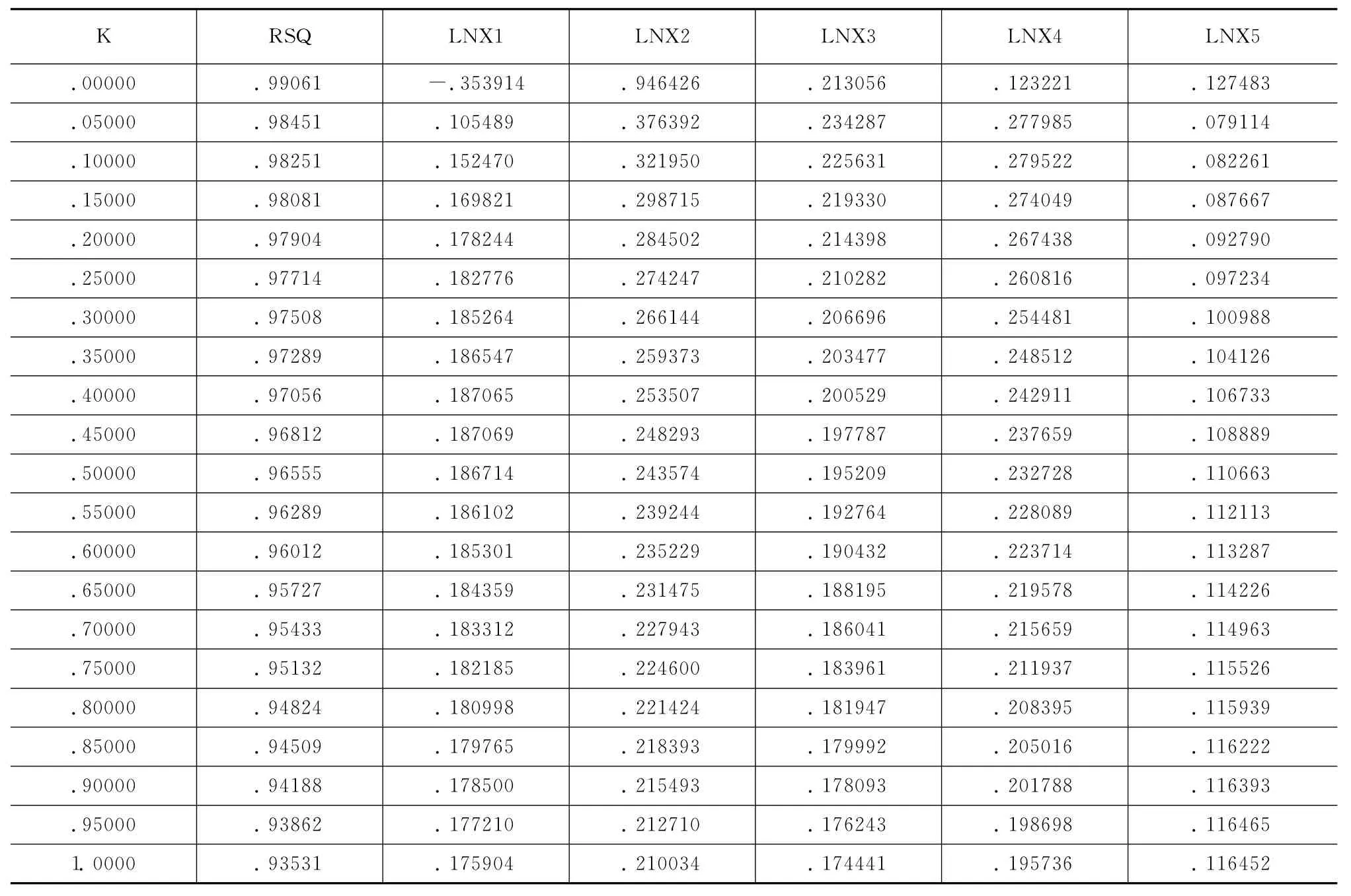
表1 嶺參數K值表

從嶺跡圖上看，最小二乘的穩定性很差，當K稍微增大時，系數有較大的變化。對各個變量分別來看，當K＝0，LNX2、LNX3、LNX4、LNX5對于變量有顯著性正的影響，LNX1對于變量有負的影響，從嶺回歸的角度來看，自變量LNX2，LNX3，LNX4隨 K的增大其系數值迅速減小最終趨于穩定，LNX1隨K的增大其系數值迅速增加最終趨于穩定，當K逐漸增大時，LNX1由負的影響迅速變為正的影響并且趨向于穩定，由此決定用5個變量做嶺回歸。把嶺參數步長改為0.02，范圍縮小到0.2，在SPSS中用命令生成得到如下結果：

表2 調嶺參數步長＝0.02后嶺參數K值表

從嶺參數K值表結果看，當嶺參數K在0.06-0.10之間已經基本穩定，當K＝0.08時候，R2＝0.98322仍然很大，因而可以選取嶺參數K＝0.08，給定K＝0.08再次做嶺回歸，得到輸出結果如表3所示。

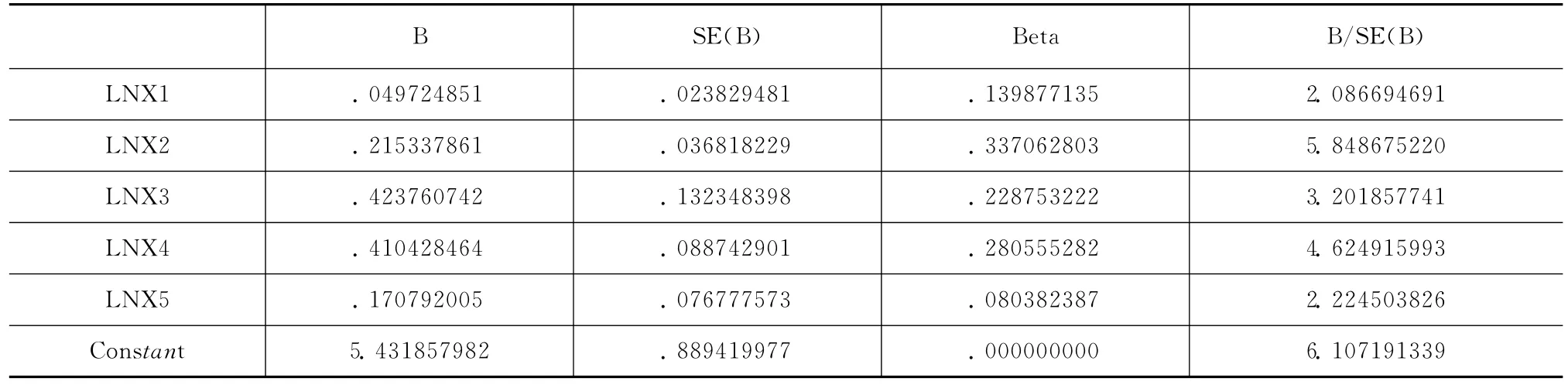
表3 K＝0.08時嶺回歸輸出結果

由嶺回歸輸出結果可以得到LNY對于LNX1，LNX2，LNX3，LNX4，LNX5標準化嶺回歸方程為：

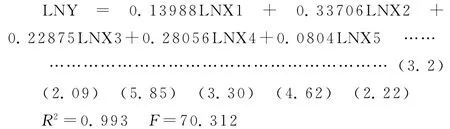
由此我們可以看出，通過標準化嶺回歸得到的T統計量比OLS估計顯著，各個變量的系數經濟意義也更加合理，可以看到各個變量對烏魯木齊貨運量不同程度的影響。

3.主成分分析法

用SPSS軟件采用主成分分析法可以得到前兩個因子的累積貢獻率已經達到91%以上，故取因子數m＝2。提取出公共因子，為了使因子便于解釋，使用方差極大法將因子旋轉，采用回歸法估計因子得分系數，得出函數如下：

進而可以得出，

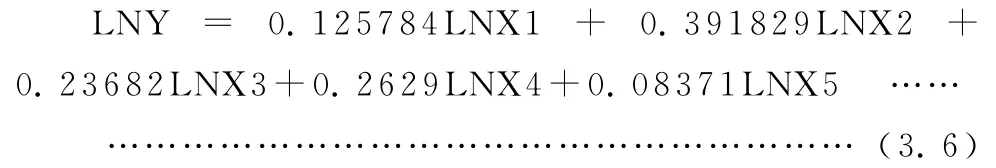
由上面的分析我們看到嶺回歸和主成分的所得到的結果比較接近，得出的各個系數比較簡單二乘法也更加的合理，更加符合現實意義。

三、結 論

主成分分析法和嶺回歸法所估計的參數，都已經不是無偏的估計，主成分分析法作為多元統計分析的一種常用方法在處理多變量問題時具有其一定的優越性，其降維的優勢是明顯的，主成分回歸方法對于一般的多重共線性問題還是適用的，尤其是對共線性較強的變量之間.嶺回歸法估計是通過最小二乘法的改進允許回歸系數的有偏估計量存在而補救多重共線性的方法，采用它可以通過允許小的誤差而換取高于無偏估計量的精度，因此它接近真實值的可能性較大，但k值的選取具有主觀性，選取不當可能造成很大誤差。作為統計方法，每種方法都有其適用范圍，沒有一種統計方法具有超過其他方法的特殊優勢，在實際計量統計分析需要依據考察因變量、自變量的特點和數據特征靈活加以運用。

［1］何曉群.應用回歸分析［M］.北京：中國人民大學出版社，2007.

［2］白雪梅，趙松山.更深入地認識多重共線性［J］.東北財經大學學報，2005（2）：8-12.

［3］劉羅曼.用主成分回歸分析解決回歸模型中復共線性問題［J］.沈陽師范大學學報：自然科學版，2008（1）：42-44.

［4］劉國旗.多重共線性的產生原因及其診斷處理［J］.合肥工業大學學報：自然科學版，2001（4）：607-610.

［5］烏魯木齊統計局.烏魯木齊統計年鑒2012［M］.北京：中國統計出版社，2012.