基于小波神經網絡的空氣污染指數預報

李四海，魏邦龍，李愛英

(1.甘肅中醫學院 公共課部，蘭州 730000;2.蘭州城市學院 信息工程學院，蘭州 730070;3.蘭州市經濟管理干部學校，蘭州 730083)

0 引言

大氣污染物濃度的變化主要受同期氣象條件的影響，研究氣象條件與大氣污染之間的關系對于大氣質量預報及控制具有重要作用。近年來，小波分析及BP神經網絡被廣泛應用于氣象因子與污染物濃度之間的非線性建模。小波分析用于對空氣污染指數和大氣污染物濃度時間序列進行多尺度分解，以發現序列的趨勢性及局部波動性和隨機性［1］。BP神經網絡則用于建立氣象因子與大氣污染物SO2、NOx、可吸入顆粒物PM10等之間的非線性映射［2-3］，但是單純以氣象因子作為網絡輸入，基于BP預報空氣污染指數時，在時間序列非平穩段的預測精度不高且網絡的收斂速度慢。

該文結合小波分析的多分辨率性質和人工神經網絡的自學習、非線性逼近能力，提出了一種新的空氣污染指數預報模型，小波神經網絡模型(Wavelet Neural Network)。該模型應用小波的特征提取能力，提取時間序列在不同系列小波焦距下的高低頻信息。以各尺度上的小波系數序列和重要的氣象因子為輸入，對蘭州地區的空氣污染指數進行實例預報，結果表明模型具有較高的預測精度，用于空氣污染指數預報具有可行性和有效性。

1 影響空氣污染指數的氣象因子

研究表明［4］，靜風、逆溫是構成蘭州大氣污染的基礎原因，由于靜風、逆溫頻率高，造成大氣的穩定度高，這又進一步加劇了該市冬季的大氣污染。

空氣污染指數通常是根據SO2、NO2、PM10的濃度計算得出，根據計算結果的不同將空氣質量分為優、良、輕度污染、中度污染、重度污染五個級別。研究表明，這三種污染物濃度與平均風速、平均溫度呈負相關，與相對濕度呈正相關［5］。

根據以上分析，以最高溫度、最低溫度、平均風速及相對濕度作為小波神經網絡的第一組輸入。

2 小波神經網絡預報模型

2.1 離散小波變換

小波分析是一種非平穩信號分析方法，通過一個基本小波的伸縮和平移構成一系列小波函數用于對信號進行多尺度逼近和分析。小波變換具有良好的時頻局部化能力，能夠將信號分解為任意系列頻帶的直和，享有信號處理的“數學顯微鏡”美譽。

設信號f(t)在Vj空間中的離散采樣序列為f(k)，k=0，1，2，…，n-1，則Mallat小波分解算法為:

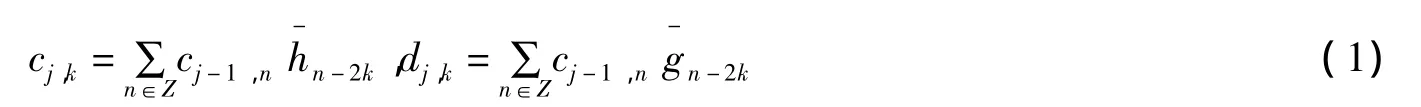
其中cj，k和dj，k分別為信號的低頻和高頻部分，h(n)和g(n)分別為低通濾波器H和高通濾波器G的系數，且gn=(-1)nh1-n

Mallat重構算法為:

2.2 小波神經網絡預報模型

2.2.1 小波特征提取

小波具有許多良好的性質，如消失矩、正交性等，小波變換常用于去噪、壓縮及特征提取。該文選用db3小波，使用Matlab7.1中的小波工具箱對2011.4.21-2012.4.20的空氣污染指數序列進行三層小波分解，對各層高低頻系數使用wrcoef函數進行單支重構，得到原始序列的小波分解序列{a3，d3，d2，d1}，其中a3為低頻子序列，是原始序列的近似，反映了原始序列的長期變化趨勢;d3，d2，d1是高頻子序列，是原始序列的細節，反映了原始序列在不同“焦距”下的隨機性和波動性。小波分解的結果如圖1所示:

圖1 原始時間序列的小波分解

2.2.2 網絡結構

小波神經網絡綜合了小波變換的分辨率性質和神經網絡的自學習能力，在處理非線性問題時表現優異，已廣泛用于各個領域［6-7］。

小波神經網絡主要有兩種結構:松散型和緊湊型。松散型不改變網絡的結構，首先利用小波對信號進行多層分解，然后將分解得到的小波系數序列交由神經網絡處理，特別適用于非平穩信號的預測與分析。緊湊型結構則以小波基函數作為隱層單元的激勵函數，常用的小波基函數為Morlet函數，本研究采用松散型結構，網絡分為輸入層、隱層和輸出層。

取2011.4.21 日 -2012.4.20 日氣象數據中的最高溫度、最低溫度、平均風速、相對濕度、前一日空氣污染指數及小波單支重構序列{a3，d3，d2，d1}作為網絡的最終輸入，共9個輸入，輸出為空氣污染指數。網絡結構如圖2所示:

3 網絡訓練和仿真

以2011.4.21-2012.4.20 的數據作為訓練樣本，將數據按維度歸一化至［-1，1］。隱層單元范圍由經驗公式確定［15］，假設n1，n2分別為輸入層和輸出層單元數，n為隱層單元數，則最佳隱層單元的范圍為:［log2n1，+［1，10］］，在此范圍內經過多次實驗，比較訓練誤差和測試誤差，最終取n=13。因此，網絡結構為9-13-1。隱層和輸出層轉移函數分別為tan-sig、purelin，采用 traingdx 算法訓練網絡，訓練精度0.001，lr=0.015。

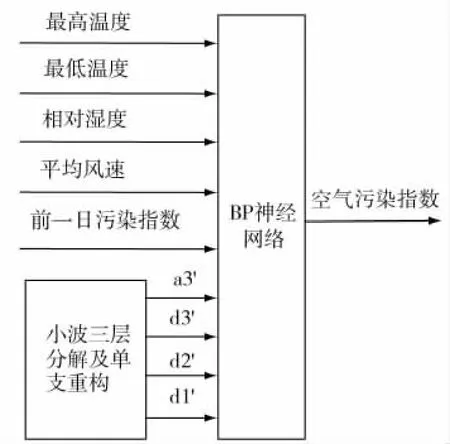
圖2 小波神經網絡結構圖

將2012.4.21日-2012.6.17日的58個樣本作為測試樣本，使用WNN模型進行測試，當訓練步數達到2303步時網絡收斂，其誤差平方曲線如圖3所示。

僅以四個氣象因子和前一日的空氣污染指數作為BP網絡輸入對相同的樣本進行測試，兩種模型的測試結果如表1所示。

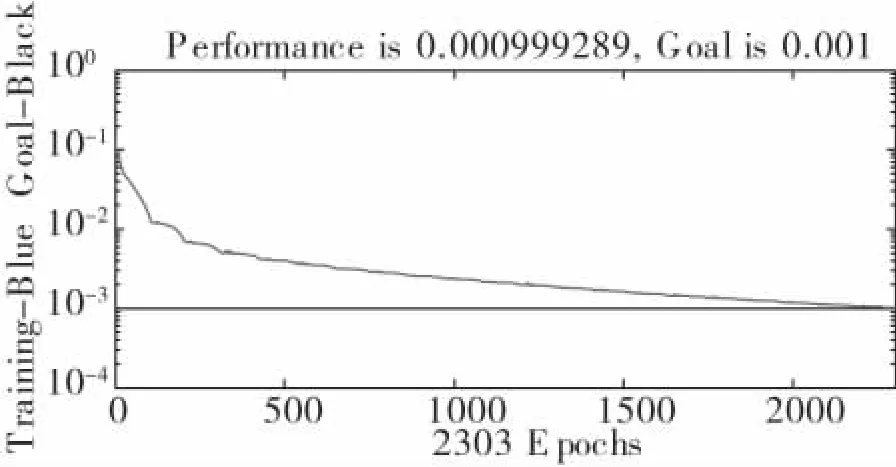
圖3 誤差平方曲線

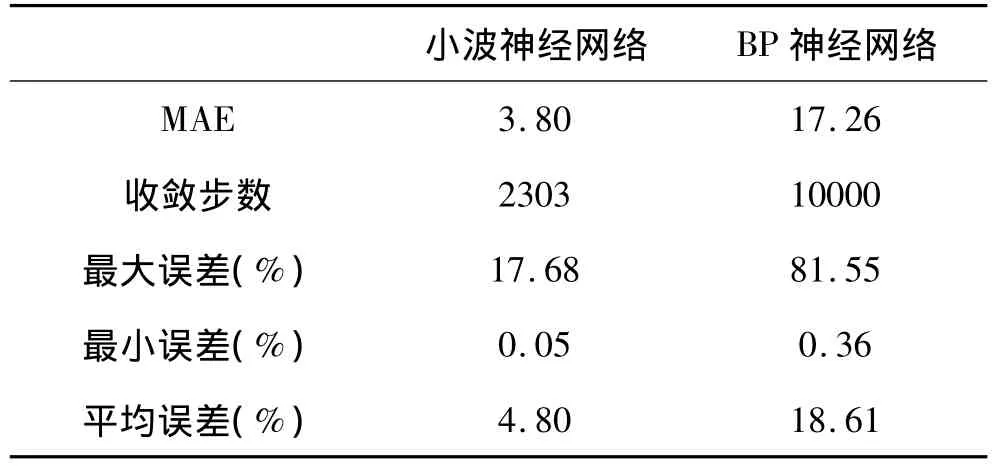
表1 小波神經網絡和BP網絡仿真結果對比

從仿真實驗的結果可知，兩種模型都能反映出空氣污染指數序列的總體變化趨勢。從收斂速度來看，BP網絡在訓練精度為0.01時，到達預設的10000步才收斂，收斂速度慢。比較兩者的預測精度，BP神經網絡在時間序列的平穩階段預測精度較好，但在時間序列波動較大的階段，預測精度較差，部分原因在于訓練樣本較少導致欠學習，模型泛化能力不高，更重要的原因在于有限樣本中包含的信息量少，輸入中沒有時間序列本身的趨勢性及波動性信息。小波神經網絡由于對原始序列進行了小波分解，其低頻序列能夠表現空氣污染指數序列的趨勢性，各尺度上的高頻子序列則反映了空氣污染指數序列的隨機性和波動性。這種多尺度分析能夠以任意精度“聚焦”原始序列在任意細節上的差異性，有利于提前預判序列的變化趨勢及局部的波動性，從而提高網絡的預測精度，特別當時間序列局部波動性較大時，效果更為明顯，充分顯示了小波神經網絡模型較強的魯棒性。表1對比了兩種模型的收斂速度及預測精度，其中MAE為平均絕對誤差。

從表1可以看出，與BP神經網絡相比，小波神經網絡具有更好的預測精度，更快的收斂速度以及較好的自適應性。

4 結語

BP神經網絡預測空氣污染指數時收斂速度慢、泛化能力較差，提出了小波神經網絡預測模型，研究了網絡模型的結構及參數對網絡性能的影響。對空氣污染指數的仿真結果表明該模型對序列的平穩和非平穩階段均具有較高的預測精度和魯棒性，是一種行之有效的空氣污染指數預報方法。基于各種智能算法自適應調節權重參數和學習率，進一步提高小波神經網絡的預測精度、收斂速度及泛化能力將是下一步的研究方向。

［1］ 王海鵬，等.基于小波變換的蘭州市近十年空氣污染指數變化［J］.環境科學學報，2011，31(5):1071-1076.

［2］ 張靜，李旭祥，許先意，等.大氣環境數據分析預測方法對比研究［J］.中國環境監測，2010，26(6):66-70.

［3］ 王芳，程水源，李明君，等.遺傳算法優化神經網絡用于大氣污染預報［J］.北京工業大學學報，2009，35(9):1230-1234.

［4］ 高建華.蘭州市大氣污染規律及治理對策［J］.西安石油學院學報:自然科學版，2003，18(4):85-88.

［5］ 周秀杰，蘇小紅，袁美英.基于BP網絡的空氣污染指數預報研究［J］.哈爾濱工業大學學報，2004，36(5):582-585.

［6］ 張坤，郁湧，李彤.小波神經網絡在黃金價格預測中的應用［J］.計算機工程與應用，2010，46(27):224-241.

［7］ 楊艷，李靖，馬顯瑩，等.基于小波神經網絡的城市用水量長期預測研究［J］.云南農業大學學報，2010，25(2):272-276.

［8］ 沈花玉，王兆霞，高成耀，等.BP神經網絡隱含層單元數的確定［J］.天津理工大學學報，2008，24(5):13-15.