雙軸旋轉慣導系統的轉位方案優化技術研究*

朱 蕾，袁書明，程建華

(1.海軍裝備研究院艦船所，北京100073;2.哈爾濱工程大學自動化學院，黑龍江哈爾濱150001)

0 引言

旋轉調制捷聯慣導系統通過旋轉機構的引入，實現了慣性器件誤差的有效調制，大大提高了捷聯式慣導系統的導航定位精度，在國內外高精度艦船導航領域得到了大量的應用，如美國SPERRY公司的MK39單軸旋轉捷聯慣導和 MK49 雙軸旋轉捷聯慣導系統［1～3］。

單軸旋轉方式由旋轉機構提供一個轉軸用于慣性器件誤差的調制，這種方案結構簡單、易實現、成本低，目前仍是應用較為廣泛的旋轉調制方案。但由于單軸旋轉方案無法實現三軸器件誤差調制，因此，未從根本上解決慣導系統定位誤差隨時間積累的問題。而雙軸旋轉捷聯慣導由于能夠調制三軸慣性器件誤差，因此，具備了從根本上抑制慣導系統誤差隨積累的特性［4］。

轉位方案是影響旋轉調制效果的重要因素，一直是國內外學者在旋轉式捷聯慣導系統方案設計的重要研究內容。不僅如此，在同類轉位方案中，轉位方式、轉位次序和轉位速率的不同，也會產生不同的調制效果。

雙軸依次旋轉調制方案是目前國內外學者最多采用和研究的一種方案，但在方案研究和設計過程中，多數文獻僅分析旋轉方案對器件誤差的調制效果，未從定量角度分析轉位方案的細節參數對系統定位性能的影響［5，6］。

基于此，本文就雙軸依次旋轉捷聯慣導系統方案，就轉位過程中的旋轉、停止時間對定位性能影響開展研究，通過對定位性能的分析改進轉位方案，達到提高捷聯慣導系統精度的目的。

1 雙軸依次旋轉的誤差調制效果分析

1.1 雙軸依次旋轉慣導原理

陀螺儀和加速度計是慣性導航系統的2個核心慣性器件，二者的精度決定了慣性導航系統的位置、速度和姿態精度。而從頻域角度分析慣性導航系統特性可知，慣導系統具有對高頻干擾衰減的特性，即具有較高頻率的周期干擾作用在低通特性的系統上，漂移造成的誤差將大為減小，旋轉式慣導系統正是利用了這一特性，將常值誤差調制為高頻誤差，提高系統精度。

雙軸依次旋轉慣導系統通過引入具有2個旋轉自由度的旋轉機構進行慣性元件誤差調制，常用的八位置雙軸依次旋轉方案如圖1所示［7］。

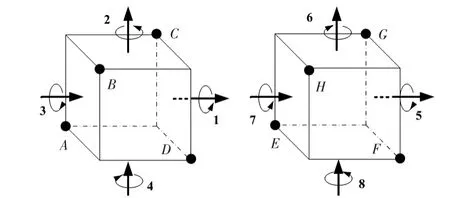
圖1 雙軸依次旋轉效果圖Fig 1 Effect diagram of double-axis rotation sequences

圖1中，箭頭指向代表旋轉軸指向，各旋轉次序的旋轉時間為tr，在各位置的停止時間為ts。

依據圖1可得八位置雙軸依次旋轉慣導系統的轉動次序為:

次序1:繞東向軸正轉180°由A到位置B停止;

次序2:繞天向軸正轉180°由B到位置C停止;

次序3:繞東向軸反轉180°由C到位置D停止;

次序4:繞天向軸反轉180°由D到位置A停止;

次序5:繞天向軸正轉180°由E到位置F停止;

次序6:繞東向軸反轉180°由F到位置G停止;

次序7:繞天向軸正轉180°由G到位置H停止;

次序8:繞東向軸正轉180°由H到位置E停止。

1.2 漂移調制效果分析

為簡化問題分析，設初始時刻，框架坐標系oxryrzr、載體坐標系oxbybzb和地理坐標系oxtytzt重合，由此可計算出8個轉動次序過程中的陀螺等效漂移為

依據旋轉次序、變換矩陣Tbr和式(1)，可以求得沿地理系的等效漂移如圖2～圖4中實線所示。

圖2 等效東向陀螺漂移Fig 2 Drift curve of the equivalent east gyro

圖3 等效北向陀螺漂移Fig 3 Drift curve of the equivalent north gyro

圖4 等效天向陀螺漂移Fig 4 Drift curve of the equivalent up gyro

傳統的分析方法是對等效漂移在一個周期內累加，只要等效陀螺漂移累加和為零，就表示旋轉方案實現了對器件誤差的旋轉調制［7，8］。但對圖2～圖4的等效漂移曲線進行分析可知，即使在一個旋轉周期內三軸漂移的累積和為零，但對于不同的旋轉時間tr和停止時間ts，等效漂移的變化規律是不同的，其對慣導系統誤差的影響也是不相同的。

2 雙軸旋轉方案的定位誤差分析

2.1 基于傅里葉級數變換的定位誤差推導

對于雙軸旋轉方案的定位誤差分析，采用先對漂移做拉氏變換代入誤差方程，而后進行拉氏反變換得到時域表達式的方法，其求解過程非常繁瑣。為此，首先對等效漂移進行簡化，在不影響調制漂移基本特性的前提下，得到如圖2～圖4中虛線所示的漂移曲線，即將3個方向的等效漂移簡化為方波形式。

根據靜基座下的捷聯式慣導系統誤差方程，可以得到受漂移誤差激勵的系統經緯度誤差表達式為

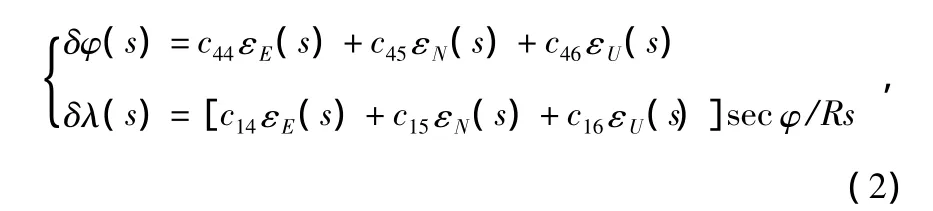
式中 δφ，δλ 分別為緯度誤差和經度誤差，c14～c16與 c44～c46均為已知量［8］。

對于如圖2～圖4所示的等效陀螺漂移，無法直接代入式(2)直接求解經緯度誤差。為此，對簡化后的等效漂移進行傅里葉級數展開，得到

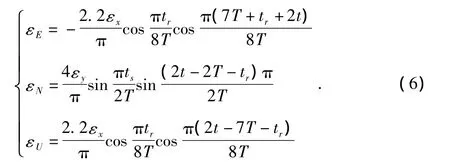
通過對式(6)進行拉氏變換，代入式(2)后通過拉氏反變換運算，即可得到雙軸依次旋轉方案的定位誤差時域表達式。

2.2 不同轉位方式下的定位誤差分析

為分析不同旋轉時間tr和停止時間ts對系統定位誤差的影響，對 tr≈ts，tr?ts和 tr?ts三種情況下的定位誤差進行分析。

1)tr≈ts情況

考慮到旋轉周期8(tr+ts)?Ts(舒勒振蕩周期)，可以簡化得緯度、經度誤差時域輸出為

2)tr?ts情況

簡化后的緯度、經度誤差時域輸出為

3)tr?ts情況

簡化后的緯度、經度誤差時域輸出為

通過對式(7)～式(11)的輸出可以看出:在陀螺漂移的激勵下，緯度誤差和經度誤差中僅包含常值和振蕩誤差項，沒有隨時間增長的趨勢項。而由式(11)可知，當tr?ts時，被激勵緯度和經度誤差已不包含與北陀螺εy有關的誤差項，而且，將式(11)與其他2種情況的誤差項幅值相比，式(11)中的經緯度誤差項幅值遠小于tr≈ts和tr?ts情況下的經緯度誤差幅值。

3 計算機仿真

仿真條件設置如下:

陀螺漂移:εx=0.01°/h，εy=0.01°/h，εz=0.01°/h;

對稱標度因數誤差陣

非對稱標度因數誤差陣

安裝誤差陣

初始位置:φ0=45.78°，λ0=126.6705°;

旋轉周期:取旋轉角速度為3°/s。

1)tr=ts=1 min:系統在每個停止位停留1 min，在2個停止位間旋轉時間為1min，系統定位誤差曲線如圖5所示。

圖5 仿真條件1激勵的定位誤差曲線Fig 5 Positioning error curve excited by simulation condition 1

2)旋轉系統無停止時間，旋轉時間為tr=1 min:系統沒有停止位，在每個改變旋轉軸的位置間旋轉時間為1 min，

式中 εE，εN，εU為沿地理坐標系軸向的等效陀螺漂移，εx，εy，εz為沿 x，y，z陀螺敏感軸的陀螺漂移，T=tr+ts。

考慮到慣導系統為一低通濾波器，為簡化推導分析過程，對簡化后的等效漂移進行傅里葉級數展開，提取其級數展開式頻率最低的基波誤差信號，得到系統定位誤差曲線如圖6所示。

圖6 仿真條件2激勵的定位誤差曲線Fig 6 Positioning error curve excited by simulation condition 2

通過不同轉位方式下的經緯度誤差分析和仿真分析可知:

1)減小系統在停止位停留時間，即慣性測量單元在一個旋轉周期內，旋轉周期長于停止時間，常值漂移激勵的經緯度誤差越小;

2)盡量減小旋轉周期。在雙軸旋轉方案中，常值漂移激勵的經緯度誤差正比于系統旋轉周期，旋轉周期越長，則激勵的經緯度誤差越大。

4 結論

針對雙軸旋轉調制捷聯慣導受旋轉方案影響的問題，對旋轉方案的誤差特性開展了定量推導分析。結合仿真，明確了轉、停時間對系統經緯度誤差的影響關系，在此基礎上給出了轉位方案的優化改進方法，為設計提高雙軸旋轉捷聯慣導經度提供了參考依據。

［1］張炎華，王立瑞，戰興群，等.慣性導航技術的新進展及發展趨勢［J］.中國造船，2008，10(49):134-141.

［2］Tucker L E.The AN/WSN—7B marine gyrocompass/navigator［C］∥ION NTM，2000:348-357.

［3］Hibbard R，Wylie B，Levison E.Sperry marine MK—49，The world’s best ring laser gyro ship’s inertial navigation system［C］∥JSDE Proceedings，1996:35-46.

［4］程建華.光纖陀螺捷聯慣導系統監控技術研究［D］.哈爾濱:哈爾濱工業大學，2009:24-25.

［5］翁海娜，陸全聰，黃 昆，等.旋轉式光學陀螺捷聯慣導系統的旋轉方案設計［J］.中國慣性技術學報，2009，17(1):8-17.

［6］孫 楓，孫 偉，郭 真.基于IMU旋轉的捷聯慣導自補償方法［J］.儀器儀表學報，2009，30(12):2511-2517.

［7］袁保倫.四頻激光陀螺旋轉式慣導系統研究［D］.長沙:國防科學技術大學，2007:56-67.

［8］袁保倫，饒谷音.光學陀螺旋轉慣導系統原理探討［J］.國防科技大學學報，2006，28(6):76-80.

［9］張樹俠，孫 靜.捷聯式慣性導航系統［M］.北京:國防工業出版社，1992:55-60.

［10］Wang Xinzhe，Zhao Lin.The research on rotation self-compensation scheme of strapdown inertial system［C］∥ICMA，2009:4760-4764.