基于靈敏度和特異度任意賦權的廣義標準化診斷符合率*

南方醫科大學公共衛生與熱帶醫學學院生物統計學系(510515) 李丹玲 陳平雁

自 Yerushalmy(1947)〔1〕提出靈敏度(SEN)和特異度(SPE)以來，它們一直是評價診斷試驗最基本和最重要的兩項指標。由于靈敏度和特異度是一對互為矛盾的指標，即對于某一診斷方法，一者的增大必定以另一者的減小為代價，反之亦然;所以在不同診斷方法進行比較時，一者的靈敏度較高而另一者的特異度較高時，難以對其做出綜合評價。于是結合靈敏度和特異度的綜合評價指標由此產生，如標準化診斷準確率或標準化診斷符合率。然而，此類綜合評價指標又產生了新的問題，當靈敏度和特異度的重要性不同時，它們就不能反映診斷的真實價值〔2〕。為此，我們將在基于靈敏度和特異度特意賦權的基礎上建立一種新的診斷試驗評價指標－廣義標準化診斷符合率。

廣義標準化診斷符合率的構建

兩種試驗診斷某種疾病的結果用表1和表2表達，縱標目是以“金標準”或稱參照標準確診的受試個體是“患者”(D+)或“非患者”(D－);橫標目為診斷方法所判定的結果“陽性”(T+)或“陰性”(T－)。

表1 甲試驗診斷某疾病的結果

筆者曾提出，兩樣本病例組構成不同時，不宜用診斷符合率檢驗，而應該用標準化診斷符合率檢驗〔3〕。為便于應用，我們將兩樣本的合并人群定義為標準人群。下面導出合并兩樣本為標準人群的標準化診斷符合率檢驗公式。由表3可知，病例組的合計為n1+m1，甲靈敏度為SEN1，預期的真陽性數為(n1+m1)·SEN1，乙靈敏度為SEN2，預期的真陽性數為(n1+m1)·SEN2。對照組的合計為n2+m2，甲的特異度為SPE1，預期的真陰性數位(n2+m2)·SPE1，乙的特異度為SPE2，預期的真陰性數位(n2+m2)·SPE2。由直接法求得標準化診斷符合率:

表2 乙試驗診斷某疾病的結果

表3 標準化診斷符合率計算表

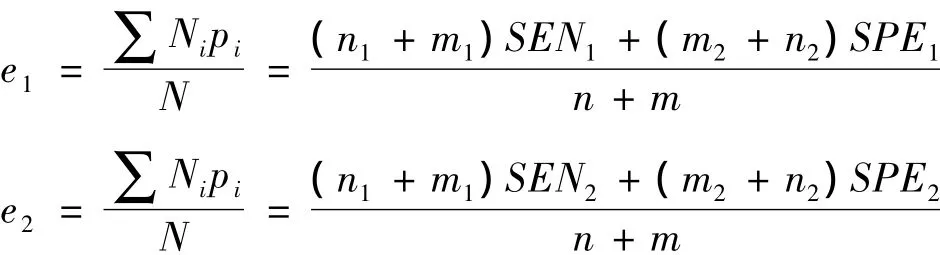
從上，我們得知，標準化診斷符合率其實質是靈敏度與特異度的一個線性組合，我們在基于靈敏度和特異度任意賦權的基礎上建立廣義標準化診斷符合率。

廣義標準化診斷符合率的構建遵循如下兩原則:

(1)靈敏度、特異度的權重之和為1，即靈敏度的權重為w，特異度的權重為1-w;

(2)滿足特殊性。當靈敏度和特異度同等重要時，即權重均為0.5時，廣義標準化診斷符合率e'等于標準化診斷符合率e。

因此我們構造出來的廣義標準化診斷符合率有如下形式:

其中0≤w≤1。

廣義標準化診斷符合率的統計推斷

根據中心極限定理，當樣本量較大時，檢驗統計量

其中Se1'－e2'是兩種診斷試驗的廣義標準化診斷符合率之差的標準誤。為求之，我們先計算其近似方差，由于兩診斷試驗相互獨立，因而有:

至此，兩個獨立診斷試驗的廣義標準化診斷符合率比較的統計推斷方法得以建立:

這里，Z～N(0，1)。

檢驗統計量Z為權重w的單調函數

筆者通過理論證明得知權重w對Z的影響如下:

(1)若 SEN1≤SEN2，SPE1≥SPE2，則隨著 w 的增大，Z減小(當且僅當 SEN1=SEN2，SPE1=SPE2時，Z≡0);

(2)若 SEN1＜SEN2，SPE1＜SPE2，則隨著 w 的增大，Z先減小后增大，最小值點為

假想的兩獨立診斷試驗的結果分別列于表4，試比較之。

分析結果見表4，若靈敏度的權重取0.4(特異度的權重為0.6)，兩法的e'分別為0.577和0.661，兩法的診斷價值無統計學差異(Z=－1.445，P=0.148);當靈敏度和特異度取相同權重時，即w=0.5時，此時廣義標準化診斷符合率等于標準化診斷符合率(e)，乙法的診斷價值高于甲法(Z=－2.722，P=0.006)。若靈敏度的權重取0.6(特異度的權重為0.4)，兩種檢驗方法的e'分別為0.519和0.745，乙的診斷價值高于甲法(Z= －3.909，P ＜0.001)。

(3)若 SEN1≥SEN2，SPE1≤SPE2，則隨著 w 的增大，Z增大;

(4)若 SEN1＞SEN2，SPE1＞SPE2，則隨著 w 的增大，Z先增大后減小，最大值點w0同上。我們通過舉例來演示上述四種不同情況下Z如何隨w的變化而變化(見圖1)。

〔實例〕

討 論

表4顯示，乙法的靈敏度高于甲法，但其特異度低于后者。此類資料若分別比較靈敏度或特異度顯然難以做出一個完整的判斷，需要用類似標準化診斷符合率這樣的綜合指標進行評價，這正是標準化診斷符合率的優勢所在。

圖1 檢驗統計量Z為權重w的單調函數

表4 三種不同權重時廣義標準化診斷符合率檢驗的結果

關于靈敏度和特異度的相對重要性，Galen和Gambino曾有論述〔4〕:(1)對病情嚴重但治療有積極意義，漏診會造成不可挽回的損害而誤診不治帶來嚴重后果的疾病，如嗜鉻細胞瘤，以靈敏度較為重要;(2)對病情重又屬于不治之癥，誤診會產生嚴重后果的疾病，如多發性硬化癥，以特異度較為重要;(3)對病情較重但治療有積極意義，漏診和誤診造成危害相當的疾病，如心肌梗塞、糖尿病、某些血液病等，靈敏度和特異度大致同等重要。Galen和Gambino提出的上述概念可看作臨床應用的一般原則，尚不具備技術上的可操作性。本研究所建立的方法可以量化地體現兩者的相對重要性，而且其意義更為直觀。

靈敏度和特異度權重的確定是廣義標準化診斷符合率應用的一個核心問題，應該由相關研究領域的專家根據其專業知識、臨床經驗、同行共識給出答案。當廣義標準化診斷符合率的應用更為廣泛的時候，meta分析等數據處理手段也可提供輔助手段。

相對于標準化診斷符合率，廣義標準化診斷符合率不僅允許靈敏度和特異度任意賦權，而且更滿足特殊性，當靈敏度和特異度等權時(均為0.5)，廣義標準化診斷符合率等價于標準化診斷符合率，當SEN1=SEN2=1或SPE1=SPE2=1時，Z恒為常數。

試驗樣本中的病例組構成是診斷試驗推斷方法面臨的一個普遍問題，本研究結果將對于其他評價方法產生很好的啟示作用。

1．Yerushalmy J．Statistical problems in assessing methods of medical diagnosis，with special reference to x-ray techniques．Public Health Reports，1947，62:1432-1449．

2．陳平雁．診斷試驗的評價指標及其應用．中國衛生統計，1991，8(5):53-57．

3．陳平雁，郭祖超，胡琳．比較兩種診斷試驗的統計方法．中國衛生統計，1990，7(2):22-26．

4．Galen RS，Gambino SR．Beyond normality:the predictive value and efficiency of medical diagnosis．New York:Jonewiley，1975，50-53．

5．Christensen E．Methodology of diagnostic tests in hepatology．Ann Hepatol，2009，8(3):177-183．

6．Reitsma JB，Glas AS，Rutjes AW，et al．Bivariate analysis of sensitivity and specificity produces informative summary measures in diagnostic reviews．J Clin Epidemiol，2005，58(10):982-990．

7．Van den Bruel A，Cleemput I，Aertgeerts B，et al．The evaluation of diagnostic tests:evidence on technical and diagnostic accuracy，impact on patient outcome and cost-effectiveness is needed．J Clin Epidemiol，2007，60(11):1116-1122．